Original: https://zhuanlan.zhihu.com/p/643560252
I also had the almost universal question: how is this achieved? Does the potential of silicon-based intelligence far exceed that of carbon-based intelligence?
In this article, I do not attempt to explain everything about ChatGPT, but rather, I will start from the principles to think about the key elements of computer understanding of language, focusing on a specific entry point — embedding — something that is difficult to understand at first glance but is extremely critical.
This article is completed by an outsider through amateur research and fragmented thoughts, and errors are inevitable; I welcome corrections from professional researchers.
1 Encoding: Digitization of Text
The term embedding translates to Chinese as: 嵌入, which is a frustrating term — what is embedding? What is embedded? What does it have to do with natural language?
Embedding is represented as a fixed-length array, or vector, but what exactly is it? Why do we need it? What role does it play in the process of computer understanding of natural language?
To answer these questions, let’s first consider: what do we need to do for a computer to understand natural language?
The basis of computation is numbers, while natural language is text. Thus, it is easy to think that the first step is to digitize text; for convenience, we will call this process encoding. To design encoding methods, we naturally need to consider: what properties must the encoding rules satisfy?
One property can be clearly stated:
Property 1: Each word must have a unique quantitative value, and different words must have different quantitative values.
The logic behind this is self-evident: one word many meanings, or many words one meaning, will increase the difficulty of computer understanding of language, just like homophones or polysemous words pose difficulties for humans. Although human intelligence allows us to overcome these obstacles, it is clearly necessary to lower some difficulties for computers that are still in the stage of developing intelligence.
It is very easy to design a method that satisfies Property 1; for example: first exhaust all human characters or phrases — this set must be finite, for example, there are 100,000 Chinese characters, about 600,000 words in the dictionary, and there are 26 letters, with fewer than 1 million English words — since it is a finite set, we can assign a fixed number to each word.
For example, opening a dictionary, we can assign a different numerical value to each word encountered:
A --> 1
Abandon --> 2
Abnormal --> 3
...
This completes the encoding that satisfies Property 1. For example, the phrase “Hello World” can be input as a numerical sequence like “3942 98783”, allowing it to be processed by the computer.
However, the problem with this method is obvious:
The numerical values are disconnected from the meanings of the words.
What problems can this disconnection cause? We can think through a simple example: in English, a and an are completely homogenous words, while a and abnormal are vastly different words. If we assign the value 1 to a and the value 2 to abnormal, while assigning 123 to an, we may find that a and abnormal seem closer in numerical value, while a and an, two homogenous words, are far apart. This leads us to consider adding another property to ensure that the numerical values correlate with the meanings:
Property 2: Words with similar meanings need to have “close” quantitative values; words with dissimilar meanings need to be as “far apart” as possible.
2 Meaning-Based Encoding
Although the previous example mentioned that dictionary encoding methods disconnect numerical values from meanings, it did not explain why numerical values and meanings should be correlated — intuitive thinking may suggest this is obvious, but the vague is often buried beneath a logic that deserves clarity. I can think of two reasons:
-
It can help more efficiently understand semantics;
-
It allows for greater freedom in the design of computational models.
How do we understand the first point? If the numerical distribution of words is unrelated to their meanings, it will make the sequence of texts overly random. For example:
Sentence 1: Zhang San is speaking. Sentence 2: Li Si is giving a speech.
These two sentences have strong homogeneity, but if the encoding of words does not meet Property 2, it will lead to significant differences in the sequence features of the two sentences. The following examples may be sufficiently intuitive:
If synonyms have close quantitative values, the relationship between words and values might look like this:
Zhang --> 105, Li --> 99
San --> 3, Si --> 4
is --> 200,
speaking --> 300, giving a speech --> 295
And if synonyms have dissimilar quantitative values, the relationship might look like this, seemingly unrelated:
Zhang --> 33, Li --> 1
San --> 5, Si --> 200
is --> 45,
speaking --> 2, giving a speech --> 42
In other words, when Property 2 is satisfied, semantically similar sentences will be closer in sequence features, which will help the computer understand commonalities and distinguish characteristics more efficiently; conversely, it will create many difficulties for the computer. Difficulty in capturing commonalities between homogeneous content means that the model will require more parameters to describe the same amount of information, making the learning process evidently more challenging. Jack Rae from OpenAI mentioned a profound perspective on understanding language models in a presentation at Stanford:
-
A language model is a compressor.
This perspective has been explained in many articles.
All compression can generally be summarized within the following framework: extract commonalities, retain individuality, filter noise. Viewing this from this perspective makes it easier to recognize the necessity of Property 2. The numerical values encoded for different words, whether based on the similarity of meanings, will directly impact the compression efficiency of the language model regarding input data.
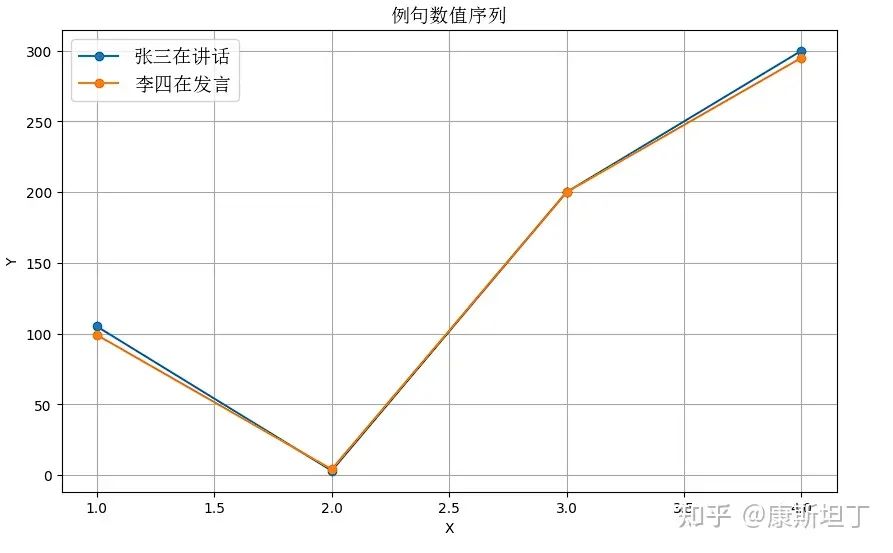
Encoding values not based on meaning clustering
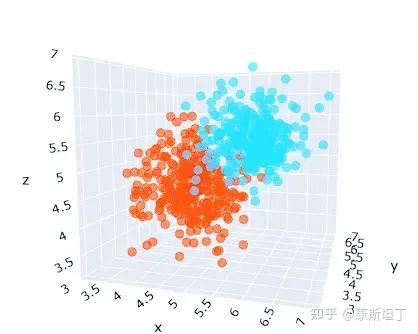
Encoding values based on meaning clustering
How do we understand the second point?
Because words are discretely distributed, and the output of computational models — unless using very simple operations and constraining parameter weights — is difficult to exactly match defined quantitative values.
For neural network models, each node and each layer must be continuous; otherwise, gradients cannot be calculated, and backpropagation cannot be applied. The combination of these two facts may lead to the situation where the quantitative values of words can all be integers, but the output of the language model does not have to be. For example, when the model outputs 1.5, and the vocabulary only defines 1 and 2, how should we handle this?
We would hope that both 1 and 2 could be applicable, and even 3 might not be too outrageous, so the words represented by 1 and 2 should ideally have some commonality in meaning, rather than having no apparent connection like “a” and “abandon”. When similar words cluster together, the probability of inferring effective outputs increases.
Image source: https://en.wikipedia.org/wiki/Generative_pre-trained_transformer
—— Understanding this, the last layer of the GPT model becomes very easy to comprehend. Before the last layer, the reasoning object is represented in vector form, and the output is a “fuzzy” vector representing semantics. Here, “fuzzy” means this vector may not correspond to any known word.
Therefore, the entire model needs to make a final inference, based on the semantic information contained in this “fuzzy” vector, to find the word in the vocabulary that best matches these features to serve as the actual output. In the transformer, the final output is a probability distribution representing the probability of each word matching this “fuzzy” vector.
Now we know that Property 2 is necessary; is it possible to salvage the dictionary encoding method based on this consideration? For example… find a thesaurus and assign similar values to similar words?
The problem quickly arises: if A and B have similar meanings, and B and C have similar meanings, it does not necessarily mean A and C have similar meanings.
For example:
A = "Love", B = "Passion", C = "Rage"
A = "Comedy", B = "Play", C = "Game"
In these two cases, A and B are close, B and C are also close, but A and C are not. Where does the problem lie?
-
The multidimensionality of meanings.
When using a scalar to represent a word, the relationship between words can only be derived from the difference between two scalars, resulting in only two states: “far” and “near”; but the reality may be that two words are only close in certain dimensions. For example, “Love” and “Passion” are close in emotional intensity, both indicating strong emotions, but in terms of emotional color — whether it is negative or positive — passion has a more neutral tone, so similarly intense “Rage” is also close to “Passion”, but its emotional color is negative.
Thus, we need a multidimensional numerical representation, and it is natural to think of using vectors — for each word, we can express it as a group of numbers rather than a single number; this way, we can define proximity in different dimensions, and the complex relationships between words can be expressed in this high-dimensional space — this is embedding, and its significance is self-evident. The term “embedding” is a poor choice; it would be better to call it “word meaning vector”; and the space where word meaning vectors exist can be referred to as “semantic space”.
3 How to Design an Encoder
So far, we have found a digital form that can express word meanings — vectors — and we know the properties that a good encoding method should satisfy. The final question is how to design a method to achieve our desired encoding.
A relatively easy method to think of is to correlate the different dimensions of word meanings with different dimensions of the vector. For example, comprehensively breaking down the dimensions of word meanings: nounness, verbeness, adjectiveness, quantity characteristics, characters, active, passive, emotional color, emotional intensity, spatial up and down, spatial front and back, spatial inside and outside, color characteristics, … As long as the number of dimensions is sufficient, it should encompass all the information contained in the meanings of words; once we define each dimension, we can assign values to each word in the corresponding dimensions, thus completing the vectorization of words and perfectly satisfying the above two properties. However, this seemingly feasible design lacks practicality.
First, to encompass all dimensions of meanings, the number of dimensions must be extremely high, and finely segmenting word meanings is very difficult. Even if segmented, assigning effective values to each dimension of different meanings for each word would be challenging even for seasoned linguists. Today, none of the well-known language models have vectorized words in this way. However, this conceptual approach is meaningful; the different dimensions of word meaning vectors for computers are akin to the dimensions we listed above — word type, quantity, time, space, etc. — for humans.
Purely constructed methods are not feasible; today we already know an effective solution: neural networks and big data create miracles. This paradigm originated with Word2Vec. Today, language models are all based on word meaning vectors, and the effective use of word meaning vectors truly began with Word2Vec.
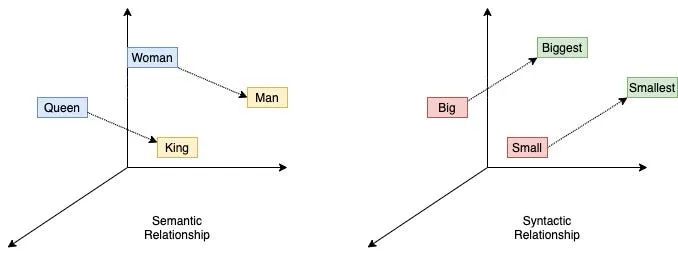
The key to Word2Vec is an important insight, a highly enlightening perspective:
The meaning of a word can be defined by the context in which it appears.
This can also be expressed as: Words with similar contexts must also have similar meanings. Doesn’t this make sense? This viewpoint was proposed by linguist Zellig Harris in 1954, and has since been widely accepted. The two approaches of Word2Vec are:
Center word –> Neural network –> Context
Context –> Neural network –> Center word
Looking back today, this work was destined for success from the start: Principally, it is based on the widely accepted “Distribution Hypothesis”; methodologically, it employs a powerful fitting neural network model; and most importantly, there is an abundance of data.
This method is certainly not the endpoint; its limitations are apparent — but its pioneering nature is sufficient — it only utilizes and extracts the shallow structure of the “Distribution Hypothesis”. How to understand this statement?
Essentially, Word2Vec does not attempt to understand the semantics within sentences. Therefore, for identical contexts, the semantic similarity of different center words is easily captured; as the clustering of word meaning vectors gradually forms, contexts formed by synonyms can also somewhat label center words with similar meanings. However, human language structure is very complex; when identical semantics are expressed through different sentence structures, voices, and rhetoric, certain synonym pairs may be deeply buried.
Consider this example given by ChatGPT:
Sentence 1: Driven by an insatiable thirst for knowledge, she stayed late every night, her eyes dancing across the pages of books as if they were starry skies. Sentence 2: Isn’t it unusual, that she, prompted by an unquenchable intellectual curiosity, burns the midnight oil, pouring over pages as though navigating constellations?
Both sentences describe a woman reading late at night, driven by an endless thirst for knowledge. There are many pairs of words with similar meanings in both sentences, but without understanding semantics, the similarities between these pairs of words are difficult to identify.
Next, we can discuss GPT.
It is a model capable of understanding sentences. If we say that the models discussed earlier, like Word2Vec, are teaching computers to “recognize words”, then the training of the GPT model is a process of “recognizing words” + “reciting”. The teacher ultimately only tests how well the book is recited, but to recite well, GPT has also passively strengthened its word recognition ability.
The core of reasoning is the transformer, and the core of the transformer is the attention mechanism. What is the attention mechanism?
In summary: after calculating the “distance” between word meaning vectors, more attention is paid to words that are close in distance, and the meanings of words receiving high attention gain higher activation values. When the prediction is completed, through the backpropagation algorithm: when specific activations assist the final prediction, the associations between corresponding words will be strengthened; conversely, they will be weakened, and the model learns the relationships between words in this way. Thus, from the perspective of the “Distribution Hypothesis”, recognizing words essentially means understanding the relationships between a word and other words. This forms a structure where recognizing words aids in reciting, and reciting helps in recognizing words. Here, I would like to extract a personal viewpoint:
One reason the attention mechanism is important and effective is that it can effectively assist in clustering word meaning vectors (embedding).
Interestingly, the example of GPT illustrates a common engineering thought process: breaking down large problems into smaller ones and solving them one by one, just as the article begins with the question:
What do we need to do for a computer to understand natural language?
The basis of computation is numbers, while natural language is text. Thus, it is easy to think that the first step is to digitize text…
This statement implies a problem-solving path: first digitize text, then consider the problem of understanding sentences. The interesting part is that the best method for vectorizing words is to directly train a language model that understands sentences; it’s like training a baby to run instead of walk. Humans may fall and get hurt, but machines won’t — at least not before they are embodied — so the step-by-step learning process established by humans to reduce costs may not be suitable for artificial intelligence — and it is not difficult to find that many good solutions in deep learning are often one-step solutions.
4 Conclusion
This article has introduced my understanding of embedding in language models. However, embedding is not limited to this.
Images can have embeddings, sentences and paragraphs can also have embeddings — essentially, they all express meaning through a set of numbers. The embedding of paragraphs can serve as an efficient index for semantic-based searches, and behind AI painting technology, there is an interaction of these two types of embeddings — in the future, if there is a unified multimodal model, embedding will undoubtedly be one of its cornerstones and bridges.
The wave of the era brought about by AI is undoubtedly approaching, and today is a moment still difficult to see clearly into the future. One of the few things we can do now is to keep learning. I hope this article can help you who are learning.
Editor / Zhang Zhihong
Reviewer / Fan Ruiqiang
Recheck / Zhang Zhihong
Click below
Follow us