
Source: New Intelligence[ Introduction ] Recently, researchers from Tsinghua University and Ant Group re-examined the application of the Transformer structure in time series analysis, proposing a completely new inverted perspective—achieving comprehensive leadership in time series prediction tasks without modifying any modules!
In recent years, Transformers have made continuous breakthroughs in natural language processing and computer vision tasks, becoming the foundational model in the deep learning field.
Inspired by this, numerous Transformer model variants have been proposed in the time series domain.
However, an increasing number of recent studies have found that using simple prediction models based on linear layers can achieve better results than various modified Transformers.

Recently, in response to doubts about the effectiveness of Transformers in the field of time series prediction, the machine learning laboratory of the Tsinghua University Software School and scholars from Ant Group collaborated to publish a time series prediction work, which sparked heated discussions on forums like Reddit.
In this work, the authors proposed the iTransformer, which considers the data characteristics of multi-dimensional time series, not modifying any Transformer modules, but breaking conventional model structures to achieve comprehensive leadership in complex time series prediction tasks, attempting to address the pain points of Transformer modeling for time series data.

With the support of iTransformer, Transformers have achieved a comprehensive turnaround in time series prediction tasks.
Background of the Problem
Real-world time series data is often multi-dimensional, including not only the time dimension but also variable dimensions.
Each variable can represent different observed physical quantities, such as multiple meteorological indicators (wind speed, temperature, humidity, pressure, etc.) used in weather forecasting, or can represent different observed subjects, such as the hourly power generation of different equipment in a power plant.
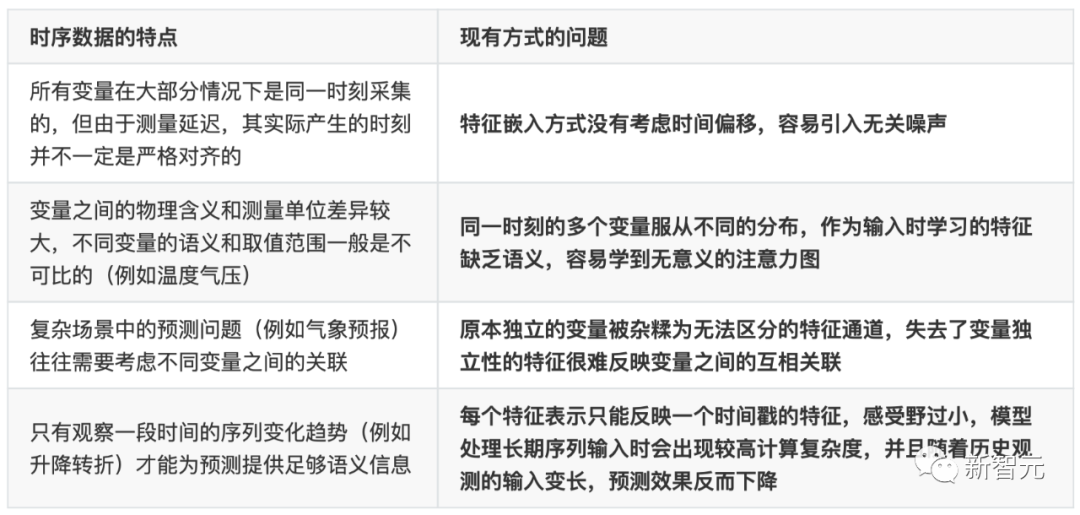
Generally, different variables have completely different physical meanings, and even if the semantics are the same, their measurement units may be completely different.
Previous Transformer-based prediction models typically first embed multiple variables at the same moment into high-dimensional feature representations (Temporal Tokens), using feed-forward networks to encode the features of each moment, and using attention modules to learn the interrelations between different moments.
However, this approach may have the following issues:
Design Philosophy
Unlike natural language where each word (Token) has strong independent semantic information, in time series data, each “word” (Temporal Token) seen from the existing Transformer perspective often lacks semantics and faces issues like timestamp misalignment and small receptive fields.
In other words, the modeling capability of traditional Transformers for time series has been greatly weakened.
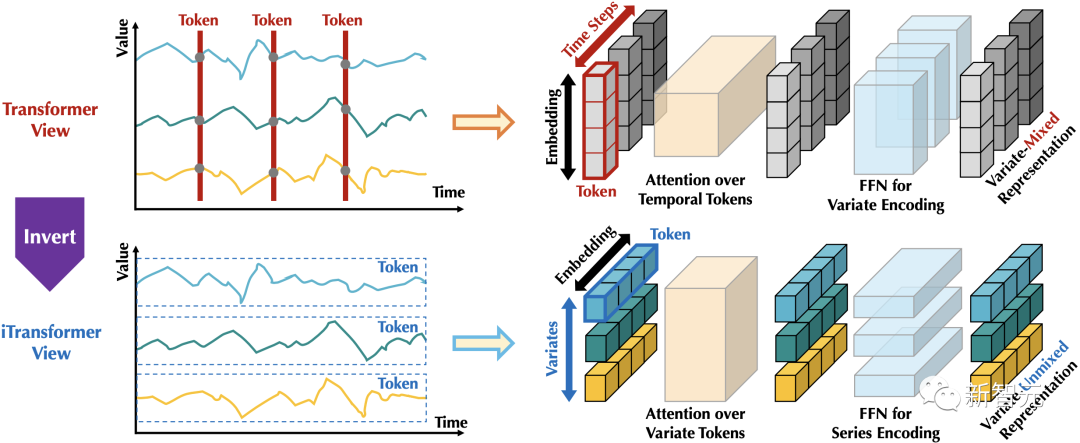
To address this, the authors proposed a completely new inverted perspective.
As shown in the figure below, by inverting the original modules of the Transformer, the iTransformer first maps the entire sequence of the same variable into high-dimensional feature representations (Variate Tokens), with the resulting feature vectors describing the variables independently, characterizing their historical processes.
Subsequently, the attention module can naturally model the correlations between variables (Multivariate Correlation), while the feed-forward network encodes the features of historical observations layer by layer in the time dimension and maps the learned features to future predictions.
In contrast, the layer normalization (LayerNorm), which has not been deeply explored in time series data, will also play a crucial role in eliminating distribution differences between variables.
iTransformer
Overall Structure
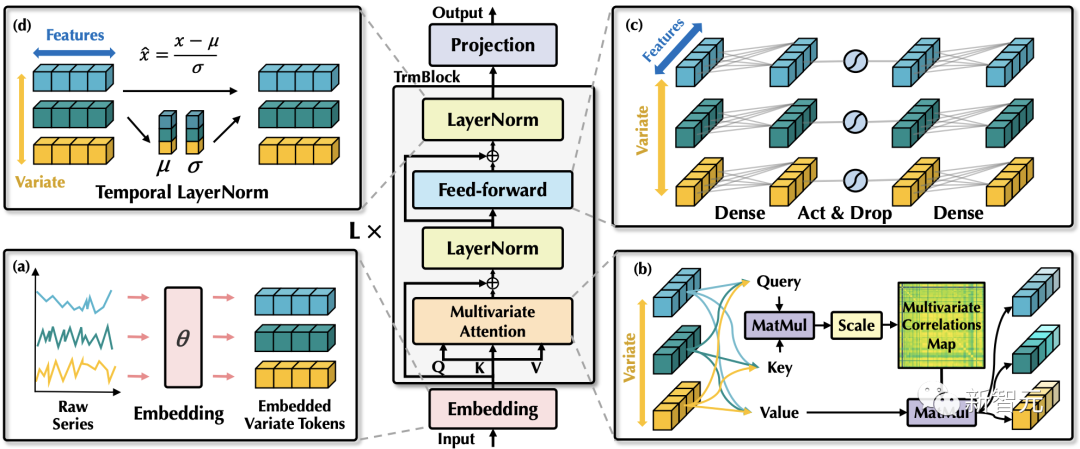
Unlike the more complex encoder-decoder structure used in previous Transformer prediction models, the iTransformer only contains an encoder, including an embedding layer (Embedding), a projection layer (Projector), and stackable Transformer modules (TrmBlock).
Modeling Variable Feature Representations
For a multi-dimensional time series with a time length of and a variable count of , the article uses to represent all variables at the same moment, and to represent the entire historical observation sequence of the same variable.
Considering that has stronger semantics and relatively consistent measurement units than , unlike previous methods of embedding features into , this method uses the embedding layer to independently map features for each , obtaining feature representations for variables, which contain the temporal changes of the variables over the past time.
This feature representation will undergo self-attention mechanisms in each layer of the Transformer modules, first facilitating information exchange between variables, normalizing the feature distributions of different variables through layer normalization, and then performing fully connected feature encoding in the feed-forward network. Finally, it will be mapped to prediction results through the projection layer.
Based on the above process, the implementation of the entire model is very simple, and the calculation process can be represented as:
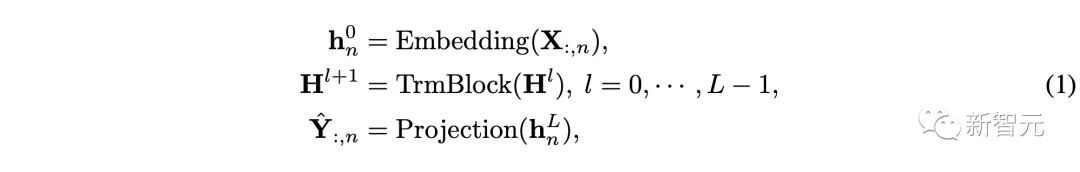
where is the predicted result corresponding to each variable, and both the embedding layer and projection layer are implemented based on multi-layer perceptrons (MLP).
It is worth noting that because the order between time points is already implicitly contained in the arrangement order of the neurons, the model does not need to introduce position encoding (Position Embedding) from the Transformer.
Module Analysis
After reversing the dimensions of the Transformer module for processing time series data, this work re-examines the responsibilities of each module in the iTransformer.
1. Layer Normalization:Layer normalization was originally proposed to improve the stability and convergence of deep network training.
In previous Transformers, this module normalized multiple variables at the same moment, making each variable indistinguishable. Once the collected data is not time-aligned, this operation will also introduce non-causal or delayed process interaction noise.
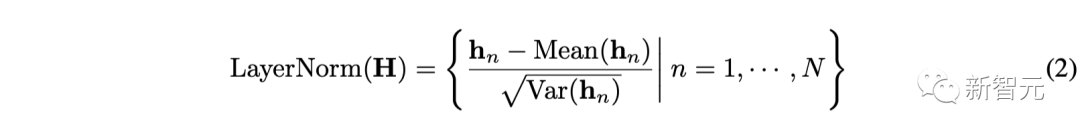
In the inverted version (as shown in the formula above), layer normalization is applied to the feature representations of each variable (Variate Tokens), allowing all variable feature channels to be under a relatively uniform distribution.
This normalization idea has been widely proven effective in handling non-stationary time series problems, and in the iTransformer, it can be naturally achieved through layer normalization.
Moreover, since all variable feature representations are normalized to a normal distribution, the differences caused by varying ranges of variable values can be mitigated.
In contrast, in the previous structure, the feature representations (Temporal Tokens) of all timestamps would be uniformly standardized, resulting in the model seeing a smoothed time series.
2. Feed-Forward Network:The Transformer uses feed-forward networks to encode word vectors.
In previous models, the “word” vectors formed were multiple variables collected at the same time, whose generation times may not be consistent, and it is difficult for a “word” reflecting a time step to provide sufficient semantics.
In the inverted version, the “word” vectors are formed from the entire sequence of the same variable. Based on the universal representation theorem of multi-layer perceptrons, it has sufficiently large model capacity to extract time features shared in historical observations and future predictions, and use feature extrapolation for prediction results.
Another basis for modeling the time dimension using feed-forward networks comes from recent research, which found that linear layers excel at learning time features inherent to any time series.
In this regard, the authors proposed a reasonable explanation: the neurons of linear layers can learn how to extract intrinsic properties of arbitrary time series, such as amplitude, periodicity, and even frequency spectrum (the Fourier transform is essentially a fully connected mapping on the original sequence).
Therefore, compared to the previous approach of using attention mechanisms to model temporal dependencies, using feed-forward networks is more likely to achieve generalization on unseen sequences.
3. Self-Attention:The self-attention module in this model is used to model the correlations between different variables, which is extremely important in complex prediction scenarios driven by physical knowledge (e.g., weather forecasting).
The authors found that each position in the self-attention map (Attention Map) satisfies the following formula:
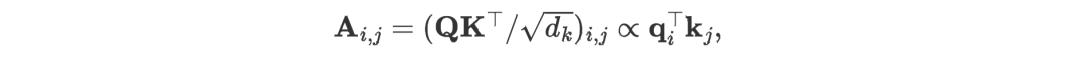
where corresponds to the Query and Key vectors of any two variables. The authors believe that the entire attention map can reveal the correlations between variables to some extent, and in the subsequent weighted operations based on the attention map, highly correlated variables will receive greater weights in their interactions with their Value vectors, making this design more natural and interpretable for modeling multi-dimensional time series data.
In summary, in the iTransformer, layer normalization, feed-forward networks, and self-attention modules consider the characteristics of multi-dimensional time series data itself, and the three work systematically together, achieving an effect of 1+1+1 > 3.
Experimental Analysis
The authors conducted extensive experiments on six major multi-dimensional time series prediction benchmarks and performed predictions on the online service load prediction task data (Market) from the Alipay trading platform.
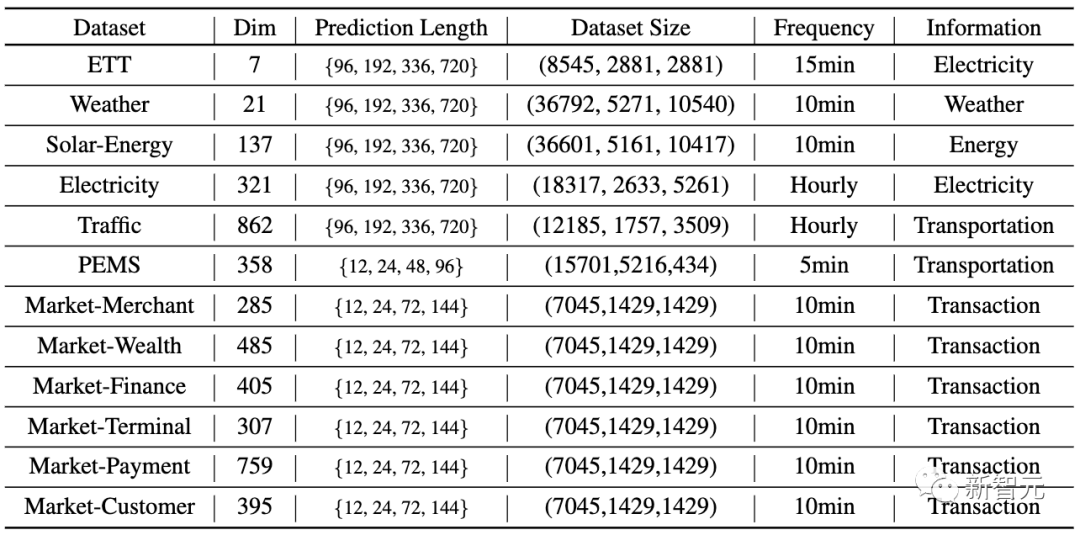
The experimental section compared 10 different prediction models, including representative Transformer models in the field: PatchTST (2023), Crossformer (2023), FEDformer (2022), Stationary (2022), Autoformer (2021), Informer (2021); linear prediction models: TiDE (2023), DLinear (2023); TCN models: TimesNet (2023), SCINet (2022).
Moreover, the article analyzes the gains brought by module inversion to numerous Transformer variants, including general performance improvements, generalization to unknown variables, and better utilization of historical observations.
Time Series Prediction
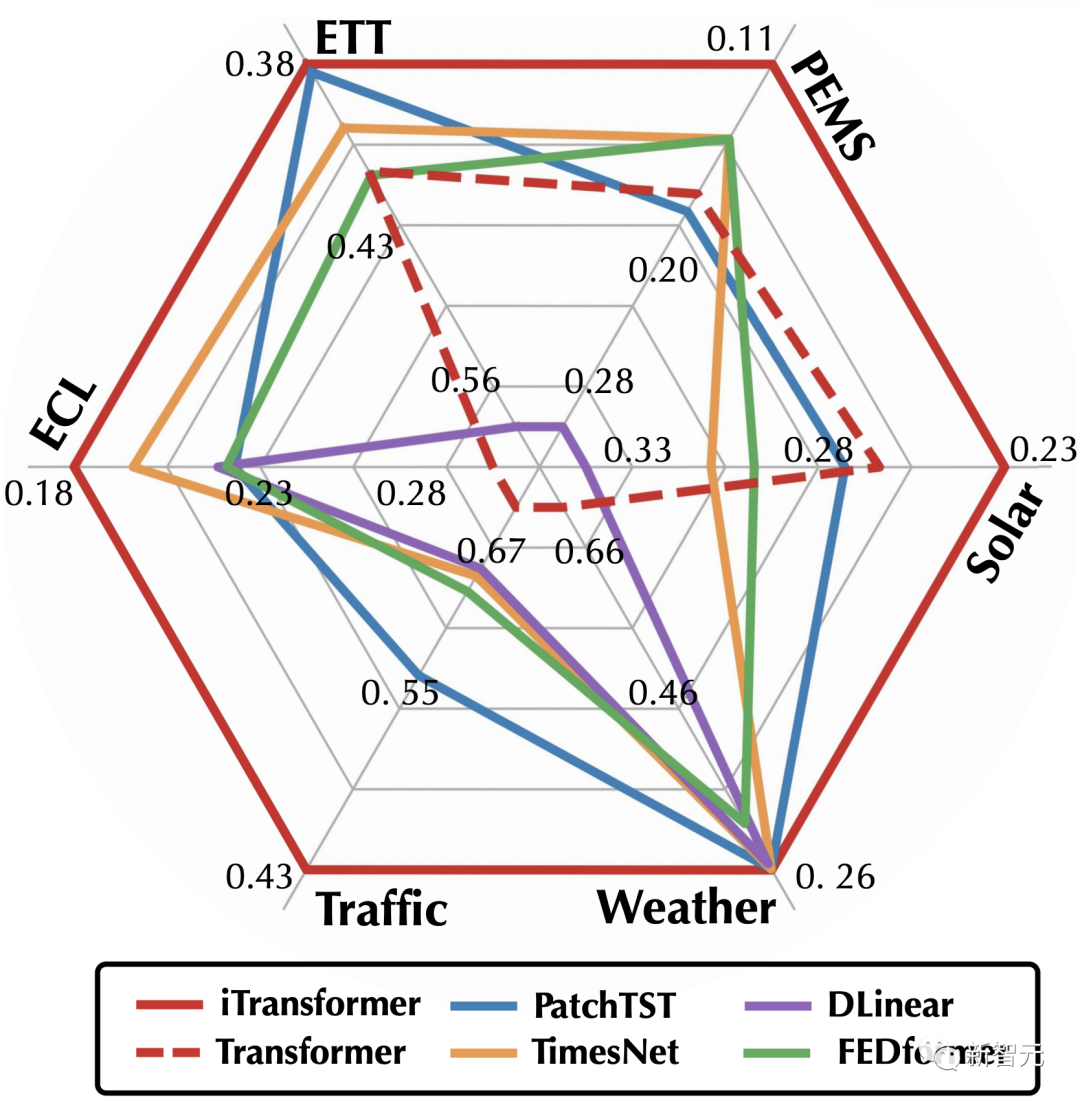
As shown in the radar chart at the beginning, the iTransformer achieved SOTA in all six test benchmarks and achieved optimal results in 28 out of 30 scenarios in the Market data (see the paper appendix for details).
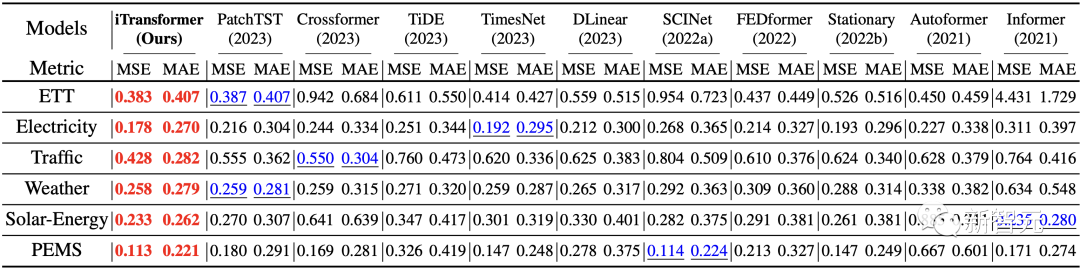
In the challenging scenario of long-term prediction and multi-dimensional time prediction, the iTransformer has comprehensively surpassed recent prediction models.
Generality of the iTransformer Framework
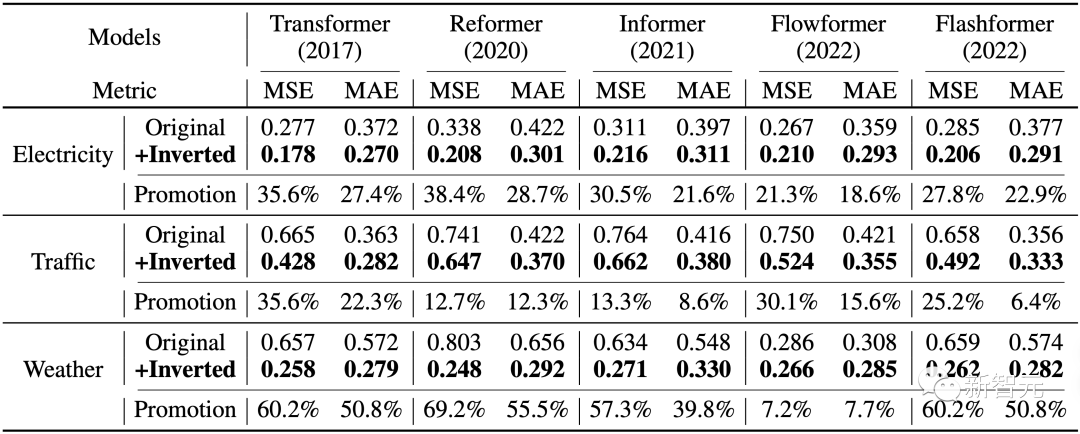
While achieving optimal results, the authors conducted comparative experiments on various Transformer variants such as Reformer, Informer, Flowformer, and Flashformer, proving that the inversion is a structure framework that better aligns with the characteristics of time series data.
1. Improved Prediction Performance
By introducing the proposed framework, these models have achieved significant improvements in prediction performance, demonstrating the universality of the core ideas of iTransformer and the feasibility of benefiting from advances in efficient attention research.
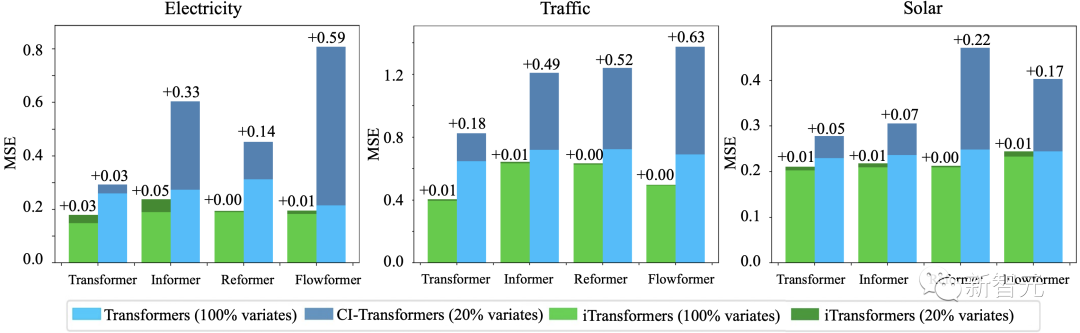
2. Generalization to Unknown Variables
Through inversion, the model can input a different number of variables during inference compared to training. The article compares this with a generalization strategy—Channel Independence—and the results show that this framework can still minimize generalization error while using only 20% of the variables.
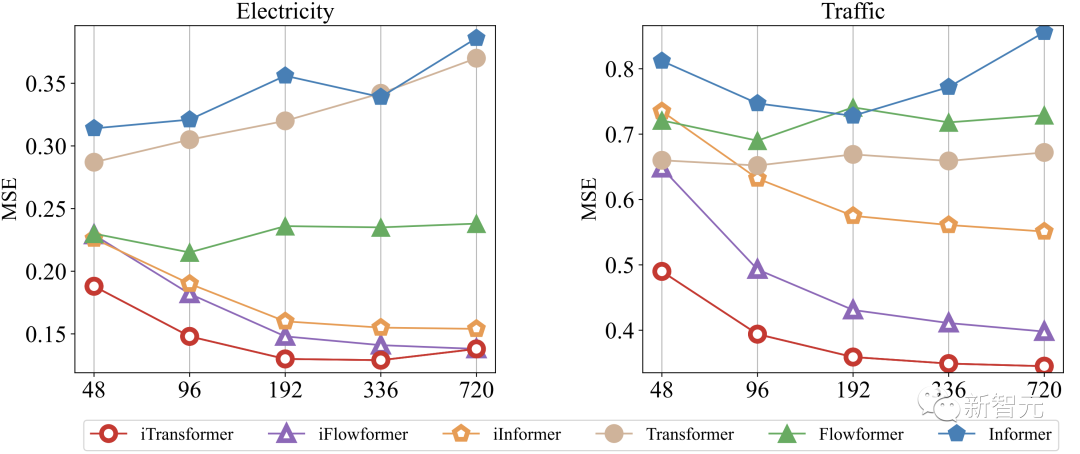
3. Using Longer Historical Observations
Previous Transformer-based models may not necessarily improve their prediction performance as the length of historical observations increases. The authors found that after using this framework, the model exhibited an astonishing trend of reduced prediction errors with increased historical observations, partially validating the rationality of module inversion.
Model Analysis
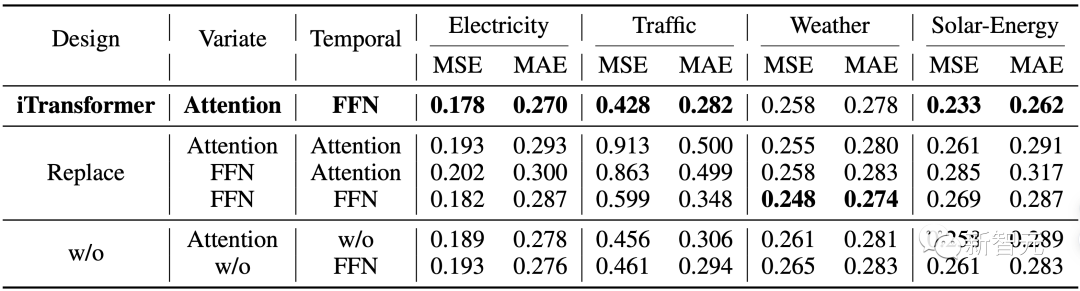
1. Model Ablation Experiments
The authors conducted ablation experiments to verify the rationality of the iTransformer module arrangement.
The results indicate that using self-attention in the variable dimension and linear layers in the time dimension achieves optimal performance across most datasets.
2. Feature Representation Analysis
To verify the idea that feed-forward networks can better extract sequence features, the authors conducted feature representation analysis based on CKA (Centered Kernel Alignment) similarity. The lower the CKA similarity, the greater the feature differences between the model’s lower and upper layers.
It is noteworthy that previous research indicates that time series prediction, as a fine-grained feature learning task, often prefers higher CKA similarity.
The authors calculated the bottom-layer to top-layer CKA for both the inverted and non-inverted models, yielding results that confirm that the iTransformer has learned better sequence features, thereby achieving better prediction performance.
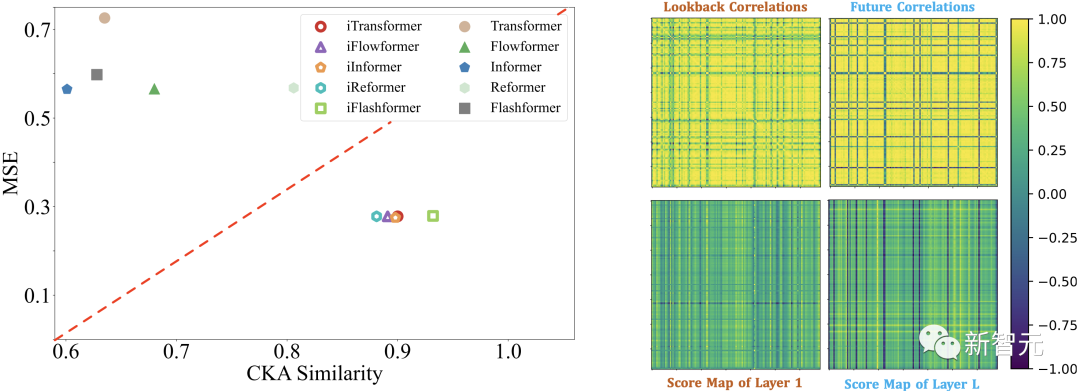
3. Variable Correlation Analysis
As shown in the figure above, the attention mechanism acting on the variable dimension exhibits stronger interpretability in the learned attention map. By visualizing examples from the Solar-Energy dataset, the following observations were made:
-
In the shallow attention module, the learned attention map is more similar to the variable correlations of historical sequences.
-
In the deep attention module, the learned attention map is more similar to the variable correlations of the sequences to be predicted.
This indicates that the attention module has learned more interpretable variable correlations and has encoded the temporal features of historical observations in the feed-forward network, progressively decoding them into the sequences to be predicted.
Conclusion
Inspired by the characteristics of multi-dimensional time series data, the authors reflect on the issues existing in the current Transformers for modeling time series data and propose a universal time series prediction framework called iTransformer.
The iTransformer framework innovatively introduces an inverted perspective to observe time series, allowing Transformer modules to perform their respective duties and effectively address the modeling challenges of the two dimensions of time series data, demonstrating excellent performance and generality.
In response to doubts about the effectiveness of Transformers in time series prediction, this discovery by the authors may inspire subsequent related research, bringing Transformers back to a mainstream position in time series prediction and providing new ideas for foundational model research in the time series data field.

