Machine learning is a branch of artificial intelligence dedicated to building systems that can learn and adapt automatically. It utilizes statistical models to visualize, analyze, and predict data. A general machine learning model consists of a dataset (for training the model) and an algorithm (to learn from the data). However, some models often have low accuracy, resulting in less accurate outcomes. One of the simplest solutions to overcome this issue is to use ensemble learning on machine learning models.
Ensemble learning is a meta-method that combines multiple machine learning models to create an optimized model, thereby improving model performance. Ensemble learning can easily reduce overfitting, preventing the model from performing well during training but failing to produce good results during testing.
In summary, ensemble learning has the following advantages:
-
Increases model performance
-
Reduces overfitting
-
Decreases variance
-
Provides higher predictive accuracy compared to individual models.
-
Can handle both linear and nonlinear data.
-
Ensemble techniques can be used to solve regression and classification problems.
Below we will introduce various methods of ensemble learning:
Voting
Voting is an ensemble learning method that combines predictions from multiple machine learning models to produce results. Multiple base models are trained on the entire dataset to make predictions. Each model’s prediction is considered a “vote.” The prediction with the majority of votes will be selected as the final prediction.
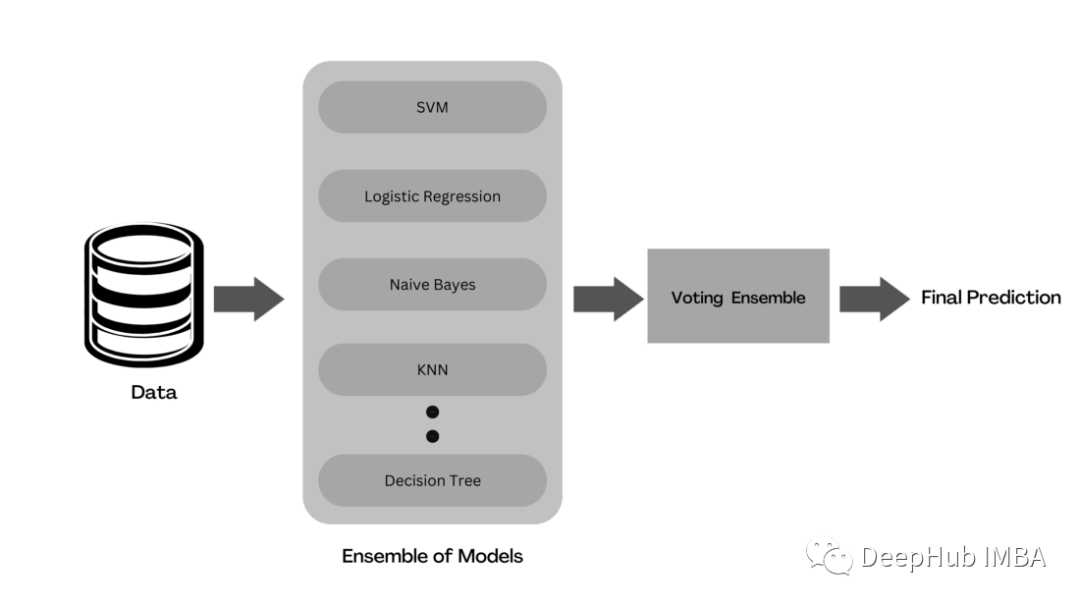
There are two types of voting used to aggregate base predictions – hard voting and soft voting.
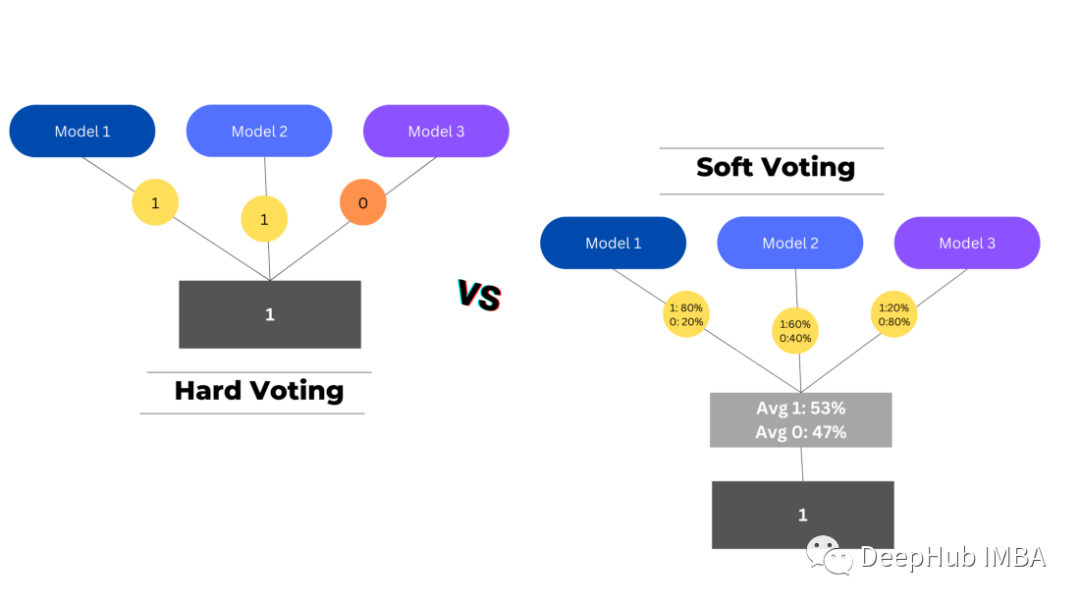
Hard voting selects the prediction with the highest number of votes as the final prediction, while soft voting combines the probabilities of each class in each model, selecting the class with the highest probability as the final prediction.
In regression problems, it works somewhat differently since we are not looking for the most frequent class but rather taking the predictions from each model and calculating their average to arrive at the final prediction.
from sklearn.ensemble import VotingClassifier
## Base Models
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
ensemble_voting = VotingClassifier(
estimators = [('dtc',DecisionTreeClassifier(random_state=42)),
('lr', LogisticRegression()),
('gnb', GaussianNB()),
('knn',KNeighborsClassifier()),
('svc',SVC())],
voting='hard')
ensemble_voting.fit(X_train,y_train)Bagging
Bagging combines several weak machine learning models and aggregates their predictions to produce the best prediction. It is based on bootstrap aggregation, where bootstrap is a sampling technique that draws random samples from a dataset using replacement. Aggregation refers to the process of combining several predictions to produce the final prediction.

Random Forest is one of the most famous and commonly used models that utilizes Bagging. It consists of a large number of decision trees that operate as a whole. It uses the concepts of Bagging and feature randomness to create each independent tree. Each decision tree is trained on samples randomly drawn from the data. In Random Forest, the trees we end up with are trained not only on different datasets but also use different features to predict outcomes.
Bagging typically has two types – an ensemble of decision trees (called Random Forest) and an ensemble of models other than decision trees. Both work similarly, using aggregation methods to generate final predictions, with the only difference being the models they are based on. In sklearn, we have a BaggingClassifier class to create models other than decision trees.
## Bagging Ensemble of Same Classifiers (Decision Trees)
from sklearn.ensemble import RandomForestClassifier
classifier= RandomForestClassifier(n_estimators= 10, criterion="entropy")
classifier.fit(x_train, y_train)
## Bagging Ensemble of Different Classifiers
from sklearn.ensemble import BaggingClassifier
from sklearn.svm import SVC
clf = BaggingClassifier(base_estimator=SVC(),
n_estimators=10, random_state=0)
clf.fit(X_train,y_train)Boosting
The boosting ensemble method transforms weak learners into strong learners by emphasizing the errors of previous models. Boosting implements homogeneous ML algorithms in a sequential manner, where each model attempts to improve the stability of the entire process by reducing the errors of the previous model.
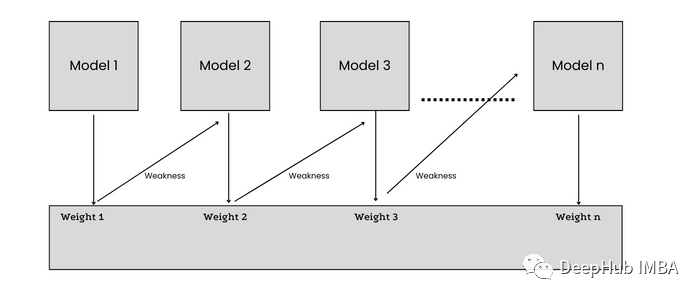
When training the n+1 model, each data point in the dataset is assigned equal weight, so samples misclassified by model n are given more weight (importance). Errors are passed from n learners to n+1 learners, where each learner attempts to reduce the error.
ADA Boost is one of the most basic models that uses Boosting to generate predictions. ADA Boost creates a forest of decision stumps (a stump is a decision tree with only one node and two leaves), unlike Random Forest which creates a forest of complete decision trees. It assigns higher weights to misclassified samples and continues training the model until a lower error rate is achieved.
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
dt = DecisionTreeClassifier(max_depth=2, random_state=0)
adc = AdaBoostClassifier(base_estimator=dt, n_estimators=7, learning_rate=0.1, random_state=0)
adc.fit(x_train, y_train)Stacking
Stacking is also known as stacked generalization, a form of ensemble technique proposed by David H. Wolpert in 1992, aimed at reducing errors by using different generalizers.
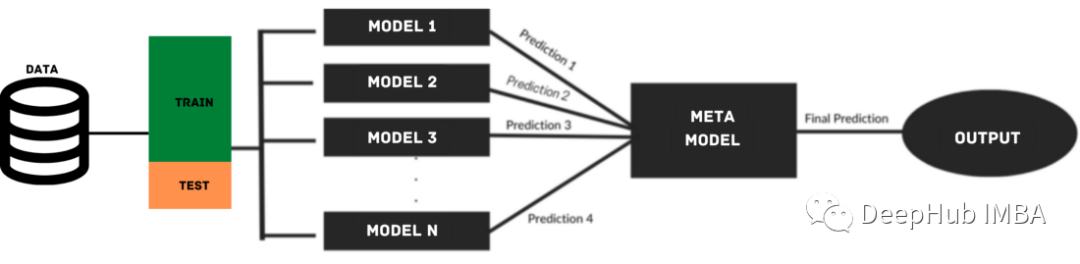
The stacking model utilizes predictions from multiple base models to build a meta-model for generating final predictions. The stacking model consists of multiple layers, where each layer contains several machine learning models whose predictions are used to train the next layer model.
During the stacking process, the data is divided into training and testing sets. The training set is further divided into k-folds. The base models are trained on k-1 parts and make predictions on the kᵗʰ part. This process is repeated until each fold is predicted. The base models are then fitted to the entire dataset, and performance is calculated. This process also applies to other base models.
Predictions from the training set are used as features to build the second layer or meta-model. This second-level model is used to predict the test set.
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import StackingClassifier
base_learners = [
('l1', KNeighborsClassifier()),
('l2', DecisionTreeClassifier()),
('l3',SVC(gamma=2, C=1)))
]
model = StackingClassifier(estimators=base_learners, final_estimator=LogisticRegression(),cv=5)
model.fit(X_train, y_train)Blending
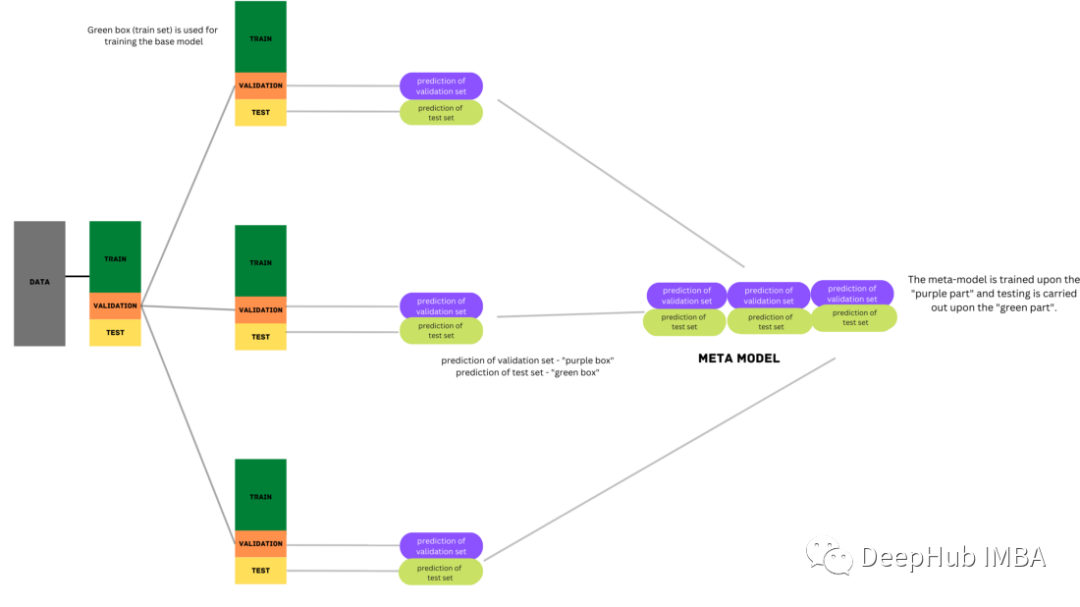
Blending is another form of ensemble learning technique derived from Stacking, with the key difference being that it uses a holdout (validation) set from a training set for predictions. Simply put, predictions are only made on the holdout dataset. The holdout dataset and predictions are used to construct the second-level model.
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
## Base Models
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
## Meta Learner
from sklearn.linear_model import LogisticRegression
## Creating Sample Data
X,y = make_classification(n_samples=10000, n_features=20, n_informative=15, n_redundant=5, random_state=42)
## Training a Individual Logistic Regression Model
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)
logrec = LogisticRegression()
logrec.fit(X_train,y_train)
pred = logrec.predict(X_test)
score = accuracy_score(y_test, pred)
print('Base Model Accuracy: %.3f' % (score*100))
## Defining Base Models
def base_models():
models = list()
models.append(('knn', KNeighborsClassifier()))
models.append(('dt', DecisionTreeClassifier()))
models.append(('svm', SVC(probability=True)))
return models
## Fitting Ensemble Blending Model
## Step 1:Splitting Data Into Train, Holdout(Validation) and Test Sets
X_train_full, X_test, y_train_full, y_test = train_test_split(X, y, test_size=0.3, random_state=1)
X_train, X_val, y_train, y_val = train_test_split(X_train_full, y_train_full, test_size=0.33, random_state=1)
## Step 2: train base models on train set and make predictions on validation set
models = base_models()
meta_X = list()
for name, model in models:
# training base models on train set
model.fit(X_train, y_train)
# predict on hold out set
yhat = model.predict_proba(X_val)
# storing predictions
meta_X.append(yhat)
# horizontal stacking predictions
meta_X = np.hstack(meta_X)
## Step 3: Creating Blending Meta Learner
blender = LogisticRegression()
## training on base model predictions
blender.fit(meta_X, y_val)
## Step 4: Making predictions using blending meta learner
meta_X = list()
for name, model in models:
yhat = model.predict_proba(X_test)
meta_X.append(yhat)
meta_X = np.hstack(meta_X)
y_pred = blender.predict(meta_X)
# Evaluate predictions
score = accuracy_score(y_test, y_pred)
print('Blending Accuracy: %.3f' % (score*100))
---------------------------------
Base Model Accuracy: 82.367
Blending Accuracy: 96.733Conclusion
After reading this article, you may wonder if there is a better method to choose a model or which ensemble technique to use if necessary?
In this case, we always recommend starting with a simple individual model and then testing it with different modeling techniques (like ensemble learning). In some cases, a single model may perform better than an ensemble model, sometimes significantly better.
It is important to note that ensemble learning should never be the first choice but rather the last option. The reason is simple: training an ensemble model will take a lot of time and require a lot of processing power.
Returning to our question, ensemble models are designed to improve the predictability of models by combining several base models of the same category. Each ensemble technique is the best in its own way and helps improve model performance.
If you are looking for a simple and easy-to-implement ensemble method, then you should use Voting. If your data has high variance, then you should try Bagging. If the base models trained have high bias in model predictions, you can try different Boosting techniques to improve accuracy. If multiple base models perform well on the data and you do not know which one to choose as the final model, then you can use Stacking or Blending methods. Of course, which method performs the best still depends on the data and feature distribution.
Finally, ensemble learning techniques are powerful tools for improving model accuracy and performance, as they easily reduce the chances of data overfitting and underfitting, especially when competing, this is key to improving scores.
Editor / Zhang Zhihong
Reviewer / Fan Ruiqiang
Re-examiner / Zhang Zhihong
Click below
Follow us
Read the original text
