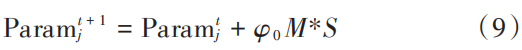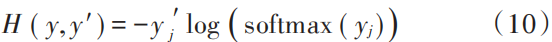Peng Cheng 1,2,Jiang Jinyuan 1,Li Fengjuan 1
(1.Hunan University of Technology, School of Computer Science, Zhuzhou, Hunan 412007; 2.Central South University, School of Automation, Changsha, Hunan 410083)
Abstract: This paper addresses the difficulty of hyperparameter configuration in fault diagnosis using deep learning methods. To effectively optimize the set of hyperparameters, we propose an optimization algorithm that combines normal distribution and Lévy flight (NLF). Based on this, we propose the NLF-LSTM method for rolling bearing fault diagnosis. By leveraging the concentration of normal distribution and the dispersion of Lévy flight, we sample the hyperparameter set multiple times and train it using Long Short-Term Memory (LSTM) networks to obtain the optimal hyperparameter set. We then build a fault diagnosis model using the optimal hyperparameter set to effectively diagnose three parts and ten states of rolling bearings. Experimental results show that compared with fault diagnosis methods based on SVM, the proposed method can significantly improve the ability to identify rolling bearing fault conditions. This also indicates that the NLF-LSTM fault diagnosis method not only reduces the difficulty of hyperparameter configuration for researchers but also makes the fault diagnosis method more end-to-end and intelligent.
Keywords: Rolling Bearing; Fault Diagnosis; Deep Learning; Long Short-Term Memory Neural Network; Hyperparameters; Normal Distribution; Lévy Flight; End-to-End
Classification Number: TN98-34 Document Identification Code: A
Article Number: 1004-373X(2022)01-0142-07
In practical engineering environments, mechanical equipment often operates under complex conditions such as high temperature, heavy load, and strong impact, making component aging and faults inevitable during operation. Failure to detect faults in a timely manner can lead to even greater losses, thus research on fault diagnosis methods is of significant practical importance. To date, many scholars both domestically and internationally have made substantial achievements in the effective diagnosis of mechanical faults, which can be broadly classified into two categories: traditional intelligent fault diagnosis methods[1] and deep learning-based diagnosis methods[2]. With the significant upgrade of data acquisition equipment, the volume of data has grown geometrically, providing substantial data support for deep learning methods[3]. Deep learning-based diagnosis methods have gradually outperformed traditional methods, leading researchers to increasingly utilize deep learning techniques to solve fault diagnosis problems. These techniques mainly include Stacked Auto Encoder (SAE), Deep Belief Network (DBN), Convolutional Neural Network (CNN), and Recurrent Neural Network (RNN)[4].
Literature[5] proposes a method for bearing fault diagnosis based on dynamic learning rate adjustment to accelerate the convergence of SAE. Literature[6] establishes the optimal SAE model using a firefly algorithm for bearing fault diagnosis. Literature[7] combines Adaptive Resonance Theory (ART) neural networks with DBN to construct the ART-DBN model to improve the poor diagnostic performance of DBN on small sample datasets. Literature[8] proposes a bearing fault diagnosis method based on a 2D CNN using time-frequency maps obtained through short-time Fourier transform preprocessing. Literature[9] uses particle swarm optimization to optimize seven key parameters of the CNN model and constructs a deep learning model to diagnose the fault status of rotating machinery. Currently, fault diagnosis based on RNN[10] often utilizes its variant, Long Short-Term Memory (LSTM), to achieve diagnosis[11]. Literature[12] extracts bearing fault features using wavelet packet transformation, and then uses LSTM to diagnose three fault states of wind turbine rolling bearings. Literature[13] combines Deep Wavelet Convolutional Auto-encoder (DWCAE) and LSTM for diagnosing three fault states of bearings.
Literature[14] constructs a diagnostic model using LSTM, named e2e-LSTM, and proposes end-to-end fault diagnosis for the first time. Numerous studies indicate that deep learning methods perform well in feature extraction and learning tasks, and the fault recognition effectiveness of deep learning-based fault diagnosis methods is significantly better than that of traditional machine learning methods. Therefore, many researchers have proposed a variety of fault diagnosis methods based on the application and improvement of deep learning techniques. Meanwhile, with the introduction of deep learning, fault diagnosis is gradually shifting from raw data to diagnostic results in an end-to-end manner, and the number of model hyperparameters is increasing. Solving the hyperparameter setting problem through algorithms will become the most important approach.
Since the proposal of end-to-end fault diagnosis methods based on deep learning, the limitations of manual parameter tuning have become increasingly prominent. For example, the e2e-LSTM fault diagnosis method proposed in Literature[14] requires repeated deliberation on the values of the LSTM model’s hyperparameters, which is a process that consumes a lot of effort. Thus, algorithmically optimizing hyperparameters will break this dilemma. Common hyperparameter tuning algorithms include grid search[15], random search[16], Bayesian optimization[17], and swarm intelligence optimization algorithms[18-19]. These optimization algorithms can solve the hyperparameter setting problem of deep learning models to a certain extent, but they also have limitations: grid search is simple to implement, but its optimization efficiency decreases geometrically with an increase in the number of hyperparameters; random search can achieve optimization objectives faster than grid search, but still requires multiple iterations; Bayesian optimization requires a substantial amount of expertise and prior data support; and intelligent optimization algorithms heuristically search for the optimal hyperparameter combination, which are currently more commonly used optimization algorithms, but practical implementation still faces issues, such as the complexity of operations like encoding and crossover in genetic algorithms (GA) and the tendency of particle swarm optimization (PSO) to get trapped in local optima. In summary, hyperparameter optimization algorithms still have many shortcomings. To address the issue of excessive iterations and slow convergence of random search, Literature[20] proposes an improved random search algorithm that focuses on local extrema with a probabilistic sampling approach to complete hyperparameter optimization, and introduces the RS-LSTM fault diagnosis method. This algorithm significantly speeds up the search process, and the RS-LSTM fault diagnosis method also achieves high recognition accuracy, although the involvement of local extrema somewhat sacrifices randomness, increasing the possibility of getting trapped in local optima.
To effectively resolve the hyperparameter configuration issue of deep learning models, this paper proposes the Normal Distribution and Lévy Flight (NLF) search algorithm to complete hyperparameter optimization, and introduces a bearing fault diagnosis method based on NLF-LSTM. The main contributions of this work are as follows:
1) An optimization algorithm is proposed for hyperparameter optimization. The proposed algorithm is easy to implement and incorporates the advantages of animal behavior simulation in swarm intelligence algorithms to escape local extrema, effectively achieving the goal of hyperparameter optimization.
2) In practical engineering applications, a new fault diagnosis method is proposed, making fault diagnosis more intelligent.
1 Basic Theory
1.1 LSTM Network
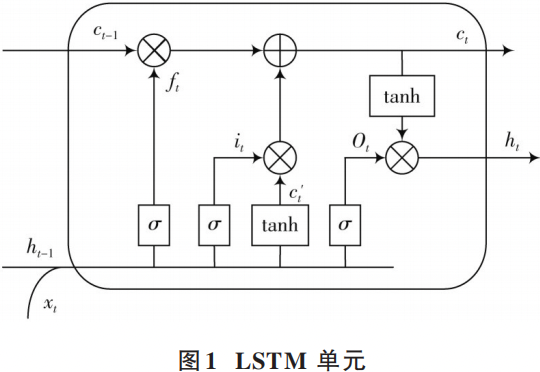
In deep learning technology, RNN is a classic supervised deep learning model widely used in various fields such as natural language processing and speech recognition. Since sensor-collected data can essentially be regarded as time-series data, it also has good application prospects in fault diagnosis. However, the problems of exploding and vanishing gradients during backpropagation greatly affect the training performance of RNNs. LSTM effectively addresses these issues through a three-gate structure (input gate i, forget gate f, output gate o). The LSTM unit includes a three-gate structure and a memory cell c (t to store long-term memory), as shown in Figure 1.
The calculations involved in the forward propagation algorithm of LSTM include:
In the equation:Wf,Wi,Wo,Wc are the weight matrices for the forget gate, input gate, output gate, and memory cell, respectively; bf,bi,bo ,bc are the bias matrices for the forget gate, etc.; ht-1,ct-1 are the output and memory cell of the LSTM unit at time t-1; xt is the input at the current time.
1.2 Normal Distribution and Lévy Flight
Normal distribution is a common probability distribution. If a random variable follows a normal distribution N(μ,σ2), the range of values for the random variable in practice can be determined using the 3σ rule, which indicates that the values lie within (μ-3σ,μ+3σ). The probability of the random variable being near μ is the highest, which is similar to the local development that search algorithms aim to achieve. Therefore, normal distribution is introduced into random search. By making the hyperparameter values follow N(best_params,c), the hyperparameters are concentrated around local extrema, thereby exploring better hyperparameter sets. For discrete hyperparameters such as the number of network layers, rounding is necessary; that is, the probability of discrete hyperparameter taking value a is given by P(a)=P(a-0.5<X<a+0.5). According to the 3σ rule, the value range for updating hyperparameters is determined by the mean and variance, and this range remains constant, which may slow down the search process. To further strengthen the local development capability, we propose a dynamically changing variance that gradually decreases non-linearly with the number of iterations, as shown in equation (7):
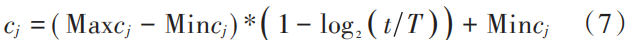 In the equation:Maxcj is the maximum value of variance j; Mincj is the minimum value of variance j; t is the current iteration number; T is the total number of iterations.
Lévy distribution (Lévy Distribution) is a probability distribution proposed by French mathematician Lévy (Paul Pierre Lévy) in the 1930s. It is well known that the foraging trajectories of most animals in nature follow Lévy distribution, which helps animals survive more effectively. Common methods for implementing Lévy distribution are proposed in Literature[21], as shown in equation (8):
In the equation:u and v follow normal distributions N(0,σ2u) and N(0,σ2v), and
In the equation:Maxcj is the maximum value of variance j; Mincj is the minimum value of variance j; t is the current iteration number; T is the total number of iterations.
Lévy distribution (Lévy Distribution) is a probability distribution proposed by French mathematician Lévy (Paul Pierre Lévy) in the 1930s. It is well known that the foraging trajectories of most animals in nature follow Lévy distribution, which helps animals survive more effectively. Common methods for implementing Lévy distribution are proposed in Literature[21], as shown in equation (8):
In the equation:u and v follow normal distributions N(0,σ2u) and N(0,σ2v), and  , Γ is the standard gamma function, and σv= 1.
As a Lévy flight that follows Lévy distribution, it performs random walks with dynamically changing step lengths, effectively avoiding getting stuck in the current position and participating in search algorithms, thereby improving the global search capability of the algorithms[22]. Therefore, using Lévy flight to update the values of hyperparameters can avoid the deficiencies in global exploration caused by normal distribution sampling, and the hyperparameter update formula is as follows:
In the equation:t is the current iteration number; φ0=rand (0, 1);M=Paramj-bestj;S~L(α).
, Γ is the standard gamma function, and σv= 1.
As a Lévy flight that follows Lévy distribution, it performs random walks with dynamically changing step lengths, effectively avoiding getting stuck in the current position and participating in search algorithms, thereby improving the global search capability of the algorithms[22]. Therefore, using Lévy flight to update the values of hyperparameters can avoid the deficiencies in global exploration caused by normal distribution sampling, and the hyperparameter update formula is as follows:
In the equation:t is the current iteration number; φ0=rand (0, 1);M=Paramj-bestj;S~L(α).
2 Rolling Bearing Fault Diagnosis Based on NLF-LSTM
The ultimate goal of rolling bearing fault diagnosis is to extract the bearing status from the data. The previous overall process included three steps: data preprocessing, feature extraction, and fault status diagnosis. With the introduction of deep learning, researchers have proposed end-to-end fault diagnosis methods for bearings. Compared with traditional machine learning methods, this approach does not require feature extraction, but the importance of setting hyperparameters has become increasingly prominent. A suitable combination of hyperparameters can effectively enhance the fault diagnosis capability. Therefore, the current process of end-to-end fault diagnosis based on deep learning includes: data preprocessing, hyperparameter setting, and fault status diagnosis.
2.2 Hyperparameter Optimization
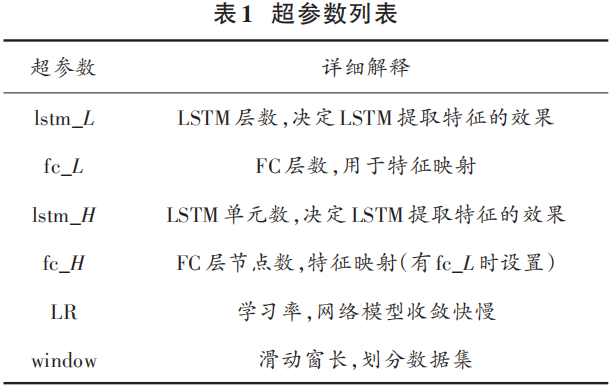
Optimization problems have corresponding objective functions; in this case, the fault diagnosis problem’s objective function is the maximum recognition accuracy of fault categories:max(PD), where P is the number of correctly classified samples, and D is the total number of samples in the test set. The hyperparameters that need to be set for the fault diagnosis model are shown in Table 1.
To obtain more experimental data to meet the needs of deep learning, overlapping sampling techniques using sliding windows are often employed to expand the dataset. Therefore, the sliding window length is optimized algorithmically to find a more suitable time-domain sample length. The partitioning method is shown in Figure 2. In this paper, the default setting is that the sliding length between samples equals the sliding window length (also known as time-domain sample length)/2.
2.3 Fault Diagnosis
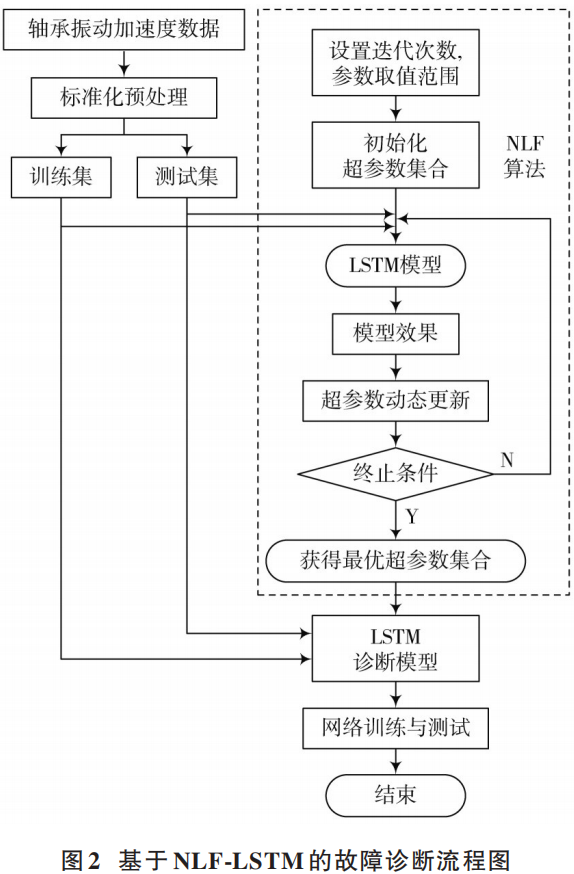
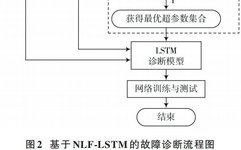
This paper uses the NLF algorithm to simplify the hyperparameter setting process, and the final established NLF-LSTM rolling bearing fault diagnosis model is more intelligent. The specific process is shown in Figure 2.
From the flowchart, the main steps of the NLF-LSTM based rolling bearing fault diagnosis method are as follows:
1) Obtain vibration acceleration data of rolling bearings and perform standardization processing.
2) Use the NLF algorithm described in Section 2.1 to optimize the deep learning model structure, learning rate, and time-domain sample length. In this case, the deep learning model adopts a combination of multi-layer LSTM units and a multi-layer fully connected layer to construct fault diagnosis feature extraction and mapping, plus a softmax layer to obtain class probabilities.
3) Model training and testing. Use the structured hyperparameters to construct the LSTM model, obtain dataset samples using the sliding window length, and partition the training and testing sets according to an 80:20 ratio. Supervised training is conducted using the learning rate obtained in step 2), where the training process includes inputting data according to batch size, calculating cross-entropy, backpropagating, and updating network weights. After training, the testing set is used to verify the training results. The fault diagnosis method based on NLF-LSTM implemented through the above steps can detect the specific wear locations and severity of rolling bearings.
3 Experiments and Results Analysis
3.1 Experimental Data Source
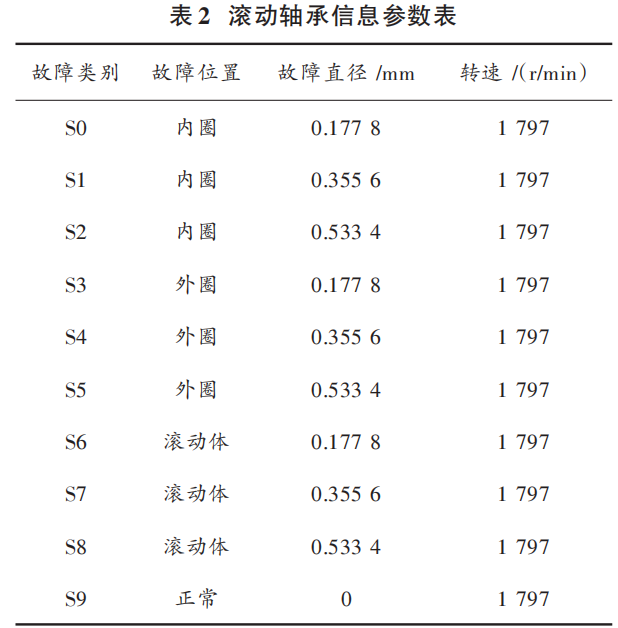
The data is sourced from the rolling bearing dataset (CWRU) from Case Western Reserve University, based on the data of bearing model 6205-2RS JEMSKF deep groove ball bearing with a sampling frequency of 12 kHz. The experimental diagnostic labels contain data for 10 states, namely S0~S9, with vibration signal information shown in Table 2.
3.2 Experimental Environment and Model Evaluation Standards
This paper uses Pytorch to train the mixed neural network model constructed with hyperparameters. Pytorch is a deep learning framework that is second only to TensorFlow in popularity. It was released by the Facebook AI Research team in 2017, specifically designed for GPU-accelerated deep learning programming. The experiments are conducted in an environment built on Windows 10 with Pytorch 1.5.0 and CUDA 10.2. The optimization algorithm for network training adopts the Adam gradient optimizer in Pytorch[23].
The fault diagnosis problem is generally a multi-class single-label problem, so the cross-entropy loss value is used as the loss function during network training, and it is used to update the internal weights of the network. In Pytorch, the loss value is calculated using nn.CrossEntropyLoss( ). Unlike other formulas for calculating cross-entropy, nn.CrossEntropyLoss includes a softmax process, defined as follows:
In the equation, y and y′ are the output of the neural network and the classification label, respectively.
3.3 Hyperparameter Optimization
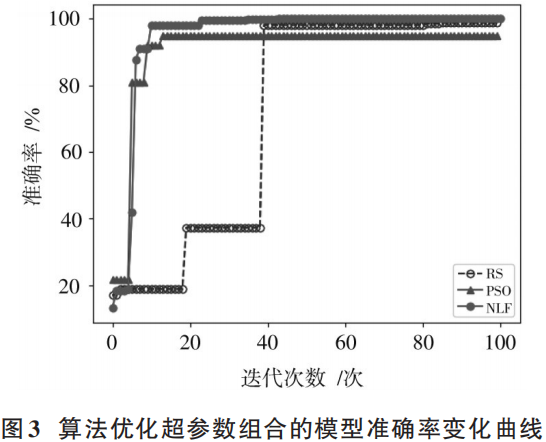
Using the NLF algorithm from Section 2.2, we obtain the hyperparameter set to construct the NLF-LSTM model. To demonstrate the superiority of the NLF algorithm, we compare it with the RS algorithm[20] and the PSO algorithm[18], obtaining the accuracy variation curves of hyperparameter tuning, as shown in Figure 3.
From Figure 3, it can be seen that after a certain degree of iterative optimization, all three algorithms can achieve high accuracy. However, RS requires a larger number of iterations; in contrast, the NLF algorithm reduces the number of iterations by about 75%, indicating that the NLF algorithm can effectively and efficiently complete hyperparameter optimization for deep models. In terms of the accuracy achieved after final convergence, the NLF algorithm is the best among the three algorithms, suggesting that it can avoid situations similar to PSO getting trapped in local optima to a certain extent.
Overall, the NLF algorithm can effectively solve the hyperparameter tuning problem, exploring a more comprehensive hyperparameter space compared to the other two algorithms, and the optimized hyperparameter combinations are more suitable.
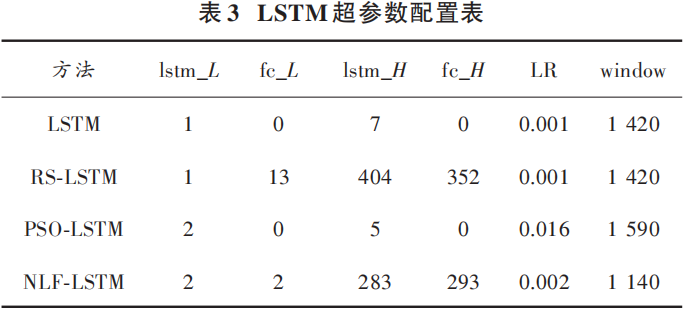
Through the NLF algorithm, the optimal hyperparameter combination obtained is {lstm_L:2, fc_L:2, lstm_H:283, fc_H:293, LR:0.002, window:1140}.
3.4 NLF-LSTM Fault Diagnosis Result Analysis
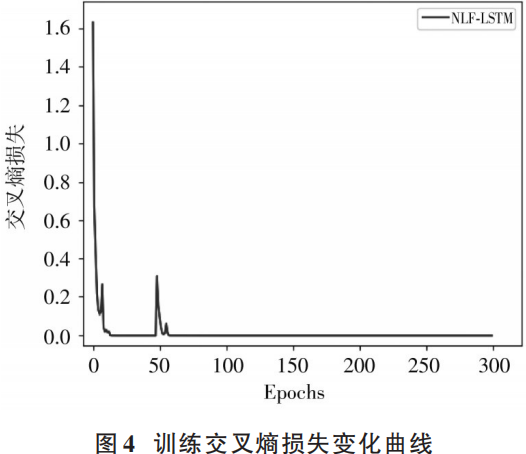
Using the sliding window technique to expand the CWRU dataset, we then partition the dataset into training and testing sets; based on lstm_L, lstm_H, fc_L, fc_H, we construct the LSTM diagnostic model. By training the LSTM model using the training set and the learning rate obtained from LR, we can observe the changes in cross-entropy loss during the training process, as shown in Figure 4.
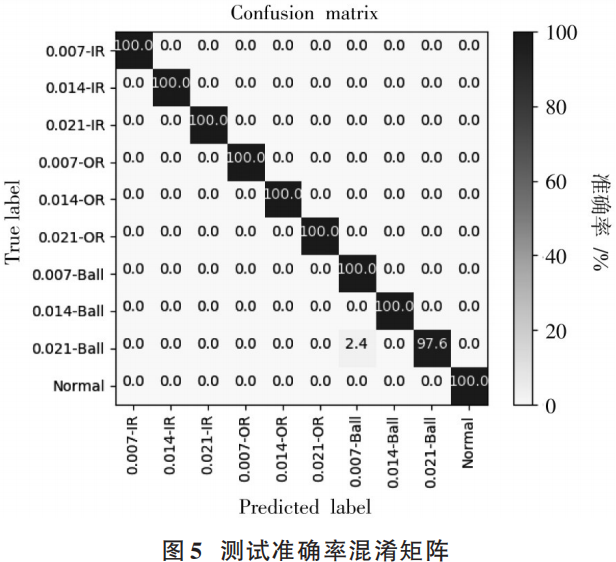
From Figure 4, it can be seen that as the number of training iterations increases, the cross-entropy loss gradually decreases, ultimately approaching 0, indicating that the NLF-LSTM model training can effectively converge. We then use the testing set to validate the diagnostic results, taking the average accuracy of the last 10 epochs, resulting in an accuracy of 99.89%, with the confusion matrix shown in Figure 5 (labels X-IR, X-OR, X-Ball, Normal represent inner ring fault, outer ring fault, rolling element fault, and normal, respectively; X indicates fault severity).
To validate the effectiveness of NLF-LSTM for fault diagnosis, we compare it with shallow LSTM, LSTM optimized by RS algorithm (RS-LSTM), and LSTM optimized by PSO algorithm (PSO-LSTM), with the hyperparameter configurations for the LSTM model shown in Table 3.
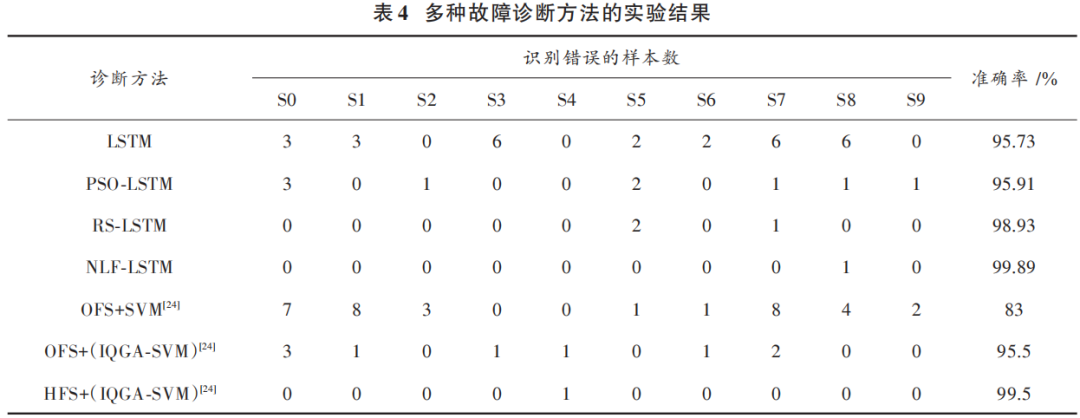
Simultaneously, we reference the experimental results from Literature [24] for comparison. Literature [24] is based on the same dataset, also focusing on the classification recognition of 10 bearing states. The comparative results of various fault diagnosis methods are shown in Table 4.
From Table 4, it can be seen that for methods based on LSTM, those not using algorithmic optimization have a higher number of misclassifications. After hyperparameter optimization, the accuracy reached 95.91%, 98.93%, and 99.89%, respectively, demonstrating varying degrees of improvement, with NLF-LSTM achieving the best performance, increasing by 4.35%. For methods based on SVM, the fault recognition rate of the SVM model optimized by IQGA has also improved significantly, highlighting the critical importance of hyperparameter optimization in fault diagnosis methods.
Comparing the seven fault diagnosis methods in the table, it can be seen that the diagnostic capability of the LSTM model generally surpasses that of SVM-based models, primarily due to the excellent feature extraction capability of the LSTM model, making fault diagnosis both easier to implement and more effective.
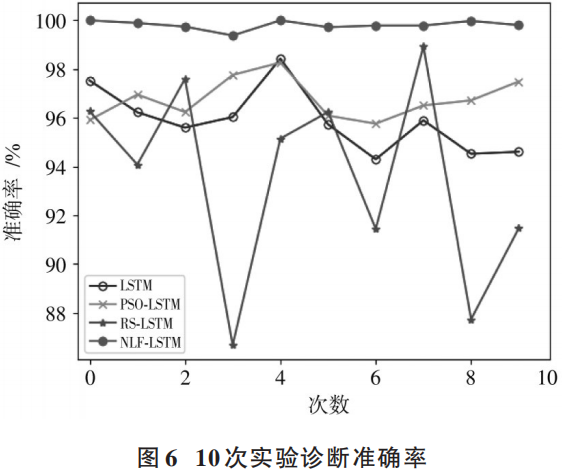
To further verify the stability of the NLF-LSTM diagnostic capability, we conduct repeated experiments with four models: LSTM, PSO-LSTM, RS-LSTM, and NLF-LSTM, with the results shown in Figure 6.
In terms of stability, Figure 6 shows that the diagnostic results of RS-LSTM exhibit the greatest volatility during repeated experiments, primarily due to the instability of random search results leading to excessive FC layer counts in the LSTM model, resulting in significant deviations in training outcomes, sometimes even lower than those of a simple LSTM model. In contrast, PSO-LSTM performs relatively better, while the proposed NLF-LSTM diagnostic method is the most stable. In summary, the proposed NLF algorithm can optimize the hyperparameters of the LSTM network, and the constructed NLF-LSTM diagnostic method achieves very high accuracy.
The concept of end-to-end originally described the relationship between devices at both ends of network transmission, while the end-to-end fault diagnosis method based on LSTM achieves direct diagnosis from raw collected data to fault type identification through deep learning models, effectively addressing issues such as difficulty in feature extraction and selection. This method is a primary solution for intelligent fault diagnosis, but hyperparameter settings still require human intervention, significantly reducing the degree of intelligence in fault diagnosis. This paper proposes the NLF algorithm to attempt to resolve the hyperparameter setting issue. Experimental results show that the NLF algorithm significantly reduces the number of iterations in the optimization process, demonstrating the feasibility of the proposed algorithm. The NLF-LSTM model constructed with the optimized hyperparameter combination achieves higher fault diagnosis accuracy and more stable diagnostic results compared to various fault diagnosis methods based on SVM, fully indicating that the proposed NLF-LSTM diagnostic method is an effective new approach for rolling bearing fault diagnosis.
[1] Su Naiquan, Xiong Jianbin, Zhang Qinghua, et al. Overview of Research Methods for Rotating Machinery Fault Diagnosis [J]. Machine Tool and Hydraulic, 2018, 46(7): 133-139.
[2] Shen Tao, Li Shunming, Xin Yu. Overview of Research on Rotating Machinery Fault Diagnosis Based on Deep Learning [J]. Computer Measurement and Control, 2020, 28(9): 1-8.
[3] LECUN Y, BENGIO Y, HINTON G. Deep learning [J]. Nature, 2015, 521(7553): 436-444.
[4] Wen Chenglin, Lv Feiya. Overview of Fault Diagnosis Methods Based on Deep Learning [J]. Journal of Electronics and Information, 2020, 42(1): 234-248.
[5] Tang Wei, Zheng Yuan, Pan Hong, et al. Research on SAE Bearing Fault Diagnosis with Dynamic Learning Rate Adjustment [J]. Computer Engineering and Applications, 2020, 56(20): 264-269.
[6] Du Canyi, Lin Zusheng, Zhang Shaohui. Parameter Optimization SAE Method and Its Application in Bearing Fault Diagnosis [J]. Control Engineering, 2019, 26(5): 957-964.
[7] Chen Zizhao, Jiao Wencheng, Sun Huixian, et al. Fault Diagnosis Method Based on Improved Deep Belief Network [J]. Journal of Detection and Control, 2020, 42(4): 98-105.
[8] Zhang LZ, Xu WX, Jing LY, et al. Fault Diagnosis of Rotating Machinery Based on 2D Deep Convolutional Network [J]. Mechanical Strength, 2020, 42(5): 1039-1044.
[9] Li Tao, Duan Lixiang, Zhang Dongning, et al. Application of Adaptive Convolutional Neural Network in Rotating Machinery Fault Diagnosis [J]. Vibration and Shock, 2020, 39(16): 275-282.
[10] JOZEFOWICZ R, ZAREMBA W, SUTSKEVER I. An empirical exploration of recurrent network architectures [C]// Proceedings of the 32th International Conference on Machine Learning. Lille, France: JMLR, 2015: 2342-2350.
[11] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural computation, 1997, 9(8): 1735-1780.
[12] Zhang Jianfu, Song Yu, Li Gang, et al. Fault Diagnosis Method for Wind Turbine Rolling Bearings Based on Long Short-Term Memory Neural Network [J]. Computer Measurement and Control, 2017, 25(1): 16-19.
[13] Du Xiaolei, Chen Zhigang, Xu Xu, et al. Research on Bearing Fault Diagnosis Based on Wavelet Convolutional Auto-encoder and LSTM Network [J]. Electromechanical Engineering, 2019, 36(7): 663-668.
[14] Zhuang Yuxuan, Li Qi, Yang Bingru, et al. End-to-End Fault Diagnosis Method for Bearings Based on LSTM [J]. Noise and Vibration Control, 2019, 39(6): 187-193.
[15] Zhang Gongrang, Wan Fei. Application of Grid Search SVM in Intrusion Detection [J]. Computer Technology and Development, 2016, 26(1): 97-100.
[16] BERGSTRA J, BENGIO Y. Random search for hyperparameter optimization [J]. Journal of machine learning research, 2012, 13(1): 281-305.
[17] BROCHU E, CORA V M, DE FREITAS N. A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning [EB / OL]. [2015-12-17]. https://www.doc88.com/p-6921575933489.html.
[18] Liu Kezhen, Gou Jiaqi, Luo Zhao, et al. Transformer Oil Dissolved Gas Concentration Prediction Method Based on Particle Swarm Optimization-LSTM Model [J]. Power Grid Technology, 2020, 44(7): 2778-2785.
[19] Zhu Huilong, Liu Xiaoyan, Liu Yao. Research on Neural Network Hyperparameter Optimization Based on Crowds [J]. Information Technology, 2018(11): 97-102.
[20] Chen Wei, Chen Jinxiong, Jiang Yongquan, et al. Rolling Bearing Fault Recognition Based on RS-LSTM [J]. China Science and Technology Papers, 2018, 13(10): 1134-1141.
[21] Mantegna R N. Fast, accurate algorithm for numerical simulation of Lévy stable stochastic processes [J]. Physical review, 1994, 49(5): 4677.
[22] Yang X S, Deb S. Cuckoo search via Lévy flights [C]// 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC). Coimbatore, India: IEEE, 2009: 210-214.
[23] KINGMA D, BA J. Adam: a method for stochastic optimization [EB / OL]. [2017-01-30]. http://arxiv.org/abs/1412.6980v8.
[24] Xu Di, Ge Jianghua, Wang Yaping, et al. Quantum Genetic Algorithm Optimized SVM for Rolling Bearing Fault Diagnosis [J]. Vibration, Testing and Diagnosis, 2018, 38(4): 843-851.
Author Introduction:
Peng Cheng (1982—), Male, from Changsha, Hunan, PhD, Associate Professor, research direction is intelligent information processing.
Jiang Jinyuan (1995—), Male, from Suining, Sichuan, Master’s student, research direction is industrial big data analysis.
Li Fengjuan (1995—), Female, from Yangquan, Shanxi, Master’s student, research direction is industrial big data analysis.
-End-
Click the link below to view historical articles
Good papers are “revised”!
CNKI’s continuous price increase is suspected of monopoly. How should academia and business balance?
The directory of Modern Electronic Technology 2019 Issue 12
Which universities published the most SCI papers and granted patents in 2017?
Modern Electronic Technology selected in Overview of Chinese Core Journals
Academician of the Chinese Academy of Sciences: The paper-led by SCI has stifled scientific creativity
How to write a ‘Nature’ article overnight, listen to what the academicians say!
👇Scan the code to join the “Modern Electronic Technology Fan Group”
Come scan the code to join the group~
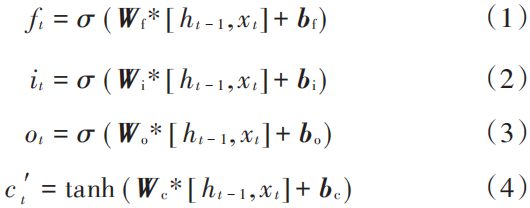
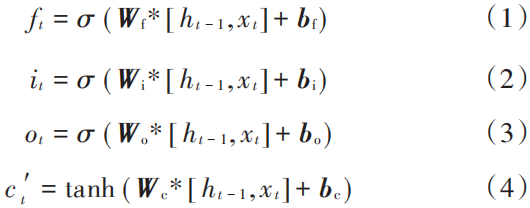
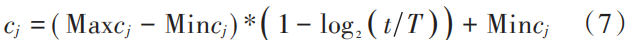

 , Γ is the standard gamma function, and σv= 1.
, Γ is the standard gamma function, and σv= 1.