|Author: Jiang Wenjie1 Deng Dongling1,2,†
(1 Tsinghua University Institute for Interdisciplinary Information Sciences)
(2 Shanghai Qi-Zhi Institute)
This article is selected from “Physics” 2021 Issue 2
Abstract Neural network quantum states are quantum states represented by artificial neural networks. Thanks to the breakthroughs in machine learning, especially deep learning in recent years, the study of neural network quantum states has gained widespread attention and become a current hot frontier direction. This article will introduce different neural network quantum states, their physical properties and typical application scenarios, the latest progress, and the challenges faced.
Keywords Artificial Neural Networks, Quantum Many-Body Problems, Quantum Entanglement, Bell Inequalities
Artificial intelligence mainly has three development routes: symbolism, connectionism, and behaviorism[1]. Artificial neural networks are the cornerstone of connectionism and one of the key elements that have led to breakthroughs in deep learning in recent years. It was proposed based on the information processing patterns in biological brains, tracing back to the neuron model proposed by psychologist W. S. McCulloch and mathematician W. Pitts in 1943[2]. Currently, AI technology based on neural networks is bringing revolutionary changes to all aspects of human civilization[3]: from speech and image recognition to gravitational wave and black hole detection, as well as data mining, autonomous driving, medical diagnosis, and securities market analysis, etc. In 2018, the highest award in computer science—the Turing Award was awarded to three AI scientists Yoshua Bengio, Geoffrey Hinton, and Yann LeCun for their outstanding contributions in this field[4].
On the other hand, quantum mechanics is one of the most important foundational theories of modern physics[5]. Its importance is widely reflected in our daily lives and scientific explorations: from the semiconductor industry represented by electronic computers to novel superconducting phenomena, from ubiquitous chemical batteries to the mysterious black holes in the universe, the laws of change of all things are closely related to quantum mechanics.
However, studying quantum systems, especially quantum many-body systems, is very challenging. In practical research, there are very few problems that can be solved analytically, and for the vast majority of cases, we can only rely on numerical methods. For the most general cases, numerical methods require exponential amounts of computational resources, which is feasible for smaller physical systems, but becomes difficult to satisfy under classical computing systems as the system size increases[6]. The 1998 Nobel Prize in Chemistry winner Walter Kohn described this issue as the “exponential wall” difficulty[7]. To this end, physicists have made extensive efforts to develop a series of computational methods, with the famous Monte Carlo algorithm and renormalization group algorithm being typical representatives. However, these methods are not universal and each has its own applicable conditions. For example, the Monte Carlo algorithm can encounter sign problems when applied to certain frustrated systems, resulting in the algorithm requiring exponential time; while density matrix renormalization group algorithms are generally only suitable for one-dimensional low-entanglement entropy systems.
In the field of artificial intelligence, a similar problem is the curse of dimensionality. The curse of dimensionality was first proposed by dynamic programming pioneer and renowned applied mathematician Richard E. Bellman, describing the impact of the drastically different properties of high-dimensional versus low-dimensional datasets on computational problems[8]: as the data dimension increases, the distribution of finite-sized data in space becomes increasingly sparse, losing statistical significance. This requires that, under general circumstances, we need a very large data scale to obtain the statistical features of the dataset, which can impose a severe burden on computational resources. After years of development, many methods and tools have been proposed in the field of artificial intelligence to deal with high-dimensional problems. Artificial neural networks are a widely used example that can alleviate the difficulties posed by the curse of dimensionality to some extent. Simply put, artificial neural networks can be considered as universal function approximators. By adjusting network parameters, they can be used to approximate any smooth function[9].
Due to the similarity between the exponential wall difficulty and the curse of dimensionality, a natural idea is that neural networks can be used to tackle complex quantum problems. For instance, neural networks can be used to identify different quantum states and study their phase transitions (see the special article by Cai Zi in “Physics” 2017 Issue 9). On the other hand, we can also use neural networks to represent quantum states, with the main idea being to treat the neural network as a variational wave function, adjusting the network parameters to approximate the target wave function (such as the ground state of a many-body system), thereby solving the physical problems of interest. Traditional quantum many-body variational wave function methods require physicists to design specific variational functions for the problems being solved, while the neural network quantum state method can use relatively universal structures, relying less on prior knowledge. In addition, some optimization methods developed in the field of artificial intelligence can also be applied to neural network quantum states to improve algorithm efficiency.
In recent years, the method of solving quantum many-body problems through neural network quantum states has received widespread attention[10—12]. Currently, this is a very active frontier research direction. This article will introduce the physical properties and typical application scenarios of different neural network quantum states, as well as the latest developments in this direction. The neural networks involved include restricted Boltzmann machines, deep Boltzmann machines, feedforward neural networks, and recurrent neural networks, among others. Typical applications include: solving the ground state and dynamic evolution of quantum many-body systems, detecting quantum nonlocality, quantum tomography, and calculating out-of-time ordered correlators, etc. It is hoped that through this discussion, readers will appreciate the charm of neural network quantum states. As is well known, the neural network-based intelligent programs AlphaGo[13] and AlphaFold[14] have achieved milestone breakthroughs in Go and protein structure prediction, respectively. We hope that neural network quantum states can extend these breakthroughs to solving complex quantum many-body problems.
In quantum mechanics, all possible states of a closed physical system that does not interact with the outside world compose a Hilbert space, and each specific physical state is described by a vector in that space. The Hilbert space is mathematically a linear space, so once its basis vectors are determined, each physical state corresponding to a vector can be represented as a linear combination of the selected basis vectors. In practical physical problems, we often need to deal with situations that involve multiple subsystems, where the dimension of the system’s Hilbert space is the product of the dimensions of the corresponding spaces of each subsystem[15]. For example, suppose we need to describe a quantum system consisting of N spin particles, where each particle’s spin can take two possible values (up or down), corresponding to a Hilbert space dimension of 2, then the total spin state of the entire system has 2N possibilities, leading to a total Hilbert space dimension of 2N. Thus, representing the wave function in the most general case requires exponential amounts of computational resources, which poses a significant challenge for numerically solving quantum many-body problems.
Fortunately, the physical states of interest are generally subject to certain constraints, such as symmetry constraints or constraints of certain physical observables; each subsystem is not completely independent, and the states of subsystems influence each other, so the possible states of the overall system occupy only a small portion of the Hilbert space. In principle, for different physical systems, it is possible to use representation methods with specific structures to represent these physical states with relatively less computational resources[5]. The well-known tensor network is a typical example[16]. In physics, entanglement entropy is generally used to characterize the strength of correlations between quantum systems. Tensor networks can effectively represent physical states where entanglement entropy satisfies the area law (i.e., entanglement entropy is proportional to the surface area of the subsystem)[17]. Here, “effective” means that only polynomial orders of computational resources are needed. Another example is the neural network quantum states, which will be the focus of this article.
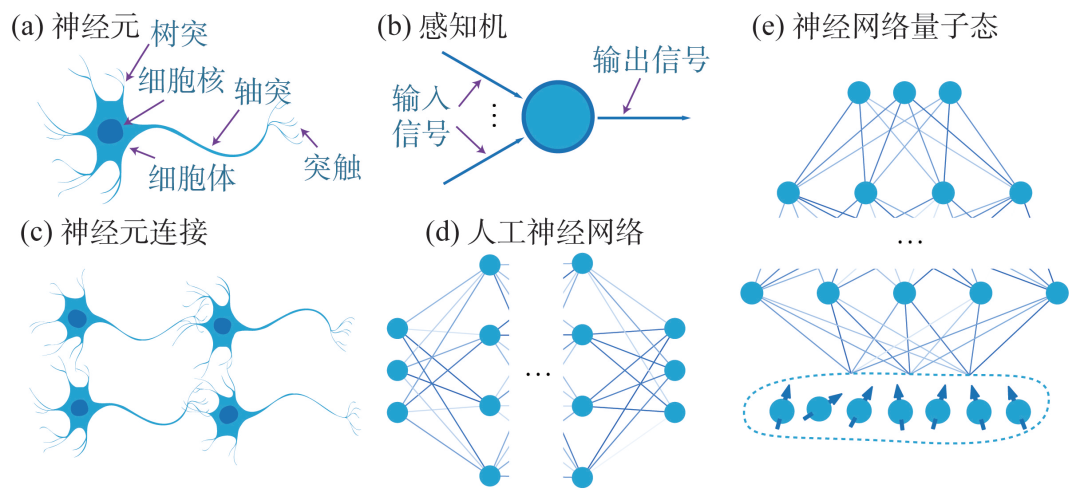
Figure 1 Neural Network Quantum State Diagram (a) Neurons in Biological Brain; (b) Perceptron; (c) Biological Neural Network; (d) Artificial Neural Network; (e) Neural Network Representation of Quantum States
Neural networks consist of numerous nodes (neurons) and the connections between them, as shown in Figure 1. Each node contains a specific output function known as an activation function. The connection between any two nodes represents the weighted value of the signal passing through that connection, known as the weight. Neural networks simulate the human brain in a simplified manner. The network’s output depends on its structure, connection patterns, weights, and activation functions. Neurons in a neural network are usually arranged in layers, with the first layer referred to as the input layer where data is fed in. The last layer is called the output layer, and the intermediate layers are referred to as hidden layers. If a neural network has more than two layers, it is typically called a deep neural network, and the machine learning models built on this basis are referred to as deep learning. Depending on the specific network structure and the direction of information propagation, neural networks can be classified into many types. Common neural networks include feedforward neural networks, convolutional neural networks, Boltzmann machines, recurrent neural networks, etc. Essentially, a quantum wave function is a function, and a neural network is a universal function approximator. Therefore, we can use neural networks to represent quantum states.
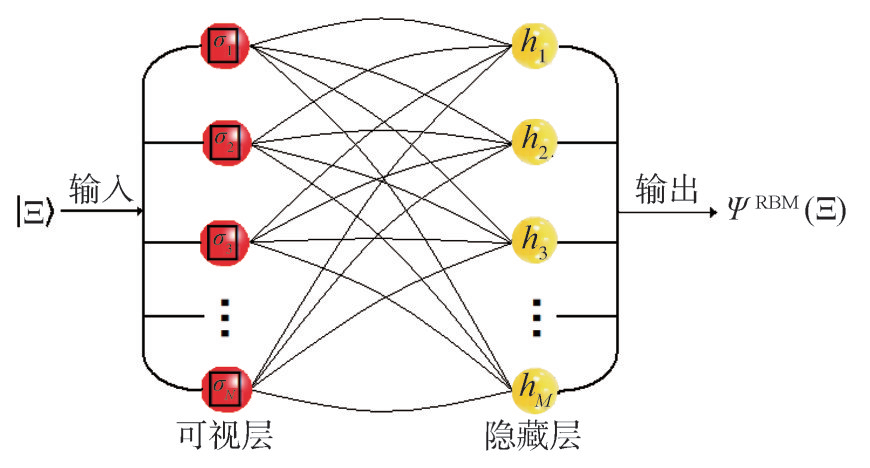
Restricted Boltzmann Machines (RBM) are a widely used type of neural network, with significant applications in data dimensionality reduction, feature learning, image generation, natural language processing, and more[18]. It is a two-layer neural network, where one layer is called the visible layer and the other is called the hidden layer. The neurons in the visible layer can connect to the hidden layer, but neurons within the same layer cannot connect to each other.
Consider a system composed of N quantum bits, where the general form of the quantum state is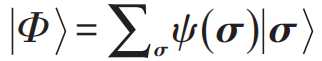 
, where σ = (σ1,σ2,⋯,σN) represents a possible configuration. ψ(σ) can be viewed as a function, with input σ and output being a complex number ψ(σ), representing the amplitude and phase information corresponding to the component 
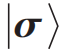. As shown in Figure 2, an RBM with N neurons in the visible layer (corresponding to N quantum bits) and M neurons in the hidden layer can be used to represent ψ(σ) [19]
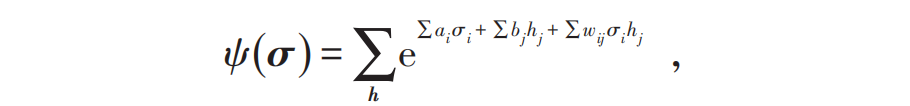
Where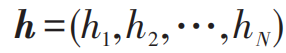 
represents the possible configurations of the hidden neurons, where each neuron can take two possible values σi = ±1 and hj = ±1, and ai, bj and wij represent the network’s biases and connection parameters, respectively. For simplicity, we refer to the quantum state represented by the restricted Boltzmann machine as the RBM state.
It can be mathematically proven that when M is sufficiently large, a restricted Boltzmann machine can approximate any smooth function to arbitrary precision. Therefore, in principle, the RBM representation of quantum states is complete, and any quantum state can be represented using a restricted Boltzmann machine. In practical applications, M generally increases polynomially with N, so the number of parameters required for the RBM to represent quantum states also increases polynomially with N, rather than exponentially. Thus, the RBM state may bypass the “exponential wall” difficulty when solving certain quantum many-body problems.
Unlike tensor network representations, restricted Boltzmann machines can effectively represent quantum states with large entanglement entropy[20]. This is due to the long-range connections between visible and hidden neurons. In fact, we can analytically construct an RBM state that satisfies the volume law of entanglement entropy (i.e., entanglement entropy is proportional to the volume of the subsystem), with the number of parameters contained increasing only linearly with N. In contrast, using conventional tensor network representations for the same quantum state would require the number of parameters to increase exponentially with N. This reflects the unique advantage of neural networks in representing quantum states with large entanglement entropy.
If we restrict that only neighboring visible neurons can connect to the same hidden neuron, this can further reduce the parameter scale and optimization difficulty, and the resulting quantum state is called the short-range RBM state. Due to this restriction, any visible neuron is only associated with its nearby neurons. Therefore, all short-range RBM states satisfy the area law of entanglement entropy.
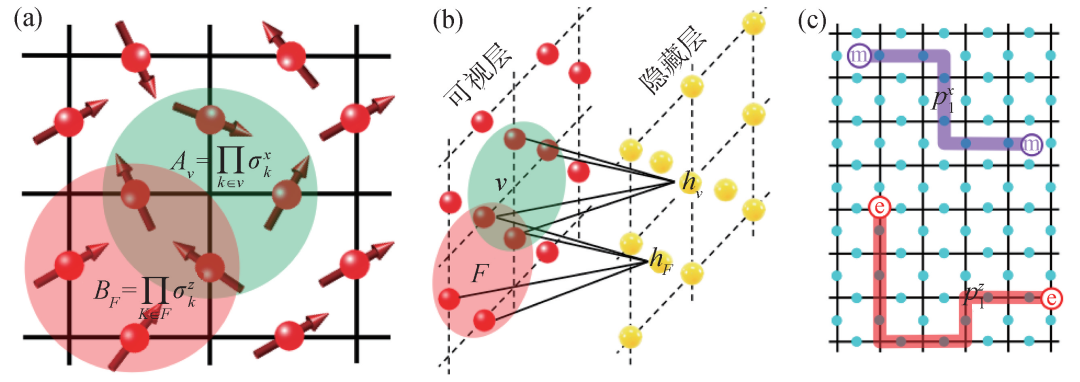
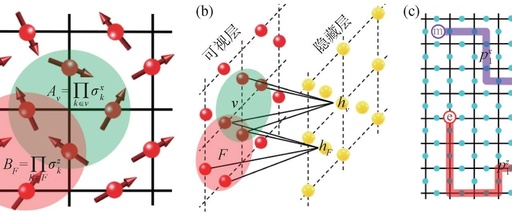
Figure 3 Restricted Boltzmann Machine Representation of Topological States (a) Toric Code Hamiltonian; (b) RBM Representation of the Ground State; (c) Excited State with 4 Anyons
We have discussed the RBM representation of pure states of quantum systems. In practice, quantum systems inevitably interact with their environment, and their states are mixed states that need to be described using density matrix operators. Restricted Boltzmann machines can also be used to represent mixed states[24]. It should be noted that to satisfy the requirements of the density matrix’s positive semi-definiteness, the parameters of the restricted Boltzmann machine representing mixed states must meet specific conditions. Additionally, by adding determinants or using Grassmann algebra methods, restricted Boltzmann machines can also be used to represent the quantum states of fermionic systems[25,26].
Restricted Boltzmann machines can effectively represent some interesting quantum states, but their expressiveness is limited. For example, they cannot effectively represent states that can demonstrate quantum supremacy, such as states obtained from two-dimensional cluster states through special unitary transformations[27]. This conclusion can be intuitively understood; due to the simple structure of the restricted Boltzmann machine, the quantum states it represents can be obtained through efficient algorithms. If it could effectively represent states that demonstrate quantum supremacy, it would imply that classical computers could efficiently simulate this quantum state, which contradicts the premise of the quantum supremacy of this state.
To enhance the expressive capacity of restricted Boltzmann machines, an additional hidden layer can be added to the original network, resulting in a network called a deep Boltzmann machine (DBM). In computational complexity theory, a widely accepted but yet unproven conjecture is that the polynomial hierarchy of complexity does not collapse; the famous P ≠ NP conjecture is a specific example of this conjecture. Assuming the above conjecture holds, it can be proven that DBMs can have exponential advantages in expressiveness compared to RBMs. There exist some quantum states that require exponential parameters to be represented by RBMs, while DBMs only require polynomial-scale parameters[28].
Feedforward neural networks are one of the earliest and simplest types of neural networks studied, and they are also among the most widely used and rapidly developing artificial neural networks[18]. Their neurons are arranged in layers, with each neuron only connected to the neurons in the previous layer. Information flows from the input layer to the output layer in a one-way manner without feedback. Similar to restricted Boltzmann machines, feedforward neural networks can also be used to represent quantum states[29]. The number of neurons in the input layer corresponds to the number of particles in the quantum system being considered, while the output layer consists of a single neuron that outputs a complex number, representing the amplitude and phase information corresponding to the quantum state.
For very complex quantum states, we can separate the wave function into two parts: the absolute value of the wave function and the corresponding sign, and use two feedforward neural networks to represent them separately. In practical applications, it can be observed that for simple quantum states, feedforward neural networks can accurately learn their corresponding sign rules; for some complex quantum states, feedforward neural networks can also learn with relatively high precision, confirming the effectiveness of using feedforward neural networks to process quantum states[29].
In the field of artificial intelligence, various neural networks have been designed for different problems, and in principle, all types of neural networks can be used to represent quantum states. Different networks have different structures, can effectively represent different quantum states, and have varying time complexities for training the networks. In practical applications, we can choose different neural networks based on specific problems[18]. For example, recurrent neural networks (RNNs) are very suitable for handling sequential data and are widely used in machine translation, speech recognition, and text generation. The configurations of quantum bits in many-body systems can be viewed as sequential data, allowing the use of recurrent neural networks to represent quantum many-body states[30]. Convolutional neural networks (CNNs) are another widely used type of deep neural network, suitable for scenarios such as image processing, behavior recognition, and transfer learning. Literature[31] indicates that convolutional neural networks can also be used to represent quantum states, such as the aforementioned toric code state.
As mentioned earlier, artificial neural networks can effectively represent many-body quantum states, and they have broad applications in quantum physics, especially in solving quantum many-body problems. Figure 4 summarizes the main applications of neural network quantum states. Next, we briefly introduce some recent related works, focusing mainly on the applications of RBM quantum states.
An isolated closed quantum system can be described by a Hamiltonian, and its evolution process satisfies the Schrödinger equation. Solving the ground state and dynamics of a given Hamiltonian is a common fundamental problem in quantum physics. For a few special models, such as the one-dimensional Ising model, the ground state and dynamics can be strictly solved analytically. However, in practical research, there are very few cases where the ground state and dynamics can be solved analytically, necessitating reliance on numerical methods.
The core idea of using neural networks to solve ground states and dynamics is to treat the neural network quantum state as a variational function and optimize the network parameters using gradient descent algorithms to solve the corresponding problem. Taking restricted Boltzmann machines as an example, G. Carleo and M. Troyer first solved the ground states and dynamics of several typical quantum magnetic models (such as the Ising model and Heisenberg model) and compared them with traditional methods like density matrix renormalization group[19]. The results show that the neural network methods achieved comparable precision for ground state energy and dynamic evolution with fewer parameters, demonstrating the superiority of neural network methods to some extent.
It is worth noting that solving the ground state and dynamic evolution for the most general cases can be proven to be NP problems. Therefore, neural network methods cannot effectively solve the ground states and evolution of all quantum systems. Current research indicates that they may have advantages over traditional methods in solving problems involving significant quantum entanglement and high-dimensional systems, but this advantage has not been definitively proven. How to determine whether the ground state and dynamics of a given Hamiltonian can be effectively solved using neural network methods is an important issue that needs to be addressed in this field. Solving this problem may require the development of new physical concepts and mathematical tools.
Out-of-time ordered correlators (OTOC) were first studied by A. Larkin and Y. Ovchinnikov in 1969 in the context of superconductivity[32]. After decades of development, OTOC has important applications in characterizing quantum chaos, quantum information scrambling, and dynamical phase transitions. Furthermore, it can provide new insights into quantum gravity and black holes through Ads/CFT duality. Recently, experimental measurements of OTOC have been achieved in systems such as ion traps, solid-state spins, and Bose-Einstein condensates.
Considering two local operators W and V that are spatially separated in a quantum many-body system, their corresponding OTOC is defined as
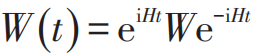
where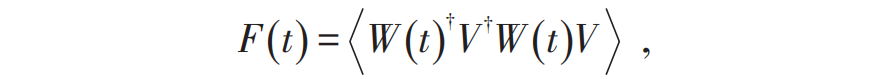
is the time evolution operator of W in the Heisenberg picture. It is not difficult to see that the physical significance of OTOC is to describe a local perturbation propagating over time and being detected elsewhere. Numerically calculating the OTOC for many-body systems is very challenging, and its complexity exceeds that of solving ground states or dynamic evolution. Literature[33] proposed a neural network approach to solve OTOC, with the core idea being to treat OTOC as the overlap of two quantum states evolving over time, thus solving it by calculating the evolution and overlap of the states.
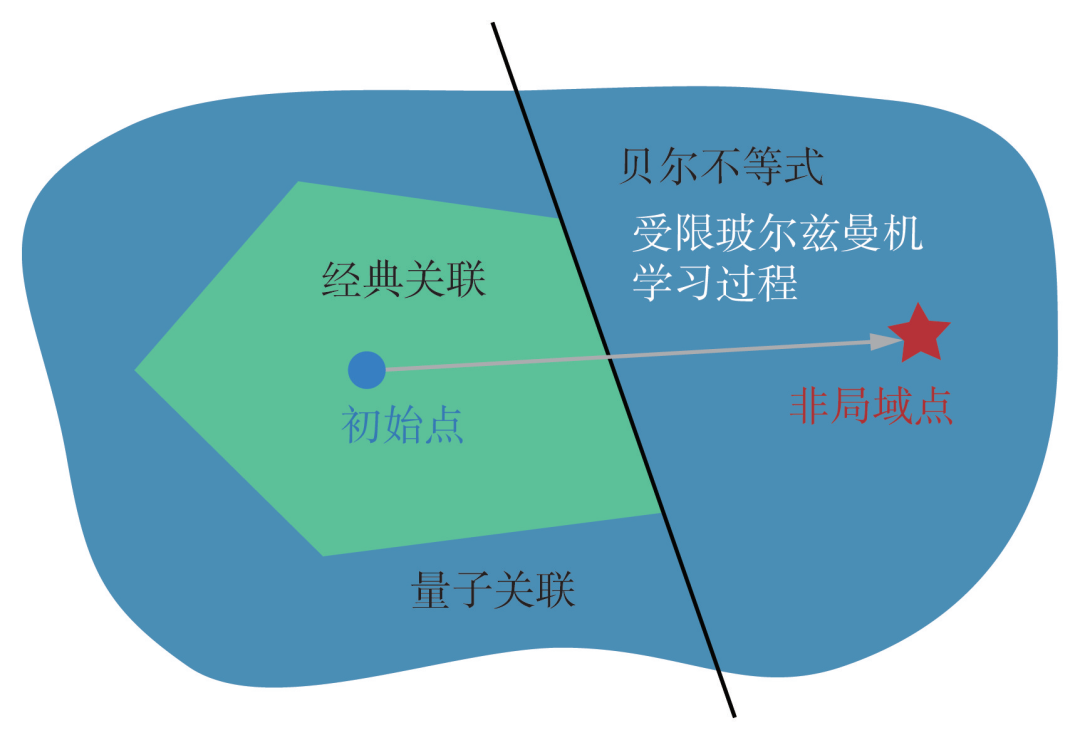
Nonlocality is a very peculiar property of quantum systems and is one of the core distinctions between quantum physics and classical physics[34]. It describes a stronger correlation than quantum entanglement—any quantum state that exhibits nonlocality must be entangled, but the converse is not necessarily true. In practical applications, quantum nonlocality is an indispensable resource for constructing device-independent quantum technologies, such as unconditionally secure quantum key distribution and self-testing random number generators. The contemplation and study of quantum nonlocality can be traced back to the famous debate between Einstein and Bohr in the early 20th century about whether “God plays dice”[35]. In 1964, John Stewart Bell (Figure 5) proposed the famous Bell inequalities[36]. Since then, quantum nonlocality can be quantitatively characterized by experimentally testing the violation of Bell inequalities.
However, due to the exponential wall difficulty, studying nonlocality in quantum many-body systems becomes extremely challenging. In literature[37], one of the authors of this article introduced machine learning methods into the study of quantum many-body nonlocality. The core idea is to transform the problem of detecting nonlocality in quantum many-body systems into the problem of solving the ground state energy of the Hamiltonian, allowing the use of the aforementioned neural network quantum state methods to handle it. Specifically, for a given quantum many-body system, all possible classical correlations compose a polytope in high-dimensional space, with each face of the polytope corresponding to a Bell inequality, as shown in Figure 6. Initially, we randomly generate an RBM quantum state, which generally exhibits only classical correlations for a given observable. By continuously optimizing the parameters of the RBM, the represented quantum state gradually surpasses one face of the polytope (i.e., violating the corresponding Bell inequality), demonstrating quantum nonlocality. It is worth noting that neural network quantum states have unique advantages in detecting many-body nonlocality problems, being able to solve some problems that are difficult or impossible to solve with traditional methods, such as calculating the maximum violation of Bell inequalities in random fully entangled systems.
Isolated quantum systems evolve according to the Schrödinger equation, while practical systems inevitably interact with their environment; therefore, many cases cannot be treated as isolated systems. For open systems that are weakly coupled to the environment, the evolution of their states can be approximated as being dependent only on the current state and not on the previous evolution process. Consequently, using the Born-Markov approximation, we can derive the evolution equations satisfied by open systems, namely the Lindblad master equation[38]:
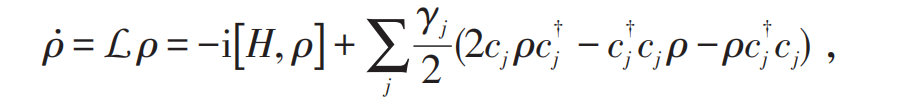
where L is the Liouvillian superoperator, H is the system Hamiltonian, ρ is the density matrix, and cj and γj represent the dissipative operators and dissipation strengths, respectively.
Similar to isolated systems, neural network methods can also be used to solve the steady states and dynamic evolution of open quantum systems, where the neural network representation of the density matrix is required[24]. Unlike isolated systems, the energy of open quantum systems is no longer a conserved quantity; therefore, it cannot be solved by variational methods based on energy. However, we can consider optimizing the distance between variational approximate evolution and exact evolution or transforming the master equation into an effective Hamiltonian equation through Choi-Jamiołkowski isomorphism to solve it. Relatedly, we further generalized the neural network methods to solve the Liouvillian gap[39].
Quantum state tomography is a technique for estimating an unknown quantum state by measuring many identical quantum states[15]. It is an important technique for calibrating quantum systems and verifying quantum operations. Similarly, due to the exponential increase in the dimension of the Hilbert space with system size, quantum state tomography for many-body systems becomes extremely challenging. For example, in the 2019 experiment by Google that achieved quantum supremacy[40], the quantum circuit involved 53 quantum bits, and the most direct method for such large-scale quantum state tomography would require determining approximately 253 ≈1016 parameters; even storing these parameters would require at least 105 TB of storage space, far exceeding the memory capacity of the most advanced supercomputers available today.
Neural networks can effectively represent some quantum states, with the number of required parameters increasing polynomially with system size. Therefore, performing quantum state tomography using neural networks only requires determining parameters on a polynomial scale, significantly reducing the required resources. In fact, neural network quantum state tomography has already been proposed in several papers[30,41] and has received considerable attention. Recently, some related theoretical schemes have also been experimentally validated[42].
Neural network quantum states are a rapidly developing interdisciplinary frontier direction in recent years. Currently, research in this direction has achieved some exciting results. However, overall, its development is still in its early stages, and many important fundamental problems remain to be solved. First, the effectiveness and limitations of neural networks in expressing quantum states are not fully understood. Given a quantum state, we cannot effectively determine whether it can be expressed using a specific neural network. This is similar to the early development of matrix product states or broader tensor network states. Due to the rapid development in the field of quantum information, we now know that quantum entanglement is the key to tensor networks effectively representing quantum states and is also a prerequisite for judging whether specific problems can be effectively solved using relevant algorithms. However, quantum entanglement is not the core element of neural networks expressing quantum states; understanding the effectiveness and limitations of neural networks may require the development of new physical concepts and mathematical tools. Secondly, the