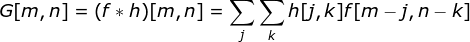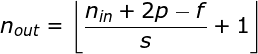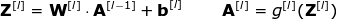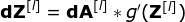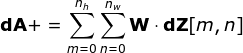This article shares an analysis of the mathematical principles of CNNs, which will help you deepen your understanding of how neural networks work in CNNs. As a recommendation, this article will include quite complex mathematical equations; if you are not familiar with linear algebra and calculus, that’s okay. The goal is not to memorize these formulas but to have an intuitive understanding of what is happening below.
Complete source code with visualization and annotations:
GitHub: https://github.com/SkalskiP/ILearnDeepLearning.py
Introduction
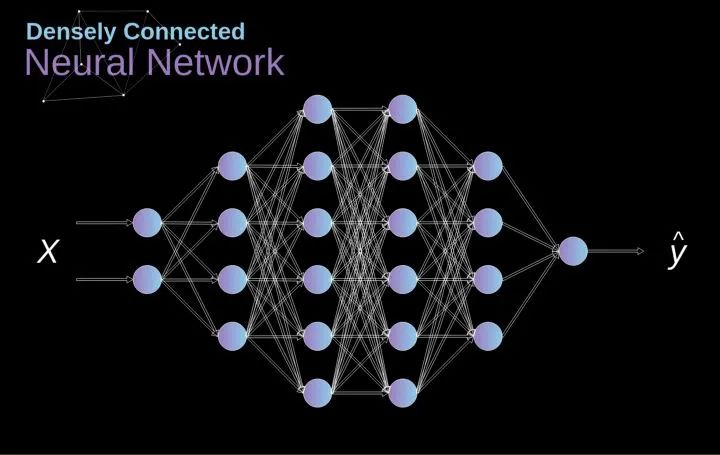
In the past, we have learned about these densely connected neural networks. The neurons in these networks are grouped into several layers, forming continuous layers. Each such neuron is connected to every neuron in the adjacent layer. The figure below shows an example of this architecture.
Figure 1. Structure of a densely connected neural network
This approach is effective when we solve classification problems based on a set of finite, artificially designed features. For example, we predict a football player’s position based on statistics during the game. However, when dealing with photos, the situation becomes more complex. Of course, we can treat the pixel values of each pixel as separate features and pass them as inputs to our dense network.
Unfortunately, to make this network applicable to a specific smartphone photo, our network would need to contain tens of millions or even hundreds of millions of neurons. On the other hand, we could downscale our photos, but in the process, we would lose some useful information.
We immediately realize that traditional strategies do not work for us, and we need a new effective method to make the most of as much data as possible while reducing the necessary computation and number of parameters. This is where CNNs come into play.
Data Structure of Digital Images
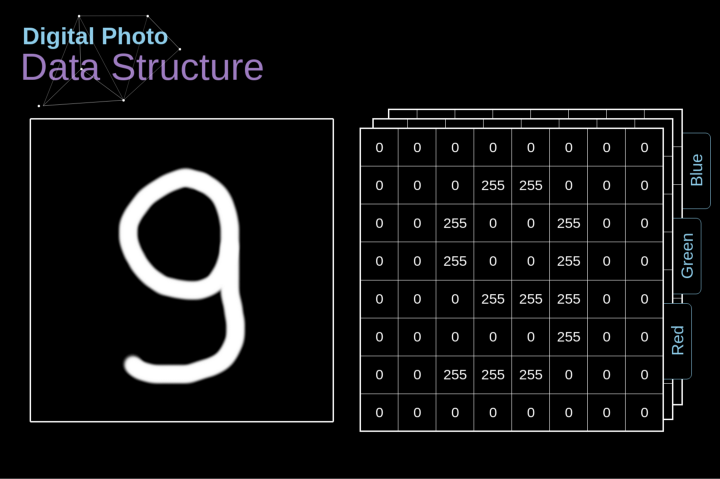
Let’s take a moment to explain how digital images are stored. Most of you may know that they are actually composed of a matrix of many numbers. Each of these numbers corresponds to the brightness of a pixel. In the RGB model, a color image is actually composed of three matrices corresponding to the red, green, and blue color channels.
In a black-and-white image, we only need one matrix. Each matrix stores values between 0 and 255. This range is a compromise between the efficiency of storing image information (256 values can be represented by one byte) and the sensitivity of the human eye (we distinguish a limited number of the same color grayscale values).
Figure 2. Data Structure of Digital Images
Convolution kernels are not only used in neural networks but are also a key component of many other computer vision algorithms. In this process, we take a smaller matrix (called a kernel or filter) and input the image, transforming the image based on the values of the filter. The subsequent feature map values are calculated according to the following formula, where the input image is represented by f, our kernel by h, and the row and column indices of the resulting matrix by m and n, respectively.
Figure 3. Example of Kernel Convolution
After placing the filter over a selected pixel, we extract the values from the kernel at each corresponding position and multiply them pairwise with the corresponding values in the image. Finally, we sum everything and place the result at the corresponding position in the output feature map.
Above, we can see how such an operation is implemented in detail, but what is more concerning is what applications we can achieve by performing kernel convolution over a complete image. Figure 4 shows the convolution results of several different filters.
Figure 4. Edge Detection through Kernel Convolution [Original Image: https://www.maxpixel.net/Idstein-Historic-Center-Truss-Facade-Germany-3748512]
Valid Convolution and Same Convolution
As shown in Figure 3, when we convolve a 6×6 image with a 3×3 kernel, we obtain a 4×4 feature map. This is because there are only 16 different positions where we can place the filter in this image. Since the image shrinks with each convolution operation, we can only perform a limited number of convolutions until the image completely disappears.
More importantly, if we observe how the convolution kernel moves in the image, we find that the impact of pixels located at the edges of the image is much smaller than that of pixels located in the center of the image. Thus, we lose some information contained in the image. The following figure shows how the position of the pixel changes its influence on the feature map.
Figure 5. Influence of Pixel Position
To solve these two issues, we can pad the image with extra borders. For example, if we use a 1px padding, we increase the size of the photo to 8×8, and the output of the convolution with a 3×3 filter will be 6×6. In practice, we usually use 0 to fill the extra padding area. Depending on whether we use padding, we will judge based on two types of convolutions – valid convolution and same convolution.
This naming is not very appropriate, so for clarity: Valid means we only use the original image, Same means we also consider the surrounding borders of the original image, so the size of the input and output images is the same. In the second case, the padding width should satisfy the following equation, where p is the padding width and f is the filter dimension (usually odd).
Stride Convolution
Figure 6. Example of Stride Convolution
In the previous examples, we always moved the convolution kernel one pixel at a time. However, the stride can also be seen as one of the hyperparameters of the convolution layer. In Figure 6, we can see what the convolution looks like if we use a larger stride.
When designing the CNN architecture, if we want less overlap in the perceptive field or want a smaller spatial dimension of the feature map, we can decide to increase the stride. The size of the output matrix – considering the padding width and stride – can be calculated using the following formula.
Transition to Three Dimensions
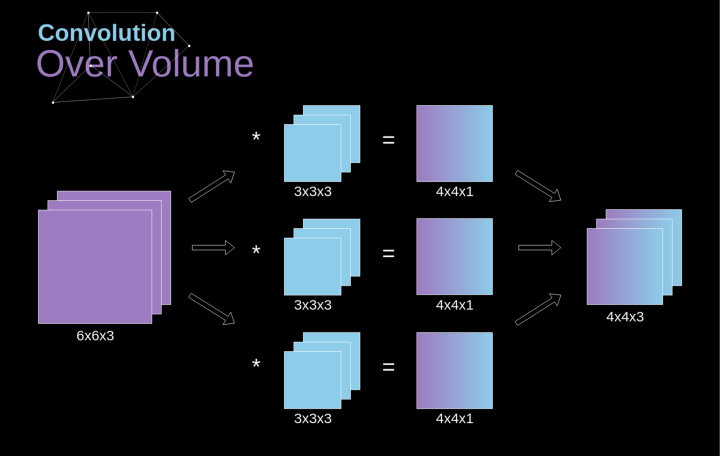
Spatial convolution is a very important concept, as it allows us to process color images and, more importantly, apply multiple convolution kernels within a single layer. The first important principle is that the filter and the image to which it is applied must have the same number of channels. Basically, this method is very similar to the example in Figure 3, except this time we multiply the values in three-dimensional space with the corresponding convolution kernels.
If we want to use multiple filters on the same image, we convolve them separately, stack the results, and combine them into one whole. The dimensions of the receiving tensor (i.e., our three-dimensional matrix) satisfy the following equation: n – image size, f – filter size, nc – number of channels in the image, p – whether padding is used, s – stride used, nf – number of filters.
Figure 7. Three-Dimensional Convolution
Convolution Layer
Now it’s time to apply what we’ve learned today to build our CNN layers. Our approach is almost the same as what we used in densely connected neural networks, the only difference being that this time we will use convolution instead of simple matrix multiplication.
Forward propagation involves two steps.
The first step is to calculate the intermediate value Z, which is obtained from the convolution of the input data and the weight tensor W of the previous layer (including all filters), then adding the bias b.
The second step is to apply the nonlinear activation function to the obtained intermediate value (our activation function is denoted as g). Readers interested in the matrix equation can find the corresponding mathematical formulas below. By the way, in the following figure, you can see a simple visualization describing the dimensions of the tensors used in the equation.
Figure 8. Tensor Dimensions
Connection Pruning and Parameter Sharing
At the beginning of the article, I mentioned that densely connected neural networks are not good at processing images because they require learning a large number of parameters. Now that we understand what convolution is, let’s consider how it optimizes computation.
In the figure below, the two-dimensional convolution is shown in a slightly different way, with neurons numbered 1-9 forming the input layer and receiving the brightness values of the image pixels, while units A – D represent the computed feature map elements. Finally, I-IV are the values of the convolution kernels that need to be learned.
Figure 9. Connection Pruning and Parameter Sharing
Now, let’s focus on two very important properties of the convolution layer.
First, you can see that not all neurons in two consecutive layers are connected to each other. For example, neuron 1 only affects the value of A.
Secondly, we see that some neurons share the same weights. These two properties mean that we need to learn far fewer parameters.
By the way, it is worth noting that one value in the filter affects every element in the feature map – this is very important during backpropagation.
Backpropagation in Convolutional Layers
Anyone who has ever tried to write their own neural network code from scratch knows that completing forward propagation does not complete half of the entire algorithm process. The real fun begins when you want to perform backpropagation. Now, we do not need to be troubled by this issue of backpropagation; we can leverage deep learning frameworks to implement this part, but I think understanding the underlying concepts is valuable. Just like in densely connected neural networks, our goal is to compute the derivatives and then use them to update our parameter values, a process called gradient descent.
In our calculations, we need to use the chain rule – I mentioned this in a previous article. We want to evaluate how changes in parameters affect the final feature map and subsequently the final results. Before we start discussing the details, let’s unify the mathematical notation used – to simplify the process, I will forgo the complete notation of partial derivatives and use a shorter notation as shown below. But remember, when I use this notation, I always refer to the partial derivatives of the loss function.
Figure 10. Forward and Backward Propagation of a Single Convolution Layer
Our task is to compute dW[l] and db[l] – which are the derivatives related to the parameters of the current layer – and the value of dA[l -1] – which will be passed to the previous layer. As shown in Figure 10, we receive dA[l] as input. Of course, the dimensions of the tensors dW and W, db and b, and dA and A are the same. The first step is to obtain the intermediate value dZ[l] by taking the derivative of the activation function of the input tensor. According to the chain rule, this operation will be used to obtain results later.
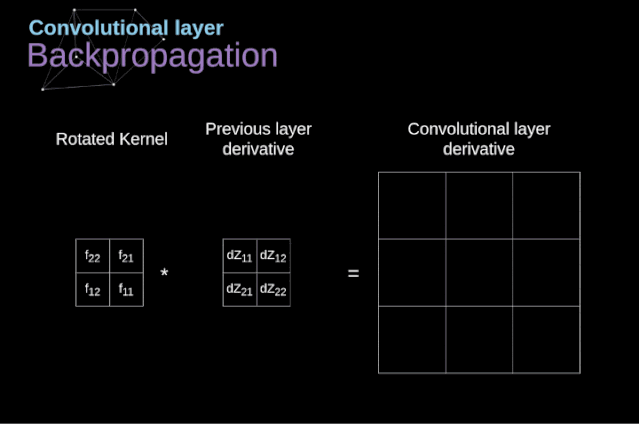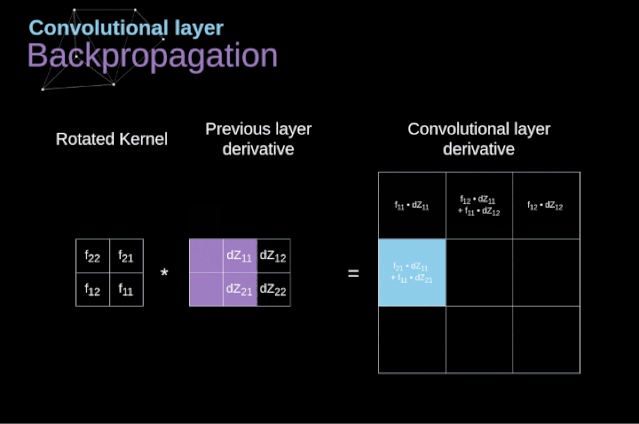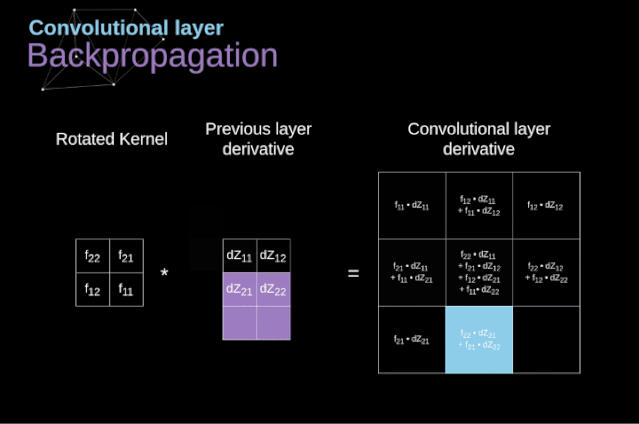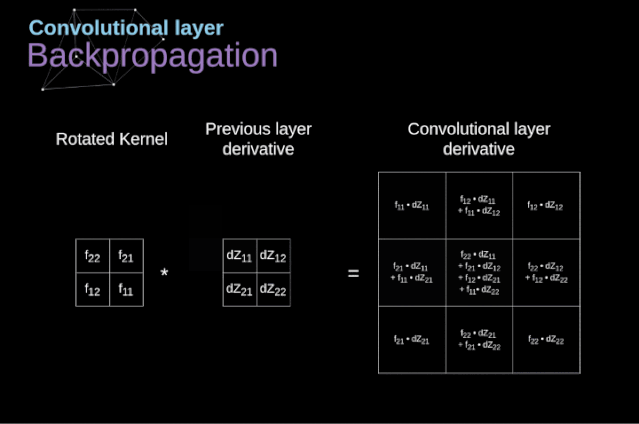
Now, we need to handle the backpropagation of the convolution itself. To achieve this, we will use a matrix operation called full convolution, as shown in the figure below. Note that in this process, we rotate the convolution kernel by 180 degrees before using it. This operation can be described by the following formula, where the filter is represented by W, and dZ[m,n] is a scalar belonging to the partial derivative of the previous layer.
Figure 11. Full Convolution
In addition to convolution layers, CNNs also frequently use what is called a pooling layer. Pooling layers are mainly used to reduce the size of the tensor and accelerate computation. This type of network layer is simple – we need to segment the image into different regions and then perform some operations on each part.
For example, for a max pooling layer, we select the maximum value from each region and place it in the corresponding position in the output. In the case of convolution layers, we have two hyperparameters – filter size and stride. One last important point is that if pooling operations are to be performed on multi-channel images, they should be performed separately for each channel.
Figure 12. Example of Max Pooling
Backpropagation in Pooling Layers
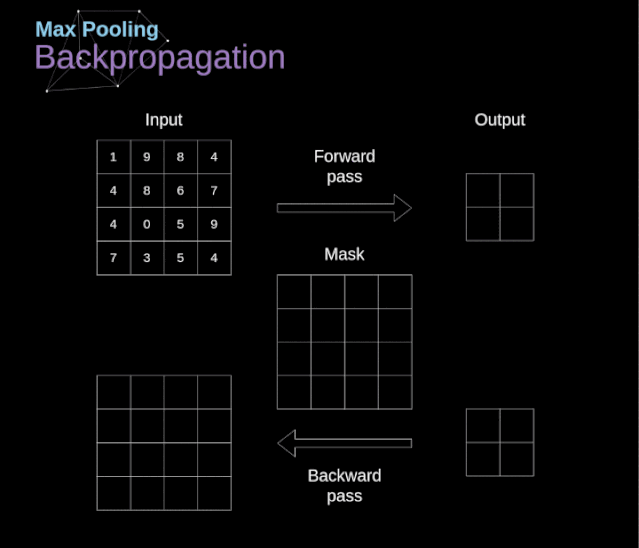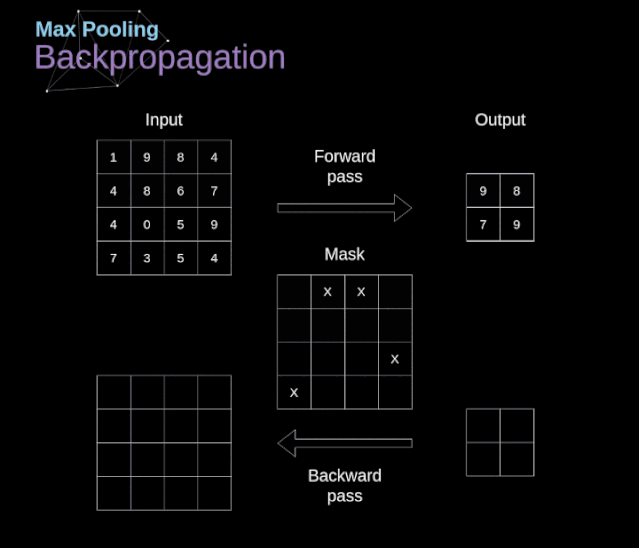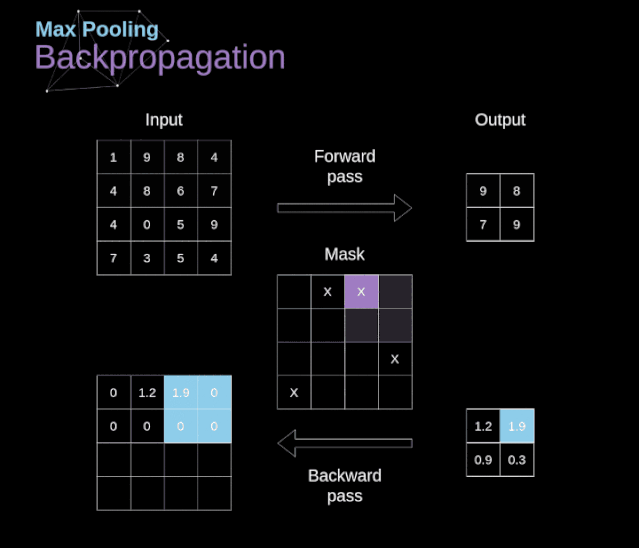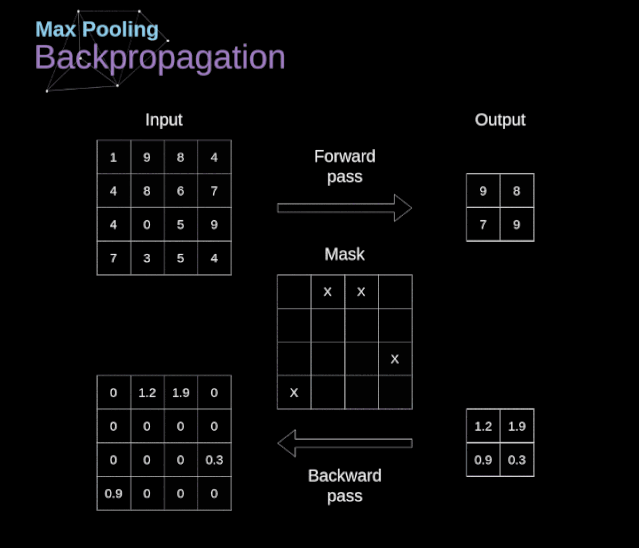
In this article, we will only discuss the backpropagation of max pooling, but the rules we learn only need slight adjustments to apply to all types of pooling layers. Since there are no parameters to update in this type of layer, our task is simply to distribute the gradients appropriately. As we remember, during the forward propagation of max pooling, we select the maximum value from each region and pass them to the next layer.
Therefore, it is clear that during backpropagation, the gradients should not affect the elements in the matrix that were not included in the forward propagation. In fact, this is achieved by creating a mask that remembers the positions of the values used in the first stage, which we can later use to propagate the gradients.
Figure 13. Backpropagation of Max Pooling
Reference: https://towardsdatascience.com/gentle-dive-into-math-behind-convolutional-neural-networks-79a07dd44cf9
Source: Turing Artificial Intelligence, This article is for academic sharing only, copyright belongs to the original author. If there is any infringement, please contact WeChat: 1306859767, Eternalhui, for deletion or modification!
Previous Highlights:
Normal Distribution is Important for Data Analysis!
The French Revolution and Mathematics
What Mathematics Taught Me?