Machine Learning: From Priors to Automation

Artificial intelligence, represented by deep learning, has crossed the technological tipping point from “not usable” to “usable”; however, there is still a long way to go from “usable” to “very usable”. The core technology of artificial intelligence is machine learning, which summarizes patterns or seeks representations from a given dataset, summarized in the formula shown in Figure 1.

This model summarizes the general steps in solving problems with machine learning: First, we need to select a broad range of hypothesis space that may contain data patterns or representation functions, then specify a loss metric under which we find a function in the hypothesis space that minimizes the average loss on the given dataset. The goal of minimizing the average loss on the dataset is called the “data fitting term”, and the corresponding method is empirical risk minimization. However, merely minimizing the data fitting term to find a solution is often ill-posed, so certain additional constraints must be added, and these additional constraints we hope to satisfy constitute the “regularization term”. The minimization of the sum of the data fitting term and the regularization term is called the “regularization method”, which constitutes the most basic model of machine learning.

When using machine learning, we always consciously or unconsciously impose some assumptions, such as:

Independence Assumption of Loss Metric. We always tend to use deterministic metrics like least squares or cross-entropy as the loss, without linking the choice of loss metric to the specific problem we are trying to solve, nor do we adaptively determine the optimal loss metric based on the problem at hand.

Assumption of High Capacity of Hypothesis Space. We naturally assume that the machine architecture we choose (for example, a 20-layer deep learning architecture) already contains the solution we hope to find or, in other words, already encompasses the patterns contained in the data. This assumption is evidently a prerequisite for the success of machine learning. We are usually quite confident that the architecture we select is reasonable and contains the solution we are looking for.

Completeness Assumption of Training Data. When using machine learning, we always expect the data used to train the machine to be very sufficient, abundant, and high-quality. This assumption often serves as the premise and reason for our choice of machine learning methods.

Prior Determinism Assumption of Regularization Terms. To ensure that the decision function produced by machine learning has the desired properties, it is necessary to impose certain regularization constraints. For example, we are accustomed to using L2 regularization to ensure smoothness, L1 regularization to guarantee sparsity, TV regularization to maintain image edge sparsity, etc. It is generally believed that the form of the regularization term is predetermined by prior knowledge, and when using machine learning, we can determine it based on prior knowledge. The essence of this assumption is that we have already abstracted prior knowledge of the problem and can correctly model it in the form of “regularization terms”. This understanding is called an assumption because we do not actually know whether the regularization term chosen in practice has correctly modeled the prior.

Euclidean Assumption of Analytical Framework. When training deep network architectures, we naturally choose to use optimization algorithms like BP or ADAM. Why? This is because these algorithms have undergone rigorous theoretical evaluation (convergence, stability, complexity, etc.). Evaluating algorithms involves placing algorithms within a specific mathematical framework for analysis to draw conclusions. We typically evaluate algorithms within Euclidean frameworks that utilize norms and orthogonality. This assumption essentially limits the types of algorithms that can be used and the architectures of machines that can be employed (loss functions, regularization terms, etc.). Under such assumptions, we cannot handle or dare to use more complex non-Euclidean algorithms and machine learning architectures.

These five assumptions largely determine the effectiveness of machine learning.

A significant amount of work has focused on how to overcome these assumptions in machine learning. Below are some representative works by the author’s team in recent years in this regard.

About the Euclidean Assumption of Analytical Framework

We believe that the widespread use of Euclidean space is fundamentally due to our ability to use Euclidean architectures in algorithm analysis ((a+b)²=a²+b² +2ab), under such architecture, the performance of any algorithm (such as convergence) is related to the convexity of the objective function. Therefore, breaking the convexity assumption of the objective function essentially means breaking the Euclidean assumption. The author’s work in 1989 and 1991 opened up the possibility of studying non-Euclidean algorithms using non-Euclidean architectural tools, which have been widely applied in recent years. From these studies, it can be seen that the pathway to breaking the Euclidean assumption lies in applying Banach space geometry.

About the Independence Assumption of Loss

Loss has two functions: one is to measure the degree of fit of the selected function on the given data/dataset, and the other is to measure the accuracy represented by a function. Although they may have different forms in supervised and unsupervised learning modes, their selection should essentially be related to the problem. In fact, if we understand the label and features of the problem using the observation model described in Equation (1),

y=f_θ(x)+e (1)

Then, the label is obtained from a fixed pattern plus noise, and this noise is the environment of data acquisition. According to probability formulas, we can easily see that the probability of the best label appearing is entirely determined by its error environment. This gives us an important insight: the best metric for machine learning should be determined by the error. Through experiments, we find that if we assume the error is white noise, then the optimal recovery metric is indeed least squares. However, if the noise is of another type, the optimal recovery metric will no longer be least squares.

Given a specific form of error distribution, we can determine a specific optimal recovery metric, and this method is called the error modeling principle. For any machine learning problem, by studying the form of the error it generates, we can obtain the optimal loss metric in a certain sense, and finding the empirical function of machine learning under that metric is the best. The author’s team has many successful applications of the error modeling principle, the most typical being the successful development of micro-dose CT based on this principle, achieving a reduction in CT radiation dose to micro-dose levels.

In general, we do not know what kind of error environment the problem to be solved is in. In this case, we can use Gaussian mixtures to approximate. In fact, any fractional function can be approximated by the sum of multiple Gaussian distribution functions. Based on this, we prove that different Gaussian mixtures lead to differently weighted “weighted least squares” optimal metrics. This gives a very useful hint: when we do not know the true form of the error, weighted least squares is a good choice.

About the High Capacity Assumption of Hypothesis Space

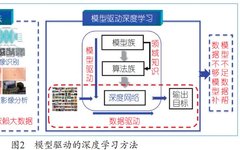
How to design a machine architecture so that the hoped-for solution to the problem is indeed contained within it? We propose a very fundamental method: first construct a rough model containing a large number of hyperparameters (called a model family) to characterize the range of problem solutions, then solve the “model family” to form the “algorithm family” that solves the problem, and finally adaptively expand the “algorithm family” into a deep network architecture, whose parameters include all parameters from the model family and algorithm family and allow different parameters at each iteration step; finally, apply data to train the network formed in this way to produce the solution to the problem. This generalization method is called model-driven deep learning. Model-driven deep learning superficially seems to solve the architecture design problem of deep learning, but essentially it gradually sets the minimum hypothesis space containing the solution during the deep learning process to break through the high capacity assumption of hypothesis space. This method is different from traditional mathematical modeling methods (which require precise modeling); the former only requires characterization of the overall range of problem solutions; it is also different from traditional deep learning (which does not incorporate physical mechanisms), model-driven deep learning has clear physical mechanism explanations and rigorous mathematical foundations. Thus, it avoids the difficult problem of deep learning architecture design, allowing machine learning architectures to be designed under theoretical guidance and interpretable meanings, as shown in Figure 2.

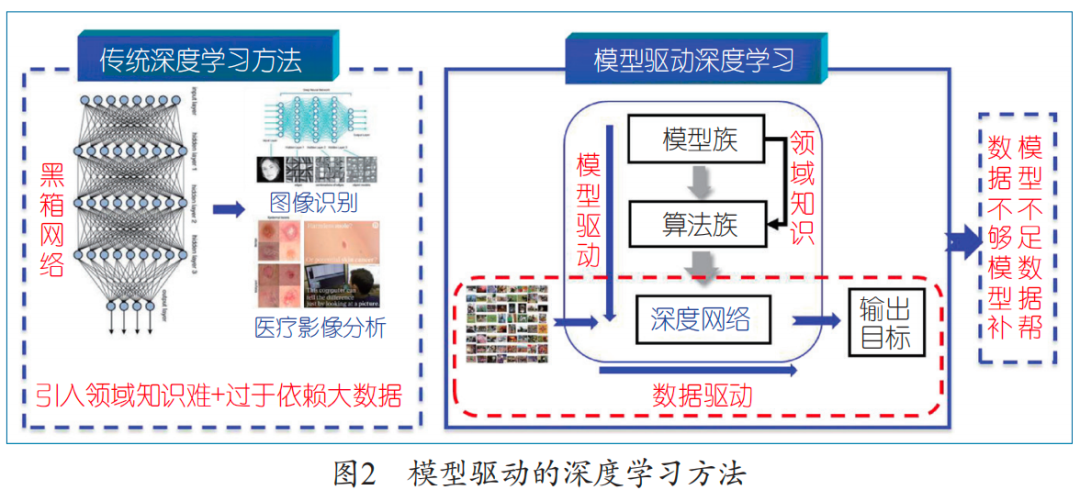
In 2018, the author’s team formally proposed this method in the National Science Review (NSR). Using this method, the author’s team proposed the well-known ADMM CS-Net deep learning architecture. This architecture is a universally effective deep learning model for achieving compressed sensing and has been widely applied, being regarded as a pioneering and foundational network. Its significance lies in building a bridge between optimization theory and deep learning network design, especially as it can better handle sparsity issues than traditional compressed sensing models and regularization methods.

About the Prior Determinism Assumption of Regularization Terms

Breaking the prior assumption of regularization is very difficult because no matter how we choose, we cannot guarantee that the selected regularization term truly reflects the prior. We analyze that the difficulty of the problem lies in the “regularization method is modeling the prior at the knowledge level”; to escape this predicament, the solution is to learn the prior directly from the data. To this end, we propose and establish a method called “implicit regularization theory”. We prove that under certain conditions, the solution to the regularization problem can be equivalent to a fixed-point equation containing a proximal projection operator, which can naturally be iteratively solved and expanded into a model-driven deep learning network, and the proximal projection operator and the regularization term can uniquely determine each other. Thus, instead of setting regularization terms, we can learn the proximal projection operator from the data, achieving the same effect as regularization methods. Notably, setting regularization terms utilizes prior knowledge, while implicit regularization extracts knowledge from data and integrates it into the learning process, thus having significant implications in principle.

About the Completeness Assumption of Data

The completeness and high quality of data are key to ensuring the effectiveness of machine learning. The idea of curriculum learning can analogize the learning process to the process of human education, thus addressing incomplete data in a stepwise manner (just as elementary school students first learn simple content before moving on to more difficult content). Over the past decade, the author’s team has completely established a theoretical and algorithmic system for “curriculum self-paced learning”, standardizing curriculum learning into a highly effective machine learning method for handling incomplete data.

In summary, our work over the past few years has been to develop some scientific principles, hoping that under the guidance of these principles, the prior assumptions of machine learning can be overcome. Our work mainly includes: using Banach geometric tools to break the Euclidean assumption of analysis, using the error modeling principle to break the independence assumption of loss, using model-driven deep learning to break the high capacity assumption of hypothesis space, using implicit regularization methods to break the prior assumption of regularization, and using curriculum self-paced learning to break the completeness assumption of data (see Figure 3). All these works have proven to be very effective.

The current development of machine learning is still largely in the “manual” stage: at the data level, manual collection and labeling of data are still required, and it is necessary to manually decide which data to use for training and which for testing; at the model and algorithm level, people mostly just choose an architecture and algorithm from known models and algorithms, essentially remaining in a passive selection state; at the application level, we still handle one task with one model, unable to achieve task switching and environmental adaptation. Clearly, to push artificial intelligence from “manual” to “autonomous”, a critical step must be taken, namely, machine learning must become “automated”, as illustrated in Figure 4.

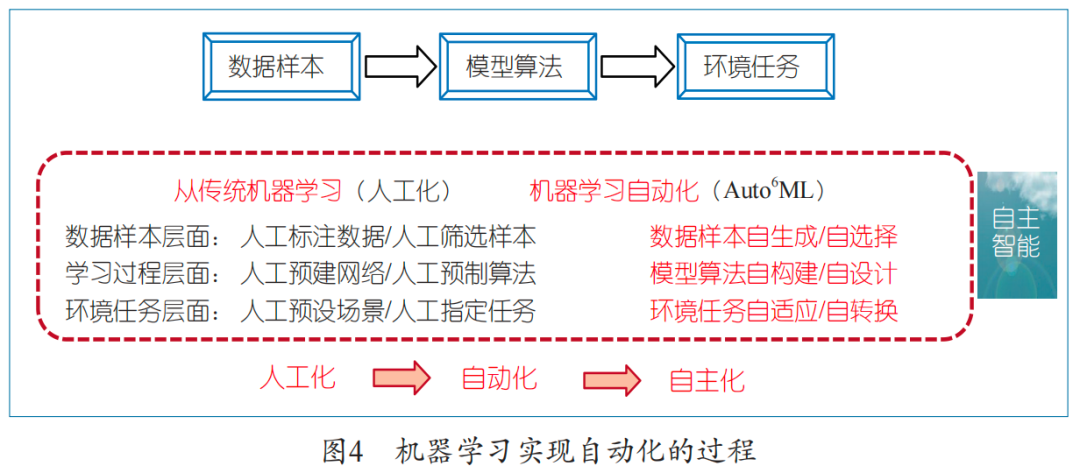
We believe that machine learning automation must first achieve at least six aspects of automation. First, data automation: achieving self-generation and self-selection of data. It should automatically generate training data based on the needs of target tasks or a small amount of metadata (standard, high-quality data) and automatically select samples suitable for learning from massive non-high-quality data; Second, architecture/algorithm automation: achieving self-construction of network architecture and self-design of training algorithms. It should automatically parse and assemble the “functional blocks” needed to complete the task in an optimal way (as simply and even minimally as possible) to form the required deep network architecture; Third, application/update automation: achieving self-adaptive setting of loss metrics according to problems (data) and self-adaptive setting of regularization terms, enabling the adaptive construction and selection of network training algorithms; achieving task switching and environmental adaptation. To realize a machine learning system that can complete multiple tasks with one architecture and switch automatically, it must be capable of continuous learning, autonomous evolution, and adaptive completion of new tasks.

We refer to machine learning that can achieve these six “automation” objectives as “automated machine learning”. Clearly, we are still in the manual stage of machine learning, but we are moving towards automation and autonomy. It is essential to recognize the significant meaning and value of achieving automation in machine learning, as it is not only a necessary path to achieving autonomous intelligence but also a practical demand for promoting the development and application of artificial intelligence.

How to achieve automation in machine learning? On the surface, it involves the design issues of various elements of machine learning (such as hypothesis space, loss function, regularization term, learning algorithm, etc.), but essentially it involves the learning methodology of learning. Here we propose a framework of Simulate Learning Methodology (SLeM) as shown in Figure 5, and explain how to achieve machine learning automation through SLeM.

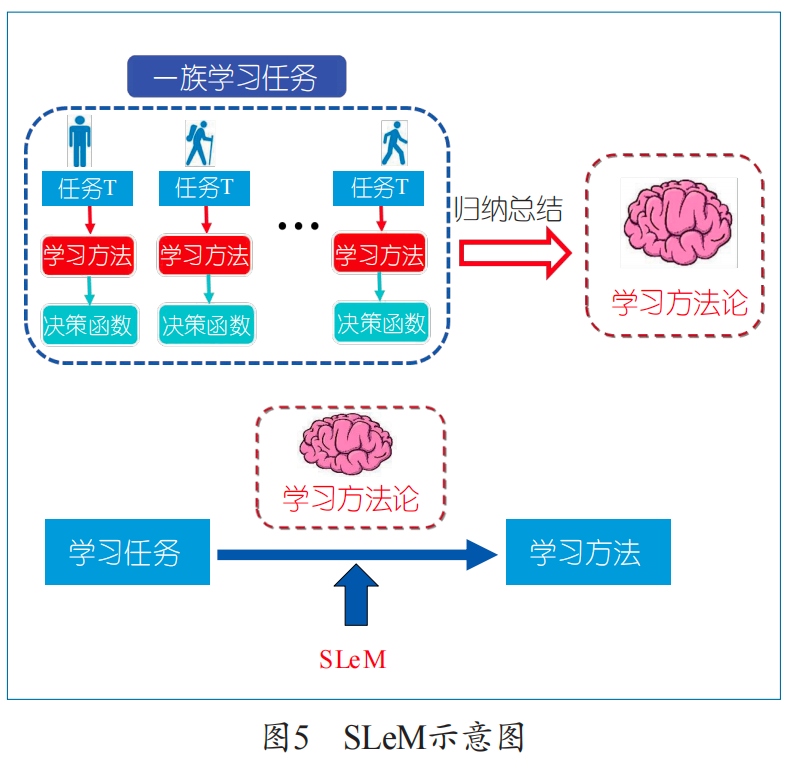
Learning methodology is a general principle and methodology that guides and manages learners on how to learn. To establish the SLeM framework, we need to strictly mathematically define concepts such as learning tasks, learning methods, and learning methodologies.

Learning Task

The purpose of learning is to summarize and characterize observable laws of the real world. We believe that a law of the real world can be described by a random variable or equivalently by a distribution function (density function). Sampling a random variable (the law of the real world) in different spatiotemporal contexts manifests as data reflecting the same law in different spacetime (these typically constitute the objects of machine learning research). Learning from data can manifest as classification, regression, dimensionality reduction, latent variable identification, etc., but essentially it is learning the distribution behind the data (as long as the distribution is known, all specific tasks can be represented by the distribution function). Therefore, the learning task should be defined as a statistical “density estimation problem”, which is to determine the distribution (density function) of the random variable behind the data given the data. The essence of learning is to summarize and characterize a law of the observable real world.

Learning Method

Based on the previous analysis of machine learning elements, as long as a specific set of “data generation methods, hypothesis space/machine architecture, loss metrics, optimization algorithms” is specified, it can be considered that a learning method has been defined. Thus, we define a learning method as a specified set K=(D, f, L, A), where D is the data generation method, f is the machine architecture, L is the loss metric, and A is an optimization algorithm that can be used for training. Here, the learning space K is naturally defined as the product of distribution function space, hypothesis space, loss function space, and optimization algorithm space, as shown in Figure 6.

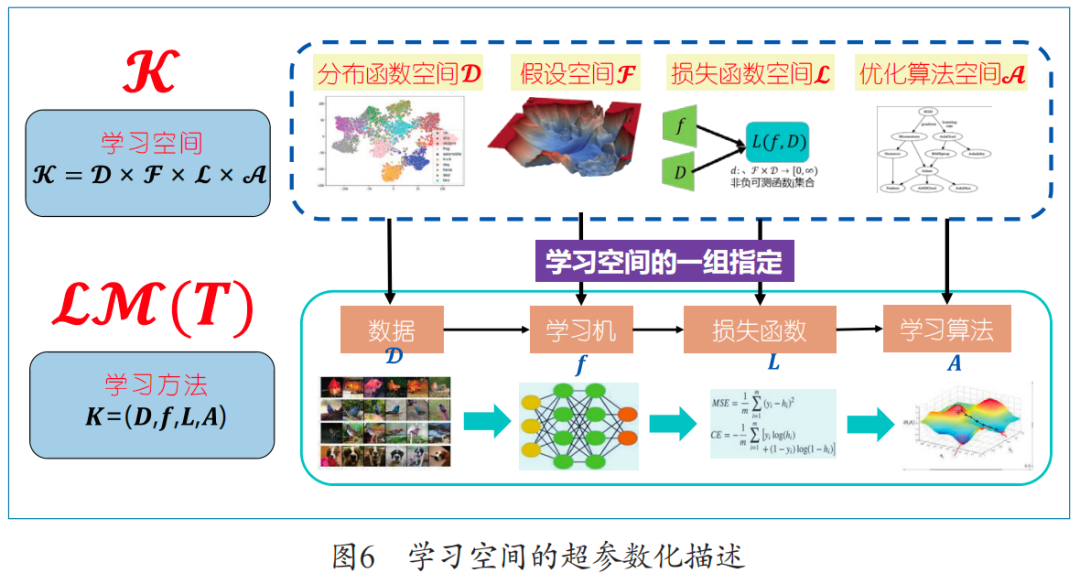
The learning space K is evidently infinite-dimensional. However, if we assume that each factor space of K has a countable basis (which naturally holds in applications, for example, different means and variances of Gaussian distributions constitute a countable basis for the distribution function space), then the learning space K can be serialized (i.e., isomorphic to a sequence space), corresponding to four infinite sequences to describe it. This process is called hyperparameterization of the learning space. In this way, a learning method can be represented as four infinite sequences, or further, the infinite-dimensional sequences can be finitely truncated and approximated as four finite sequences. After parameterization, a learning method can be described as four finite parameter sequences.

Learning Methodology

With the above preparation, we define learning methodology as a mapping from task space to learning space (denoted as LM). More specifically, given a task T, LM(T) is a value in the learning space, described by a four-tuple corresponding to the parameterized representation of data generation methods, hypothesis space/machine architecture, loss metrics, and optimization algorithms. This is learning methodology. Learning methodology is essentially a mapping on function space and a rule for assigning parameters. Clearly, SLeM is a function approximation problem on function space.

The problem-solving process based on SLeM is illustrated in Figure 7.

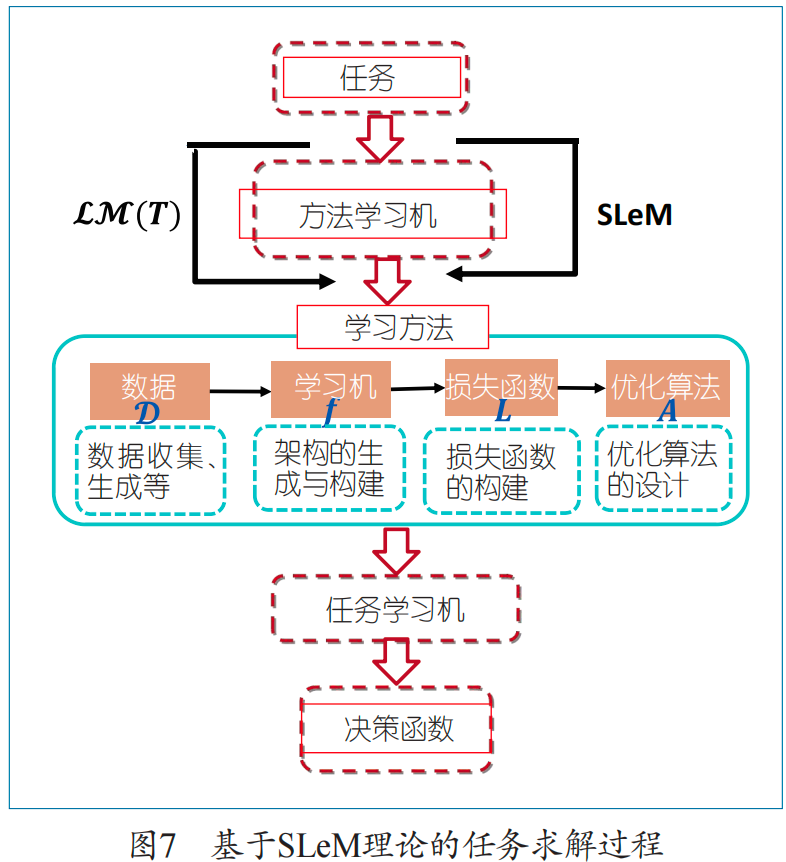
Unlike the traditional machine learning process (given data, machine architecture, selecting an optimization algorithm to solve, obtaining a decision function), solving problems based on SLeM adds a step of methodology learning before traditional machine learning, and then executes the machine learning task according to the method designed from methodology learning. Therefore, it is a two-stage task-solving process that starts from the task, generates methods, and then executes tasks.

Computational Models of SLeM Based on Metadata

SLeM can be described as a standard machine learning problem on function space. However, this model only has theoretical significance. However, if we make some assumptions, we can turn such a machine learning model into a computable model. For example, if we assume that the quality of the learning methodology can be judged by a set of metadata (similar to measuring a teacher’s teaching performance by students’ exam scores, where metadata can be likened to a set of standard exam questions), then the SLeM model can be transformed into an operable two-stage optimization model that can be conveniently processed by computers. Furthermore, if we replace the metadata used to measure the quality of the methodology with meta-knowledge, i.e., judging methodology based on rules, we can obtain another type of two-layer optimization SLeM model, which is the meta-knowledge-based SLeM model. In summary, different SLeM computational models can be obtained based on different evaluation criteria for methodologies.

Comparison of SLeM Framework with Other Frameworks

The general problem-solving based on SLeM starts from the task, generates methods according to the task, and then completes the task. The entire solving process can be divided into two stages: “method learning” and “task learning”. Clearly, this is different from current machine learning; the generalization goals of the two are different, and the inputs, structures, and models are also different. The SLeM framework is also very different from meta-learning, which includes many evolutionary processes, but overall, it is heuristic and lacks a clear mathematical model.

Transfer Learning Theory

We first applied SLeM theory to solve the metric problem of transfer learning. We know that the goal of artificial intelligence is transfer learning, but current transfer learning has not had good theoretical support. Using SLeM theory, we can prove that whether knowledge learned from completing some tasks can be transferred depends on three basic elements. First, whether we have previously encountered this task, i.e., the relevance of the task. Second, the spatial complexity of the task machine and the learning machine. Third, the consistency of the metadata used to measure methodology and training data. The discovery of these three elements indicates the possibility of constructing transfer learning theory.

Automation of Machine Learning

Next, we demonstrate how to solve the problem of machine learning automation using SLeM theory. First, we need to consider data automation: parameterizing by assigning weights to each data point, using the SLeM model to automatically select suitable data for network training from large amounts of data (i.e., self-selection of data). We proposed a methodology learning machine called Class-aware Meta-Weight-Net. Application demonstration shows that the learning effect based on data selected through SLeM is far superior to that of not selecting, manually selecting, or randomly selecting datasets, and the method based on SLeM is applicable to unbalanced and high-noise datasets. This method won the championship in the Guangdong-Hong Kong-Macao Greater Bay Area Algorithm Competition (2022). SLeM has also been used for label self-correction, i.e., automatically correcting mislabelled data to solve the label correction problem arising from semi-supervised learning. Regarding network automation, we have attempted to automatically embed transformation issues in deep learning, achieving very good results. Utilizing SLeM theory can also facilitate metric automation learning, in other words, adaptively setting loss metrics related to tasks. We proposed a methodology learning network called Meta Loss Adjuster, achieving good learning results. Finally, we applied SLeM to algorithm automation, specifically learning how to automatically set the learning rate of the BP algorithm. To this end, we designed a methodology network called Meta-LR-Schedule-Net. Testing shows that coupling Meta-LR-Schedule-Net improves the generalization performance of deep learning by about 4%.

In summary, by constructing a SLeM methodology machine, we can learn hyperparameter assignments with clear physical meanings for different tasks and achieve automation tasks in machine learning. The author’s team has made all research results publicly available on the open-source platform, see https://github.com/xjtushujun/Auto-6ML.

The current application of artificial intelligence is still characterized by “machine learning with prior assumptions” and manual processes; the next step in development will inevitably pursue “achieving automation in machine learning”, which is a fundamental issue in the development of machine learning. Achieving automation in machine learning requires the design and regulation of elements such as data, networks, losses, algorithms, and tasks. Realizing this goal requires “mapping from tasks to methods”, i.e., learning of learning methodologies (SLeM); existing research/methods do not yet support the realization of this goal. The author’s team has proposed the mathematical framework, strict definitions, mathematical models, and general algorithms of SLeM, demonstrating how to solve the problem of machine learning automation using SLeM methods. SLeM provides a formalized, modeled, and scientific research framework and approach for machine learning automation. Existing applications indicate that SLeM is a powerful and effective tool. The key to applying SLeM lies in the hyperparameterization scheme of the learning space and the design of the methodology learning machine. Additionally, the selection of metadata sets is a key factor determining the effectiveness of SLeM. SLeM is rapidly developing, and we look forward to its continued deepening, broadening, and toolification.

(This article is based on the invited report at CNCC2022)

XU Zongben

Professor at the School of Mathematics and Statistics, Xi’an Jiaotong University. Academician of the Chinese Academy of Sciences. His main research directions are intelligent information processing, machine learning, and foundational theories of data modeling.

[email protected]

Liu Kebin

CCF professional member. Associate researcher at Tsinghua University. His main research directions are the Internet of Things and ubiquitous computing.

[email protected]

Zhu Zhui

CCF student member. PhD student at the Department of Automation, Tsinghua University. His main research directions are edge intelligence and the Internet of Things.

[email protected]

Recommended by CCF