This article, written by Professor Hu Zhanyi from the Institute of Automation, Chinese Academy of Sciences, provides a brief summary of the development of computer vision over the past 40 years, including: Marr’s computational theory of vision, active and purpose-driven vision, multi-view geometry and camera self-calibration, and learning-based vision. Based on this foundation, some prospects for the future development trends of computer vision are presented.
The article was published on the WeChat public account of the Machine Vision Research Group, which is affiliated with the National Key Laboratory of Pattern Recognition at the Institute of Automation, Chinese Academy of Sciences. The Deep Blue Academy has not made any modifications to the article.
What is Computer Vision?

The Four Main Stages of Computer Vision Development
1
Marr’s Computational Vision
1
Marr’s Computational Vision
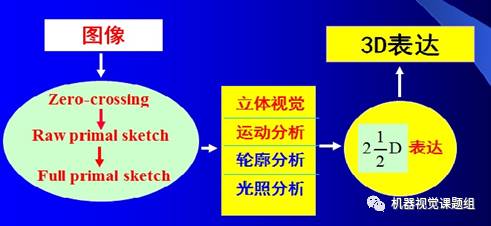
Computational Theory

Representation and Algorithms
2
Ephemeral Active and Purpose-Driven Vision
2
Ephemeral Active and Purpose-Driven Vision
3
Multi-View Geometry and Hierarchical 3D Reconstruction
3
Multi-View Geometry and Hierarchical 3D Reconstruction
Multi-View Geometry
Hierarchical 3D Reconstruction
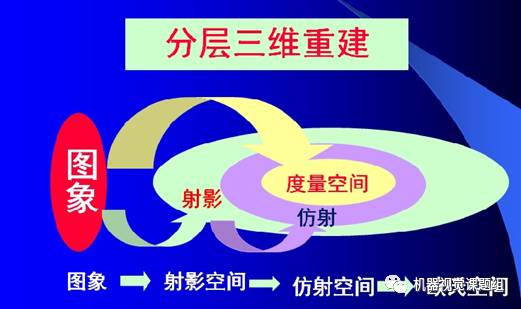
Camera Self-Calibration
4
Learning-Based Vision
4
Learning-Based Vision
Manifold Learning
Deep Learning
Several Development Trends in Computer Vision
Several Typical Theories of Object Representation
1
Marr’s Three-Dimensional Object Representation
1
Marr’s Three-Dimensional Object Representation
2
Two-Dimensional Image-Based Object Representation
2
Two-Dimensional Image-Based Object Representation
3
Inverse Generative Model Representation
3
Inverse Generative Model Representation
References
