Fundamentals of Neural Networks

(Click the public account above, you can quickly follow)

Source: Poll’s Notes

cnblogs.com/maybe2030/p/5597716.html

If you have good articles to submit, please click → here for details

Table of Contents

1. Neuron Model
2. Perceptron and Neural Networks
3. Backpropagation Algorithm
4. Common Neural Network Models
5. Deep Learning
6. References

Currently, deep learning (Deep Learning, abbreviated as DL) is flourishing in the field of algorithms. It is not only reflected in the internet and artificial intelligence but also brings significant changes to various fields in daily life. To learn deep learning, one must first be familiar with some basic concepts of neural networks (Neural Networks, abbreviated as NN). Of course, the neural networks mentioned here are not biological neural networks; it seems more reasonable to refer to them as artificial neural networks (Artificial Neural Networks, abbreviated as ANN). Neural networks were initially a type of algorithm or model in the field of artificial intelligence, and they have now evolved into a multidisciplinary field that has regained attention and respect with the progress of deep learning.

Why do we say “regain”? In fact, neural networks have been studied for a long time as an algorithmic model, but after making some progress, research on neural networks fell into a long period of low tide. Later, with Hinton’s advancements in deep learning, neural networks regained people’s attention. This article focuses on neural networks, summarizing some relevant foundational knowledge, and then introduces the concept of deep learning. If there are any mistakes in writing, please feel free to critique and correct.

1. Neuron Model

A neuron is the most basic structure in a neural network and can be regarded as the basic unit of a neural network. Its design inspiration comes entirely from the information transmission mechanism of biological neurons. Students who have studied biology know that neurons have two states: excitation and inhibition. Generally, most neurons are in an inhibitory state, but once a neuron receives stimulation that causes its potential to exceed a threshold, that neuron will be activated and enter an “excited” state, subsequently transmitting chemical substances (which are essentially information) to other neurons.

The diagram below shows the structure of a biological neuron:

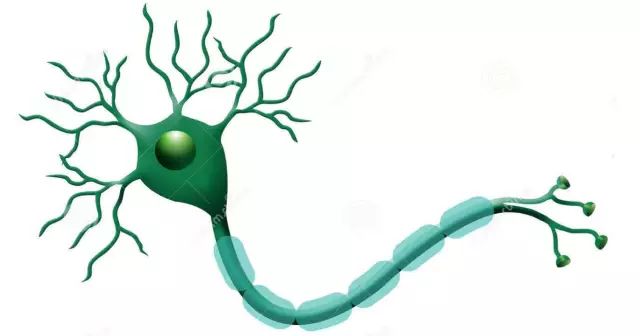
In 1943, McCulloch and Pitts represented the neuron structure shown above with a simple model, forming a type of artificial neuron model, which is commonly referred to as the “M-P neuron model,” as shown in the diagram below:

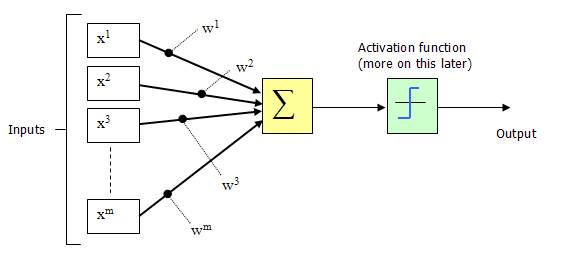
From the M-P neuron model shown above, we can see the output of the neuron:

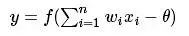
Fundamentals of Neural Networks

Where θ is the activation threshold of the neuron mentioned earlier, and the function f(⋅) is also known as the activation function. As shown in the diagram, the function f(⋅) can be represented by a step function, which activates when exceeding the threshold; otherwise, it inhibits. However, this is a bit too crude because the step function is not smooth, discontinuous, and not differentiable. Therefore, the more common method is to use the sigmoid function to represent the function f(⋅).

The expression and distribution diagram of the sigmoid function are shown below:

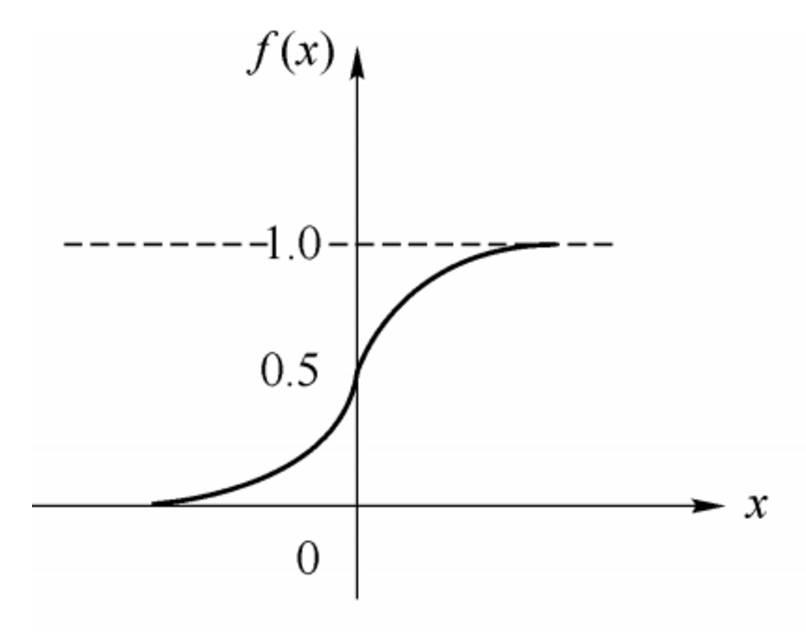
2. Perceptron and Neural Networks

A perceptron is a structure composed of two layers of neurons, where the input layer is used to receive external input signals, and the output layer (also known as the functional layer of the perceptron) consists of M-P neurons. The diagram below represents a perceptron structure with an input layer containing three neurons (denoted as x0, x1, x2):

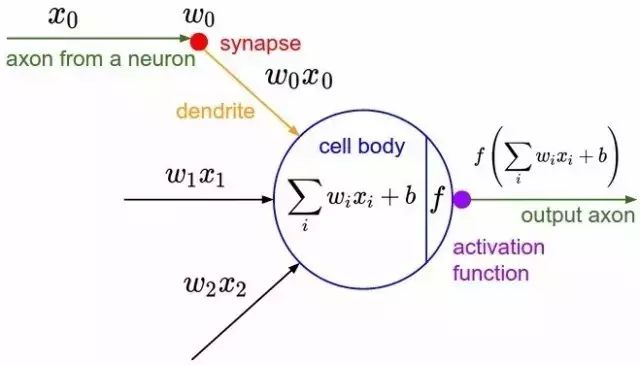
From the diagram, it is easy to understand that the perceptron model can be represented by the following formula:

y=f(wx+b)

Where w represents the weights connecting the input layer to the output layer of the perceptron, and b denotes the bias of the output layer. In fact, the perceptron is a discriminative linear classification model that can solve simple linear separable problems such as AND, OR, and NOT. The diagram of linear separable problems is shown below:

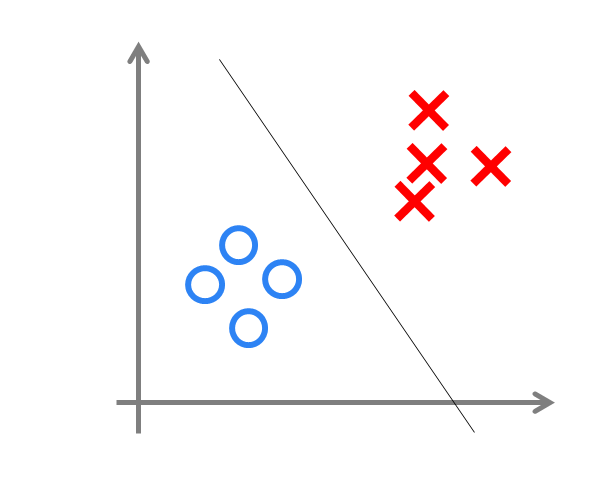However, since it only has one layer of functional neurons, its learning capability is very limited. It has been proven that a single-layer perceptron cannot solve the simplest non-linear separable problem—the XOR problem.

There is a historical background worth understanding regarding the perceptron and the XOR problem: perceptrons can only perform simple linear classification tasks. However, at that time, people were overly enthusiastic and did not recognize this fact. When the giant of artificial intelligence, Minsky, pointed this out, the situation changed. Minsky published a book titled “Perceptron” in 1969, which mathematically proved the weaknesses of perceptrons, especially their inability to solve simple classification tasks like XOR. Minsky believed that if the computational layer was increased to two layers, the computational load would be too large, and there would be no effective learning algorithm. Thus, he thought that researching deeper networks was of no value. Due to Minsky’s significant influence and the pessimistic attitude presented in his book, many scholars and laboratories abandoned research on neural networks, leading to a period known as the “AI winter.” It was nearly a decade before research on two-layer neural networks revived the field.

We know that many problems in our daily lives, in fact, most problems, are not linearly separable. So how do we handle non-linear separable problems? This leads us to the concept of “multi-layer.” Since a single-layer perceptron cannot solve non-linear problems, we use a multi-layer perceptron. The diagram below illustrates a two-layer perceptron solving the XOR problem:

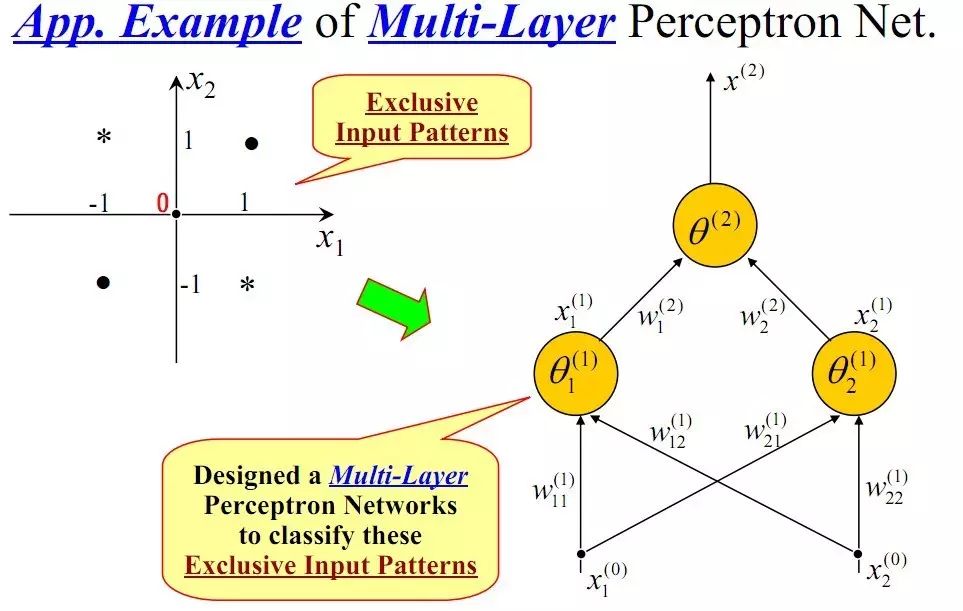
After constructing the network above, the final classification surface obtained through training is as follows:

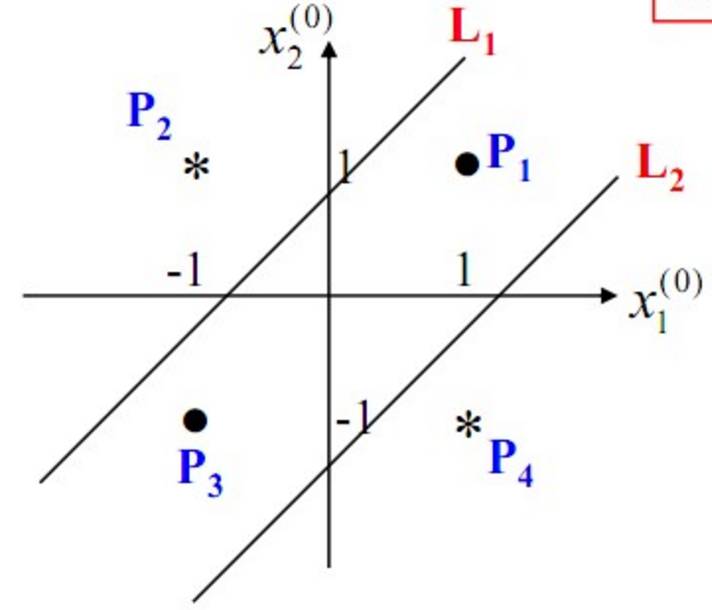
It can be seen that a multi-layer perceptron can effectively solve non-linear separable problems. We usually refer to such multi-layer structures as neural networks. However, just as Minsky previously worried, while multi-layer perceptrons can theoretically solve non-linear problems, the complexity of real-life problems goes far beyond the simplicity of the XOR problem. Therefore, we often need to construct multi-layer networks, and determining what learning algorithm to use for multi-layer neural networks poses a significant challenge. In the network structure with four hidden layers shown in the diagram below, there are at least 33 parameters (excluding the bias parameters). How should we determine these?

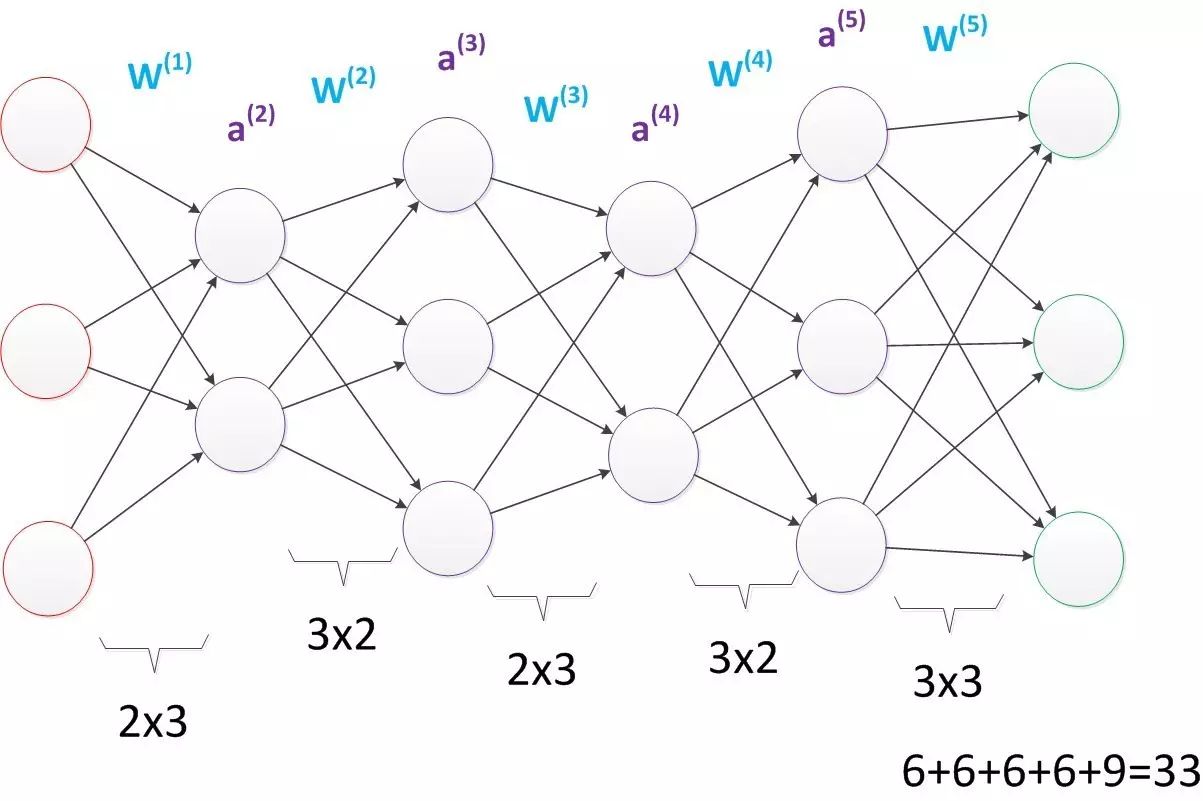
3. Backpropagation Algorithm

The so-called training or learning of neural networks mainly aims to obtain the parameters required for the neural network to solve specified problems through learning algorithms. These parameters include the connection weights between neurons in each layer and biases, etc. As the designers of the algorithm (we), we usually construct the network structure based on the actual problem, and the determination of parameters requires the neural network to iteratively find the optimal parameter set through training samples and learning algorithms.

When it comes to learning algorithms for neural networks, we must mention the most outstanding and successful representative—the Backpropagation (BP) algorithm. The BP learning algorithm is typically used in the most widely used multi-layer feedforward neural networks.

4. Common Neural Network Models

4.1 Boltzmann Machines and Restricted Boltzmann Machines

In neural networks, there is a class of models that define an “energy” for the network state; when the energy is minimized, the network reaches an ideal state, and the training of the network involves minimizing this energy function. The Boltzmann machine is an energy-based model, with neurons divided into two layers: the visible layer and the hidden layer. The visible layer represents the input and output of the data, while the hidden layer is understood as the intrinsic representation of the data. The neurons in a Boltzmann machine are all Boolean, meaning they can only take values of 0 or 1. The standard Boltzmann machine is fully connected, meaning that all neurons within each layer are interconnected, resulting in high computational complexity and making it difficult to solve practical problems. Therefore, we often use a special type of Boltzmann machine—the Restricted Boltzmann Machine (RBM), which has no connections within layers and connections between layers, and can be viewed as a bipartite graph. The diagram below illustrates the structure of Boltzmann machines and RBMs:

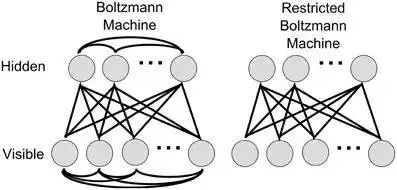
RBMs are often trained using Contrastive Divergence (CD).

4.2 RBF Networks

The Radial Basis Function (RBF) network is a type of single hidden layer feedforward neural network that uses radial basis functions as the activation functions of the hidden layer neurons, while the output layer is a linear combination of the outputs of the hidden layer neurons. The diagram below illustrates an RBF neural network:

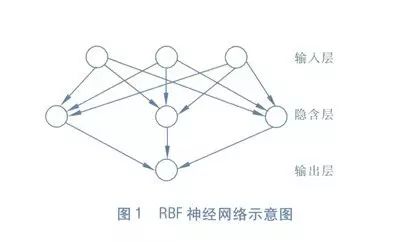
Training an RBF network typically involves two steps:

Determine the centers of the neurons, commonly through random sampling, clustering, etc.;
Determine the parameters of the neural network, with the commonly used algorithm being the BP algorithm.

4.3 ART Networks

The Adaptive Resonance Theory (ART) network is an important representative of competitive learning, consisting of a comparison layer, recognition layer, recognition layer threshold, and reset module. ART effectively alleviates the “stability-plasticity dilemma” in competitive learning, where plasticity refers to the network’s ability to learn new knowledge, while stability refers to the network’s ability to retain memory of old knowledge during the learning of new knowledge. This gives the ART network a significant advantage: it can perform incremental learning or online learning.

4.4 SOM Networks

The Self-Organizing Map (SOM) network is a type of competitive learning unsupervised neural network that can map high-dimensional input data to a lower-dimensional space (usually two-dimensional), while preserving the topological structure of the input data in the high-dimensional space, meaning that similar sample points in the high-dimensional space are mapped to adjacent neurons in the network output layer. The diagram below illustrates the structure of SOM networks:

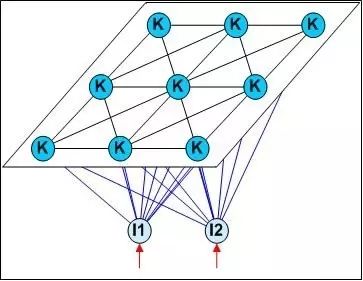
4.5 Structure-Adaptive Networks

As mentioned earlier, general neural networks typically specify the network structure beforehand, and the purpose of training is to determine suitable connection weights, thresholds, and other parameters using training samples. In contrast, structure-adaptive networks treat the network structure as one of the learning objectives and aim to find a network structure that best fits the characteristics of the data during the training process.

4.6 Recurrent Neural Networks and Elman Networks

Unlike feedforward neural networks, Recurrent Neural Networks (RNN) allow for cyclic structures within the network, enabling some neurons’ outputs to feedback as input signals. This structure and information feedback process mean that the network’s output state at time t not only depends on the input at time t but also on the network state at time t−1, allowing it to handle dynamic changes over time.

The Elman Network is one of the most commonly used recurrent neural networks, with the structure shown in the diagram below:

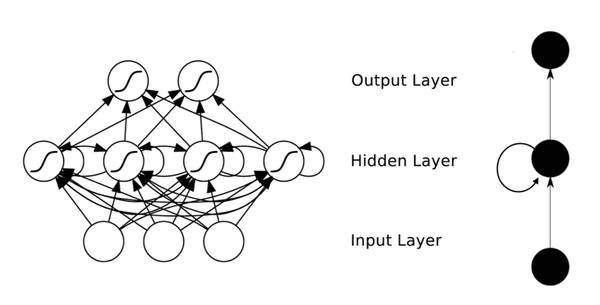
The typical training algorithm for RNNs employs an extended BP algorithm. It is worth noting that the result O(t+1) of the network at time (t+1) is the result of the current input and all historical influences, achieving the purpose of modeling time series. Therefore, in a sense, RNNs can be viewed as deep learning in the temporal dimension.

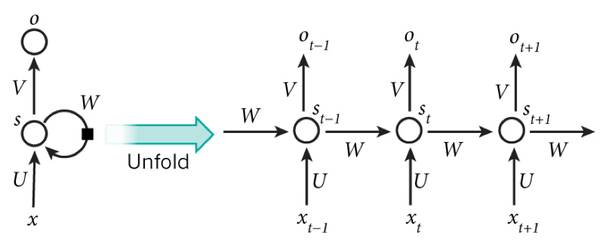
The result O(t+1) of the network at time (t+1) is influenced by both the current input and all historical factors, but this is not entirely accurate because “gradient vanishing” can also occur along the time axis. This means that for time t, the gradient it generates can disappear after propagating through several layers of history, failing to influence the distant past. Therefore, “all history” is merely an ideal case. In practice, such influence can only be maintained over a limited number of time steps. In other words, the error signals from later time steps often cannot return far enough into the past, like earlier time steps, to influence the network, making it difficult to learn long-distance influences.

To address the gradient vanishing issue along the time axis, the field of machine learning has developed Long Short-Term Memory units (LSTM), which implement memory functions over time through gate mechanisms and prevent gradient vanishing. In fact, in addition to learning historical information, RNNs and LSTMs can also be designed as bidirectional structures, namely bidirectional RNNs and bidirectional LSTMs, simultaneously utilizing historical and future information.

5. Deep Learning

Deep learning refers to deep neural network models, generally indicating neural network structures with three or more layers.

Theoretically, the more parameters a model has, the higher its complexity and “capacity,” meaning it can accomplish more complex learning tasks. Just like the insights provided by multi-layer perceptrons earlier, the number of layers in a neural network directly determines its ability to represent reality. However, under normal circumstances, training complex models is inefficient and prone to overfitting, making them less favored. Specifically, as the number of layers in a neural network increases, the optimization function is more likely to get stuck in local optima (i.e., overfitting, where it performs well on the training samples but poorly on the test set). Additionally, an important issue that cannot be ignored is that with the increase in the number of layers, the phenomenon of “gradient vanishing” (or gradient divergence) becomes more severe. We often use the sigmoid function as the activation function for hidden layer neurons; for a signal with an amplitude of 1, during backpropagation, the gradient diminishes to 0.25 for each layer passed. As the number of layers increases, the gradient exponentially decays, making it difficult for lower layers to receive effective training signals.

To solve the training issues of deep neural networks, an effective approach is to adopt unsupervised layer-wise training, where the basic idea is to train one layer of hidden nodes at a time, using the output of the previous layer as input and the output of the current layer as input to the next layer. This is referred to as “pre-training”; after pre-training is completed for all layers, the entire network undergoes “fine-tuning” training. For example, in Hinton’s Deep Belief Networks (DBN), each layer is an RBM, meaning the entire network can be viewed as a stack of several RBMs. During unsupervised training, the first layer is trained as an RBM model based on the training samples; then, the hidden nodes of the first layer are treated as input nodes for the second layer, and the second layer is pre-trained;… After pre-training is completed for all layers, the BP algorithm is used to train the entire network.

In fact, the “pre-training + fine-tuning” training method can be viewed as grouping a large number of parameters, finding locally optimal settings for each group, and then combining these locally optimal results for global optimization. This effectively utilizes the degrees of freedom provided by the model’s numerous parameters while saving training costs.

Another approach to reduce training costs is “weight sharing,” where a group of neurons share the same connection weights. This strategy plays a crucial role in Convolutional Neural Networks (CNN). The diagram below illustrates a CNN network:

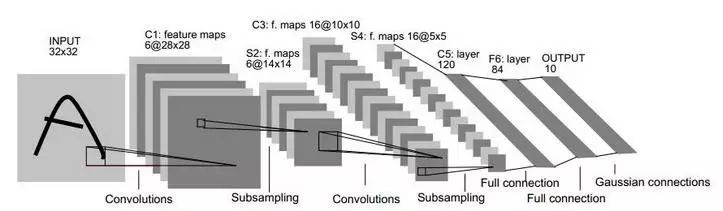
CNNs can be trained using the BP algorithm; however, during training, whether in convolutional layers or sampling layers, each group of neurons (i.e., each “plane” in the diagram above) uses the same connection weights, significantly reducing the number of parameters that need to be trained.