
This article introduces the ICML 2020 paper “Do RNN and LSTM have Long Memory?“. The authors of the paper are from Huawei Noah’s Ark Lab and the University of Hong Kong..

Paper link: https://arxiv.org/abs/2006.03860
To overcome the difficulties of Recurrent Neural Networks (RNNs) in learning long-term dependencies, Long Short-Term Memory (LSTM) networks were proposed in 1997 and have since made significant progress in applications. Many papers have confirmed the practicality of LSTMs and attempted to analyze their properties. However, the question “Do RNNs and LSTMs have long-term memory?” remains unanswered. This paper answers the question from a statistical perspective, proving that RNNs and LSTMs do not possess long-term memory in the statistical sense when making time series predictions. The existing definitions of long-term memory in statistics do not apply to neural networks, so we propose a new definition applicable to neural networks and use this new definition to analyze the theoretical properties of RNNs and LSTMs again. To validate our theory, we made minimal modifications to RNNs and LSTMs, converting them into long-term memory neural networks, and verified their superiority on datasets with long-term memory properties.
Although the term long-term memory is often mentioned in the application of LSTMs in deep learning, there is no strict definition. In the field of statistics, a strict definition of long-term memory has existed for a long time. For a second-order stationary one-dimensional time series, let its autocovariance function be defined as…
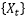 Then if…
Then if…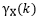 is not summable, then…
is not summable, then…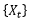 has long-term memory; if…
has long-term memory; if…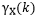 is summable, then…
is summable, then…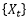 has short-term memory. Besides the autocovariance function, it can also be equivalently defined using the spectral density function. More rigorous statements can be found in the definition shown in the figure below.
A common time series model that meets the definition of long-term memory is the fractionally integrated process. In time series analysis, the shorthand for time series generally uses the backshift operator…
has short-term memory. Besides the autocovariance function, it can also be equivalently defined using the spectral density function. More rigorous statements can be found in the definition shown in the figure below.
A common time series model that meets the definition of long-term memory is the fractionally integrated process. In time series analysis, the shorthand for time series generally uses the backshift operator…
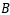 When…
When…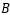 is applied to a random variable in the time series, it obtains the random variable at the previous moment, that is…
is applied to a random variable in the time series, it obtains the random variable at the previous moment, that is…
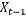 Backshift operator…
Backshift operator…
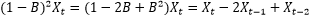 operations are very similar to operations with an algebraic variable, for example…
operations are very similar to operations with an algebraic variable, for example…
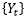 Using the backshift operator, a fractionally integrated process…
Using the backshift operator, a fractionally integrated process…
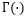 is the Gamma function,
is the Gamma function, 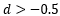 is the memory parameter of the fractionally integrated model. Generally, it is chosen as an Autoregressive Moving Average model (ARMA), at which point…
is the memory parameter of the fractionally integrated model. Generally, it is chosen as an Autoregressive Moving Average model (ARMA), at which point…
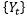 follows the Autoregressive Fractionally-Integrated Moving-Average model (ARFIMA). The ARMA part in an ARFIMA model is responsible for modeling short-term memory patterns, while the fractionally integrated parameter…
follows the Autoregressive Fractionally-Integrated Moving-Average model (ARFIMA). The ARMA part in an ARFIMA model is responsible for modeling short-term memory patterns, while the fractionally integrated parameter…
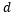 is responsible for modeling long-term memory patterns.
There is no unique definition of long-term memory for multidimensional time series. We choose a simple and direct way to define long-term memory for multidimensional time series, which is to check whether each dimension of the time series has long-term memory, ignoring the long-term correlations between different dimensions. Each dimension…
is responsible for modeling long-term memory patterns.
There is no unique definition of long-term memory for multidimensional time series. We choose a simple and direct way to define long-term memory for multidimensional time series, which is to check whether each dimension of the time series has long-term memory, ignoring the long-term correlations between different dimensions. Each dimension…
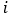 has a memory parameter…
has a memory parameter…
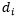 to model that dimension. The shorthand for the multidimensional model can be seen in equation (4).
The ARFIMA model is one of the important inspirations for this paper. Some of its important properties include:
to model that dimension. The shorthand for the multidimensional model can be seen in equation (4).
The ARFIMA model is one of the important inspirations for this paper. Some of its important properties include:
-
When the value is between -0.5 and 0.5, the model is stationary, and when it is greater than 0.5, the model is non-stationary;
-
For stationary models, if the value is less than 0, the model has short-term memory, while if it is greater than 0, the model has long-term memory, and the larger the value, the longer the memory effect;
-
The coefficients in equation (3) decay at a polynomial rate as the value increases, that is…
-
The autocovariance function decays at a polynomial rate.
The coefficients or autocovariance functions that decay at a polynomial rate are a significant feature distinguishing the ARFIMA model from short-term memory models. Models with short-term memory have coefficients or autocovariance functions that decay at an exponential rate, resulting in the rapid loss of past information. Combining with Definition 1, sequences with polynomial rate decay are non-summable when the exponent is less than -1, while sequences with exponential rate decay are always summable. Therefore, if the autocovariance function belongs to the former, the model has long-term memory; if it belongs to the latter, the model does not have long-term memory. This paper also uses the decay rate to prove the memory properties of RNNs and LSTMs.
When proving the decay rate of the autocovariance function of the model, we leveraged the property of geometric ergodicity to assist in the proof, with specific definitions shown in the figure below. A Markov chain with geometric ergodicity converges to a stationary distribution at an exponential rate after…
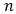 steps, meaning that the information of the Markov chain “currently in state” is lost at an exponential rate. Geometric ergodicity implies that the autocovariance function converges to 0 at an exponential rate, indicating that the stochastic process does not have long-term memory.
steps, meaning that the information of the Markov chain “currently in state” is lost at an exponential rate. Geometric ergodicity implies that the autocovariance function converges to 0 at an exponential rate, indicating that the stochastic process does not have long-term memory.
Memory Properties of Recurrent Networks
Assume that the input of a recurrent network is…
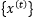 and the output is…
and the output is…
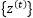 and the target sequence is…
and the target sequence is…
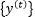 where…
where…
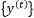 comes from the model…
comes from the model…
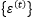 is independently and identically distributed white noise. The theoretical results of this section are established under the condition of time series prediction without exogenous variables, that is…
is independently and identically distributed white noise. The theoretical results of this section are established under the condition of time series prediction without exogenous variables, that is…
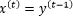 Considering a generic hidden state…
Considering a generic hidden state…
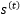 then a recurrent network can be expressed in the form of a Markov chain, see equation (7).
If the transition function…
then a recurrent network can be expressed in the form of a Markov chain, see equation (7).
If the transition function…
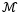 is linear, then equation (7) becomes a linear Markov chain.
is linear, then equation (7) becomes a linear Markov chain.
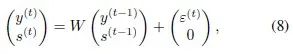 The Markov chain expressed in equation (7) actually includes RNNs or LSTMs.
For example, the most basic RNN, using the 2-norm loss function, has the feedforward computation as shown in equation (9).
The Markov chain expressed in equation (7) actually includes RNNs or LSTMs.
For example, the most basic RNN, using the 2-norm loss function, has the feedforward computation as shown in equation (9).
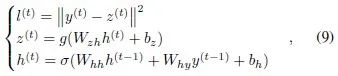 where…
where…
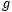 is the output function, and…
is the output function, and…
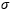 is the activation function. This RNN can be expressed in the form of the Markov chain in equation (7).
Similarly, for the basic LSTM network, the feedforward process is…
is the activation function. This RNN can be expressed in the form of the Markov chain in equation (7).
Similarly, for the basic LSTM network, the feedforward process is…
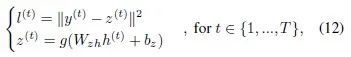 The calculations of the hidden layer unit involve the following gate operations…
The calculations of the hidden layer unit involve the following gate operations…
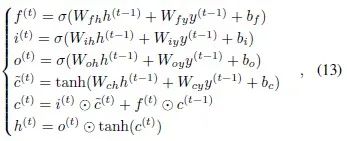 where…
where…
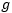 is the output function, and…
is the output function, and…
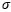 is the sigmoid activation function, while tanh is the hyperbolic tangent activation function. This LSTM process can also be written in the form of equation (7).
However, in LSTM, the hidden layer unit…
is the sigmoid activation function, while tanh is the hyperbolic tangent activation function. This LSTM process can also be written in the form of equation (7).
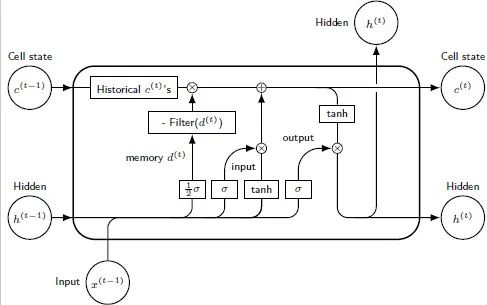
However, in LSTM, the hidden layer unit…
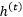 and the cell state…
and the cell state…
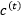 correspond to the generic hidden layer unit in (7).
The form of the transition function…
correspond to the generic hidden layer unit in (7).
The form of the transition function…
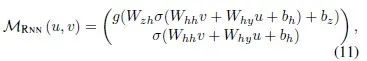 is more complex and will not be displayed here.
After adding two technical assumptions (see the figure, Assumption 1), we derived the two main conclusions of this paper. Theorem 1 provides a sufficient condition for recurrent networks (7) to have short-term memory, while Theorem 2 provides a necessary and sufficient condition for linear recurrent networks (8) to have short-term memory. These conditions are imposed on the transition function or transition matrix, so they hold for all recurrent network models that satisfy equation (7), including RNNs and LSTMs.
Theorem 1 is relatively abstract, as the conditions on the transition function cannot be intuitively converted into conditions on the weights and activation functions in the network. Thus, we further proposed Inference 1 and Inference 2. Inference 1 proves that as long as the output and activation functions of the RNN are continuous and bounded, the RNN has short-term memory, as shown in the figure below.
Inference 2 proposes sufficient conditions for LSTMs to have short-term memory. One is the condition on the output function; currently commonly used linear, ReLU, sigmoid, or tanh output functions all meet the requirements; the other requires that the output of the forget gate is strictly less than 1. Inference 2 reflects that the forget gate is key to the memory properties of LSTMs.
is more complex and will not be displayed here.
After adding two technical assumptions (see the figure, Assumption 1), we derived the two main conclusions of this paper. Theorem 1 provides a sufficient condition for recurrent networks (7) to have short-term memory, while Theorem 2 provides a necessary and sufficient condition for linear recurrent networks (8) to have short-term memory. These conditions are imposed on the transition function or transition matrix, so they hold for all recurrent network models that satisfy equation (7), including RNNs and LSTMs.
Theorem 1 is relatively abstract, as the conditions on the transition function cannot be intuitively converted into conditions on the weights and activation functions in the network. Thus, we further proposed Inference 1 and Inference 2. Inference 1 proves that as long as the output and activation functions of the RNN are continuous and bounded, the RNN has short-term memory, as shown in the figure below.
Inference 2 proposes sufficient conditions for LSTMs to have short-term memory. One is the condition on the output function; currently commonly used linear, ReLU, sigmoid, or tanh output functions all meet the requirements; the other requires that the output of the forget gate is strictly less than 1. Inference 2 reflects that the forget gate is key to the memory properties of LSTMs.
 The above theoretical results are established under the premise of no exogenous variables, while neural networks can perform operations with external variables in specific applications. If external variables inherently possess long-term memory properties, they will interfere with our analysis of the memory properties of neural networks, so existing statistical definitions of long-term memory cannot be used when external variables are present. To fill this gap, we propose a new definition of long-term memory applicable to neural networks. Assume that the neural network can be written (or approximated) in the following form…
The above theoretical results are established under the premise of no exogenous variables, while neural networks can perform operations with external variables in specific applications. If external variables inherently possess long-term memory properties, they will interfere with our analysis of the memory properties of neural networks, so existing statistical definitions of long-term memory cannot be used when external variables are present. To fill this gap, we propose a new definition of long-term memory applicable to neural networks. Assume that the neural network can be written (or approximated) in the following form…
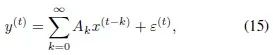 Then if the coefficient matrix has a dimension that decays at a polynomial rate, the network is considered to have long-term memory. Specific statements can be found in Definition 3.
Then if the coefficient matrix has a dimension that decays at a polynomial rate, the network is considered to have long-term memory. Specific statements can be found in Definition 3.
Long-Term Memory Recurrent Networks and Their Properties
Based on the theoretical results above, we aim to make minimal modifications to RNNs and LSTMs to enable them to model long-range dependencies. Similar to the structure in the ARFIMA model, we added a long-term memory filter at different positions in RNNs and LSTMs, resulting in Memory-augmented RNN (MRNN) and Memory-augmented LSTM (MLSTM) models.
The specific form of the long-term memory filter is…
The diagram of the MRNN network structure is…
where the long-term memory hidden layer unit…
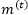 operates alongside the ordinary hidden layer unit…
operates alongside the ordinary hidden layer unit…
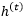 which is responsible for capturing information about long-term memory, while…
which is responsible for capturing information about long-term memory, while…
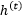 is responsible for modeling short-term information. The specific calculations are as follows…
The overall forward propagation process of MRNN can be expressed as…
To analyze the theoretical properties, we need to simplify the model. We refer to the fixed model as MRNNF, where the memory parameter…
is responsible for modeling short-term information. The specific calculations are as follows…
The overall forward propagation process of MRNN can be expressed as…
To analyze the theoretical properties, we need to simplify the model. We refer to the fixed model as MRNNF, where the memory parameter…
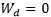 is constant over time. For the MRNNF model, we analyzed and obtained the following properties, namely that MRNNF satisfies Definition 3 and possesses long-term memory, while RNNs still do not possess long-term memory.
For the modifications to LSTM, we added the long-term memory filter to the cell state, as the original cell state of LSTM follows a dynamic coefficient AR(1) model…
is constant over time. For the MRNNF model, we analyzed and obtained the following properties, namely that MRNNF satisfies Definition 3 and possesses long-term memory, while RNNs still do not possess long-term memory.
For the modifications to LSTM, we added the long-term memory filter to the cell state, as the original cell state of LSTM follows a dynamic coefficient AR(1) model…
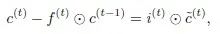 Therefore, we naturally added the state update here with the long-term memory filter, resulting in…
The diagram of the MSLTM network structure is…
The forward propagation process is…
Directly analyzing whether MLSTM satisfies Definition 3 is still challenging, so we performed a similar simplification to MRNNF, assuming that all gates do not change over time. Then, LSTMs with gates that do not change over time do not possess long-term memory, while MLSTMs with gates that do not change over time (referred to as MLSTMF) possess long-term memory. Note that this does not lead to the conclusion that LSTMs do not have long-term memory; it only indirectly suggests that the gate operations in LSTMs play an important role in their memory properties.
Therefore, we naturally added the state update here with the long-term memory filter, resulting in…
The diagram of the MSLTM network structure is…
The forward propagation process is…
Directly analyzing whether MLSTM satisfies Definition 3 is still challenging, so we performed a similar simplification to MRNNF, assuming that all gates do not change over time. Then, LSTMs with gates that do not change over time do not possess long-term memory, while MLSTMs with gates that do not change over time (referred to as MLSTMF) possess long-term memory. Note that this does not lead to the conclusion that LSTMs do not have long-term memory; it only indirectly suggests that the gate operations in LSTMs play an important role in their memory properties.
We conducted three experiments: first, to validate the advantages of the newly proposed models on datasets with long-term memory properties; second, to verify that the newly proposed models do not degrade performance on datasets with only short-term memory properties; and third, to explore the impact of the long-term memory filter length…
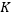 on model performance.
We first selected four datasets with long-term memory properties for time series prediction tasks: sequences generated by the ARFIMA model, returns from the Dow Jones index, subway passenger flow data from Minneapolis, and tree ring width data. The long-term memory properties of these datasets can be judged by plotting the sample autocorrelation function. For example, the autocorrelation function in the figure below shows a long trend, which is significantly different from white noise sequences, intuitively indicating that the data has long-term memory.
We compared eight models:
1. Original RNN, lookback = 1;
2. Dual-track RNN (similar to MRNN), but the filter part is unrestricted, with…
on model performance.
We first selected four datasets with long-term memory properties for time series prediction tasks: sequences generated by the ARFIMA model, returns from the Dow Jones index, subway passenger flow data from Minneapolis, and tree ring width data. The long-term memory properties of these datasets can be judged by plotting the sample autocorrelation function. For example, the autocorrelation function in the figure below shows a long trend, which is significantly different from white noise sequences, intuitively indicating that the data has long-term memory.
We compared eight models:
1. Original RNN, lookback = 1;
2. Dual-track RNN (similar to MRNN), but the filter part is unrestricted, with…
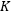 free weights;
3. Recurrent weighted average network (RWA);
4. MRNNF, where the memory parameter…
free weights;
3. Recurrent weighted average network (RWA);
4. MRNNF, where the memory parameter…
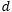 is constant over time;
5. MRNN, where the memory parameter…
is constant over time;
5. MRNN, where the memory parameter…
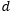 changes over time;
7. MLSTMF, where the memory parameter…
changes over time;
7. MLSTMF, where the memory parameter…
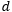 is constant over time;
8. MLSTM, where the memory parameter…
is constant over time;
8. MLSTM, where the memory parameter…
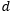 changes over time.
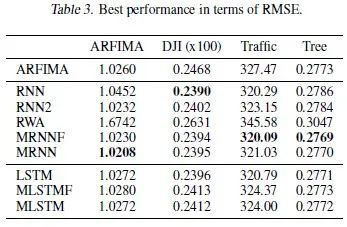
Since the training of these networks is a non-convex problem, initializing the models with different seeds will lead to different learned models. Therefore, we used 100 different seeds and reported the mean, standard deviation, and minimum of the error metrics for the time series prediction tasks. The mean and standard deviation of the errors are shown in Table 2, and the minimum values are shown in Table 3.
We plotted the performance of the 100 models learned from the 100 random seeds using a boxplot, as shown in Figure 4. Using a two-sample…
changes over time.
Since the training of these networks is a non-convex problem, initializing the models with different seeds will lead to different learned models. Therefore, we used 100 different seeds and reported the mean, standard deviation, and minimum of the error metrics for the time series prediction tasks. The mean and standard deviation of the errors are shown in Table 2, and the minimum values are shown in Table 3.
We plotted the performance of the 100 models learned from the 100 random seeds using a boxplot, as shown in Figure 4. Using a two-sample…
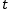 -test to compare the performance of MRNN and RNN/LSTM, the conclusion shows that the advantage of MRNN is significant.
Additionally, we also tested the application of our proposed long-term memory module in multilayer neural networks on the Spanish paper review dataset. To improve efficiency, we fixed the memory parameter…
-test to compare the performance of MRNN and RNN/LSTM, the conclusion shows that the advantage of MRNN is significant.
Additionally, we also tested the application of our proposed long-term memory module in multilayer neural networks on the Spanish paper review dataset. To improve efficiency, we fixed the memory parameter…
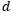 to be constant over time, set the filter length…
to be constant over time, set the filter length…
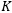 to 50, and only used the filter structure in the first layer. The second layer of the network was uniformly set to LSTM units, and the comparison results are as follows. Although MLSTM and MLSTMF did not show significant advantages on the time series prediction datasets, their advantages were very clear on this natural language processing classification task. Using a two-sample…
to 50, and only used the filter structure in the first layer. The second layer of the network was uniformly set to LSTM units, and the comparison results are as follows. Although MLSTM and MLSTMF did not show significant advantages on the time series prediction datasets, their advantages were very clear on this natural language processing classification task. Using a two-sample…
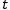 -test comparing the accuracy of MLSTMF and RNN/LSTM, the p-values were all less than 0.05.
In the second experiment, we generated data using RNN and used eight models for prediction, with the results shown in the figure below. Except for a slight increase in variance for the new model, there was no significant disadvantage. This indicates that our new model is also applicable to datasets with mixed long-term and short-term memory.
In the third experiment, we explored the impact of hyperparameters…
-test comparing the accuracy of MLSTMF and RNN/LSTM, the p-values were all less than 0.05.
In the second experiment, we generated data using RNN and used eight models for prediction, with the results shown in the figure below. Except for a slight increase in variance for the new model, there was no significant disadvantage. This indicates that our new model is also applicable to datasets with mixed long-term and short-term memory.
In the third experiment, we explored the impact of hyperparameters…
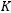 on model performance. The experiment selected…
on model performance. The experiment selected…
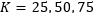 and 100 for comparison in four scenarios. The conclusion is that MRNN performs best when…
and 100 for comparison in four scenarios. The conclusion is that MRNN performs best when…
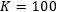 while MLSTM performs best when…
while MLSTM performs best when…
 We speculate that this may be due to the larger size of the MLSTM model, making it more difficult to train.
We speculate that this may be due to the larger size of the MLSTM model, making it more difficult to train.
This paper first proves that RNNs and LSTMs do not have long-term memory from the perspective of time series. By using the filter structure in the fractionally integrated process, we made corresponding modifications to RNNs and LSTMs, enabling them to handle data with long-range dependencies. In time series prediction tasks, MRNN and MRNNF demonstrated advantages across various datasets, while MLSTM and MLSTMF performed comparably to the original LSTM and were influenced by the filter length…
In future work, we can continue to explore whether similar filters can bring similar advantages to other recurrent or feedforward networks. Additionally, compared to other models, the computational overhead of dynamic MRNN and MLSTM is relatively large, and future research can focus on further simplifying the models and exploring faster optimization methods. Finally, according to Definition 3, we can also attempt many other information decay patterns to model long-term memory sequences, for example, by directly allowing the weights of the filters…
AI Technology Review hopes to recruit a technology editor/reporter.
Office Location: Beijing
Position: Focused on tracking academic hotspots and conducting interviews
Job Responsibilities:
1. Pay attention to hot events in the academic field and report them in a timely manner;
2. Interview scholars or researchers in the field of artificial intelligence;
3. Attend various artificial intelligence academic conferences and report on the content of the conferences.
Requirements:
1. Passionate about academic research in artificial intelligence and good at interacting with scholars or engineering personnel;
2. Having a certain background in science and engineering, with a better understanding of artificial intelligence technology;
3. Strong English skills (the job involves a lot of English materials);
4. Strong learning ability, with a certain understanding of cutting-edge artificial intelligence technologies, and able to gradually form one’s own opinions.
If interested, please send your resume to: [email protected]
Click “Read the original text” to go directly to the “ICML Communication Group” for more conference information.


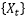 Then if…
Then if…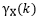 is not summable, then…
is not summable, then…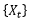 has long-term memory; if…
has long-term memory; if…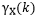 is summable, then…
is summable, then…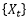 has short-term memory. Besides the autocovariance function, it can also be equivalently defined using the spectral density function. More rigorous statements can be found in the definition shown in the figure below.
has short-term memory. Besides the autocovariance function, it can also be equivalently defined using the spectral density function. More rigorous statements can be found in the definition shown in the figure below.
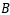 When…
When…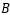 is applied to a random variable in the time series, it obtains the random variable at the previous moment, that is…
is applied to a random variable in the time series, it obtains the random variable at the previous moment, that is…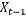 Backshift operator…
Backshift operator…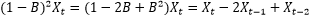 operations are very similar to operations with an algebraic variable, for example…
operations are very similar to operations with an algebraic variable, for example…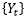 Using the backshift operator, a fractionally integrated process…
Using the backshift operator, a fractionally integrated process…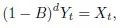
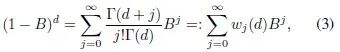
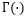 is the Gamma function,
is the Gamma function, 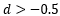 is the memory parameter of the fractionally integrated model. Generally, it is chosen as an Autoregressive Moving Average model (ARMA), at which point…
is the memory parameter of the fractionally integrated model. Generally, it is chosen as an Autoregressive Moving Average model (ARMA), at which point…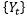 follows the Autoregressive Fractionally-Integrated Moving-Average model (ARFIMA). The ARMA part in an ARFIMA model is responsible for modeling short-term memory patterns, while the fractionally integrated parameter…
follows the Autoregressive Fractionally-Integrated Moving-Average model (ARFIMA). The ARMA part in an ARFIMA model is responsible for modeling short-term memory patterns, while the fractionally integrated parameter…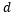 is responsible for modeling long-term memory patterns.
is responsible for modeling long-term memory patterns.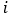 has a memory parameter…
has a memory parameter…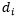 to model that dimension. The shorthand for the multidimensional model can be seen in equation (4).
to model that dimension. The shorthand for the multidimensional model can be seen in equation (4).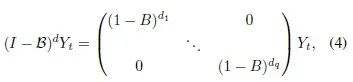
 steps, meaning that the information of the Markov chain “currently in state” is lost at an exponential rate. Geometric ergodicity implies that the autocovariance function converges to 0 at an exponential rate, indicating that the stochastic process does not have long-term memory.
steps, meaning that the information of the Markov chain “currently in state” is lost at an exponential rate. Geometric ergodicity implies that the autocovariance function converges to 0 at an exponential rate, indicating that the stochastic process does not have long-term memory.
 and the output is…
and the output is…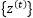 and the target sequence is…
and the target sequence is…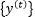 where…
where…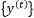 comes from the model…
comes from the model…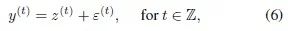
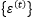 is independently and identically distributed white noise. The theoretical results of this section are established under the condition of time series prediction without exogenous variables, that is…
is independently and identically distributed white noise. The theoretical results of this section are established under the condition of time series prediction without exogenous variables, that is…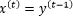 Considering a generic hidden state…
Considering a generic hidden state…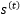 then a recurrent network can be expressed in the form of a Markov chain, see equation (7).
then a recurrent network can be expressed in the form of a Markov chain, see equation (7).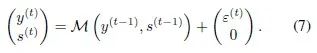
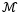 is linear, then equation (7) becomes a linear Markov chain.
is linear, then equation (7) becomes a linear Markov chain.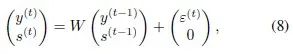 The Markov chain expressed in equation (7) actually includes RNNs or LSTMs.
The Markov chain expressed in equation (7) actually includes RNNs or LSTMs.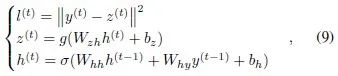 where…
where…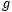 is the output function, and…
is the output function, and…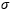 is the activation function. This RNN can be expressed in the form of the Markov chain in equation (7).
is the activation function. This RNN can be expressed in the form of the Markov chain in equation (7).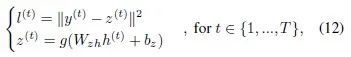 The calculations of the hidden layer unit involve the following gate operations…
The calculations of the hidden layer unit involve the following gate operations…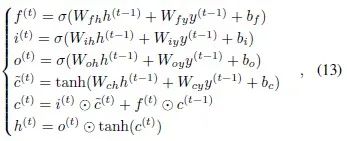 where…
where… is the output function, and…
is the output function, and…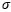 is the sigmoid activation function, while tanh is the hyperbolic tangent activation function. This LSTM process can also be written in the form of equation (7).
is the sigmoid activation function, while tanh is the hyperbolic tangent activation function. This LSTM process can also be written in the form of equation (7).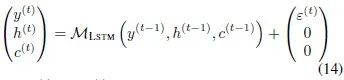
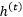 and the cell state…
and the cell state…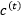 correspond to the generic hidden layer unit in (7).
correspond to the generic hidden layer unit in (7).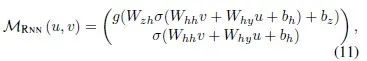 is more complex and will not be displayed here.
is more complex and will not be displayed here.


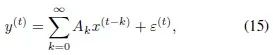 Then if the coefficient matrix has a dimension that decays at a polynomial rate, the network is considered to have long-term memory. Specific statements can be found in Definition 3.
Then if the coefficient matrix has a dimension that decays at a polynomial rate, the network is considered to have long-term memory. Specific statements can be found in Definition 3.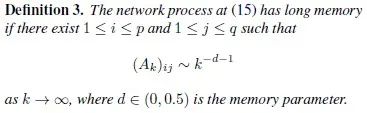
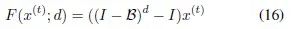
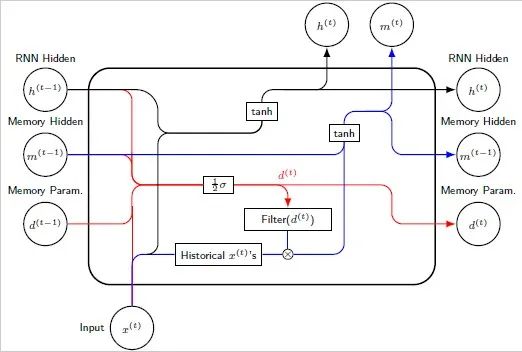
 operates alongside the ordinary hidden layer unit…
operates alongside the ordinary hidden layer unit… which is responsible for capturing information about long-term memory, while…
which is responsible for capturing information about long-term memory, while… is responsible for modeling short-term information. The specific calculations are as follows…
is responsible for modeling short-term information. The specific calculations are as follows…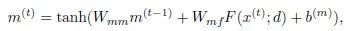
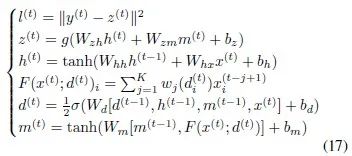
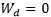 is constant over time. For the MRNNF model, we analyzed and obtained the following properties, namely that MRNNF satisfies Definition 3 and possesses long-term memory, while RNNs still do not possess long-term memory.
is constant over time. For the MRNNF model, we analyzed and obtained the following properties, namely that MRNNF satisfies Definition 3 and possesses long-term memory, while RNNs still do not possess long-term memory.
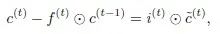 Therefore, we naturally added the state update here with the long-term memory filter, resulting in…
Therefore, we naturally added the state update here with the long-term memory filter, resulting in…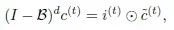
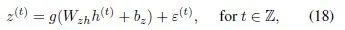
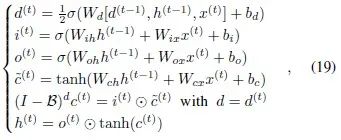
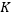 on model performance.
on model performance.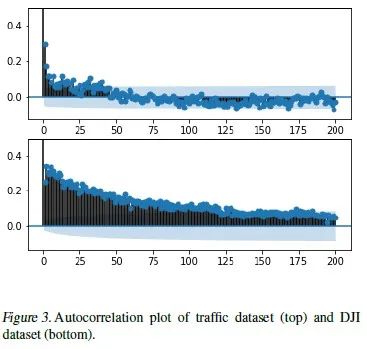
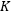 free weights;
free weights;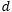 is constant over time;
is constant over time;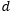 changes over time;
changes over time;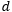 is constant over time;
is constant over time;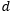 changes over time.
changes over time.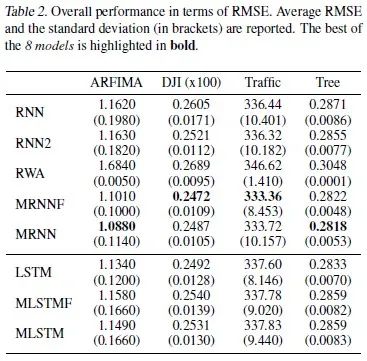
 -test to compare the performance of MRNN and RNN/LSTM, the conclusion shows that the advantage of MRNN is significant.
-test to compare the performance of MRNN and RNN/LSTM, the conclusion shows that the advantage of MRNN is significant.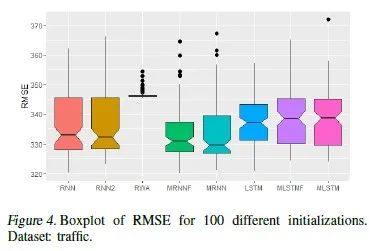
 to be constant over time, set the filter length…
to be constant over time, set the filter length…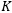 to 50, and only used the filter structure in the first layer. The second layer of the network was uniformly set to LSTM units, and the comparison results are as follows. Although MLSTM and MLSTMF did not show significant advantages on the time series prediction datasets, their advantages were very clear on this natural language processing classification task. Using a two-sample…
to 50, and only used the filter structure in the first layer. The second layer of the network was uniformly set to LSTM units, and the comparison results are as follows. Although MLSTM and MLSTMF did not show significant advantages on the time series prediction datasets, their advantages were very clear on this natural language processing classification task. Using a two-sample…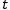 -test comparing the accuracy of MLSTMF and RNN/LSTM, the p-values were all less than 0.05.
-test comparing the accuracy of MLSTMF and RNN/LSTM, the p-values were all less than 0.05.
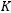 on model performance. The experiment selected…
on model performance. The experiment selected…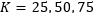 and 100 for comparison in four scenarios. The conclusion is that MRNN performs best when…
and 100 for comparison in four scenarios. The conclusion is that MRNN performs best when…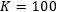 while MLSTM performs best when…
while MLSTM performs best when… We speculate that this may be due to the larger size of the MLSTM model, making it more difficult to train.
We speculate that this may be due to the larger size of the MLSTM model, making it more difficult to train.
