This article is adapted from: AI Academic Workshop

Title: Diffusion Mechanism in Residual Neural Network: Theory and Applications

Diffusion Mechanism in Residual Neural Networks: Theory and Applications

Authors: Tangjun Wang; Zehao Dou; Chenglong Bao; Zuoqiang Shi

Source code link: https://github.com/shwangtangjun/Diff-ResNet

Abstract

Diffusion is a fundamental internal mechanism that occurs in many physical processes, describing the interactions between different objects. In many learning tasks with limited training samples, diffusion connects labeled and unlabeled data points, serving as a key component for achieving high classification accuracy. Many existing deep learning methods directly impose fusion losses when training neural networks. Inspired by the convection-diffusion ordinary differential equations (ODEs), we propose a novel diffusion residual network (Diff-ResNet) that introduces diffusion internally into the architecture of neural networks. Under the assumption of structured data, we prove that the proposed diffusion block can increase the distance diameter ratio, enhancing the separability of inter-class points and reducing the distance between local intra-class points. Moreover, this property can be easily adopted by residual networks to construct separable hyperplanes. Extensive experiments on various datasets for synthetic binary classification, semi-supervised graph node classification, and few-shot image classification validate the effectiveness of the proposed method.

Keywords

• Diffusion, Residual Neural Networks, Ordinary Differential Equations, Semi-Supervised Learning, Few-Shot Learning.

I. Introduction

Residual networks (ResNet) and their variants, which include skip connections between different layers, are promising network architectures in deep learning. Compared to non-residual networks, ResNet significantly improves training stability and generalization accuracy. To understand the success of ResNet, a recent series of works have established its connection with ordinary differential equations (ODEs). Let x be a data point, the ODE model of ResNet is:

where f is a parameterized mapping. Clearly, the forward Euler discretization of (1) recovers the residual connections, inspiring the connection between ResNets and ODEs. Based on the above observations, many recent works have proposed from two perspectives: ODE-inspired neural networks and neural network-based ODEs. Specifically, the design methods of ODE-inspired neural networks can be divided into two directions. One design method for networks is to unfold the ODE system through different discretization schemes to construct an end-to-end mapping. Typical networks include PolyNet, FractalNet, and linear multi-step networks. The other method is to add some new blocks to the current network architecture by modifying the ODE model, such as noise injection, stochastic dynamic systems, and adding damping terms. Since ODEs have a strong mathematical foundation, the network architectures proposed in the above works have shown improved interpretability and performance. On the other hand, neural network-based ODE models parameterize the velocity through neural networks and find parameters using optimal control formulas. These methods enhance the expressiveness of traditional ODE methods and demonstrate promising results on various problems, including systems with irregular boundaries, PDEs in fluid dynamics, and high-dimensional differential equations. Therefore, the connection between ResNets and ODEs is worth exploring in depth.

The success of deep learning methods heavily relies on a large amount of training samples, but collecting training data requires significant labor and is sometimes impossible in many application domains due to privacy or security issues. To alleviate the dependence on training data, semi-supervised learning (SSL) and few-shot learning (FSL) have received great attention in recent years. Semi-supervised learning typically uses a large amount of unlabeled data along with labeled data to build better classifiers. Few-shot learning is a more recent paradigm closely related to semi-supervised learning, with the main difference being that the size of the support set (labeled points) is much smaller. A common feature of SSL and FSL is the utilization of unlabeled samples to address the issue of limited labeled sets. For reviews on SSL and FSL, see [18], [21]. In this work, we focus on deep learning-based approaches to solve the SSL problem. Generally, deep SSL methods can be divided into two categories: consistency regularization and entropy minimization. Consistency regularization requires that small perturbations to the input do not significantly change the output. The Π-Model and its more stable version Mean Teacher require that random network predictions across different passes are minimally disturbed. VAT replaces random perturbations with the ‘worst’ perturbation, which can maximally affect the output of the prediction function. Entropy minimization is closely related to self-training and encourages more confident predictions on unlabeled data. EntMin imposes low entropy requirements on the predictions of unlabeled samples. Pseudo-labels take unlabeled samples with high predicted confidence as labeled samples to train better classifiers. Additionally, some holistic methods attempt to unify currently effective SSL methods into one framework, such as MixMatch and FixMatch. Despite the existence of many deep SSL methods that achieve impressive results on various tasks, the internal mechanisms of consistency regularization or entropy minimization methods in SSL/FSL classification remain unclear.

To unveil this mystery in SSL and FSL, we propose an ODE-based deep neural network that is based on the connection between ODEs and ResNet. As shown in (1), the current ODE counterpart of ResNet is the convection equation. Each point controlled by (1) evolves independently. When a large number of training samples are available, this evolution process is acceptable, but performance significantly deteriorates when the number of supervised samples is reduced. Therefore, directly applying (1) to SSL/FSL may pose problems. To address this issue, we introduce a diffusion mechanism into (1), resulting in a convection-diffusion equation. After discretization, we obtain a diffusion-based residual neural network. The imposed diffusion is a key component in domains with limited training data, enforcing interaction between samples (including labeled and unlabeled ones). In fact, it is worth mentioning that convection and diffusion mechanisms always appear simultaneously in complex systems such as fluid dynamics, building physics, and semiconductors, which strongly inspires the integration of diffusion into deep ResNets.

Imposing interactions between samples is a classical idea that has appeared in many existing SSL methods, but the combination of convection and diffusion within network architectures has not been fully explored. Furthermore, most methods introduce diffusion by adding a Laplacian regularization term in the loss function, which is widely used in graph-based SSL. In this case, adjusting the weight of the Laplacian regularization term is not easy and is often sensitive to the task. Unlike the aforementioned methods, we explicitly add diffusion layers within ResNet. The proposed diffusion layer internally enforces interactions between samples and demonstrates higher effectiveness in SSL/FSL. More importantly, we provide a theoretical analysis of the diffusion ODE and show its advantages in the distance-diameter ratio between data samples, providing a solid foundation for the proposed method. In summary, our main contributions are as follows:

• We propose a convection-diffusion ODE model to address the SSL/FSL problem, leading to the addition of diffusion layers to ResNets after appropriate discretization. The proposed diffusion-based ResNet strengthens the relationship between labeled and unlabeled data points through well-designed network architectures, rather than imposing diffusion loss in the total loss. To our knowledge, this is the first attempt to integrate the diffusion mechanism internally into deep neural network architectures.
• Under the assumption of structured data, we prove that the diffusion mechanism can accelerate the classification process, allowing samples from different subclasses to be separated while samples from the same subclass are clustered together. Utilizing this property, we can theoretically construct a residual network that ensures the output features are linearly separable. This analysis provides a mathematical foundation for our method.
• Extensive experiments on various tasks and datasets validate our theoretical results and the advantages of the proposed Diff-ResNet.

The rest of this paper is organized as follows. Related work is presented in Section II. Section III introduces the formulation and details of our diffusion residual network, while Section IV provides a theoretical analysis of the diffusion mechanism. Experimental results on various tasks are reported in Section V. We conclude the paper in Section VI.

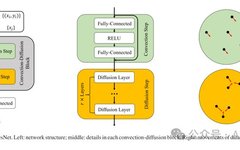
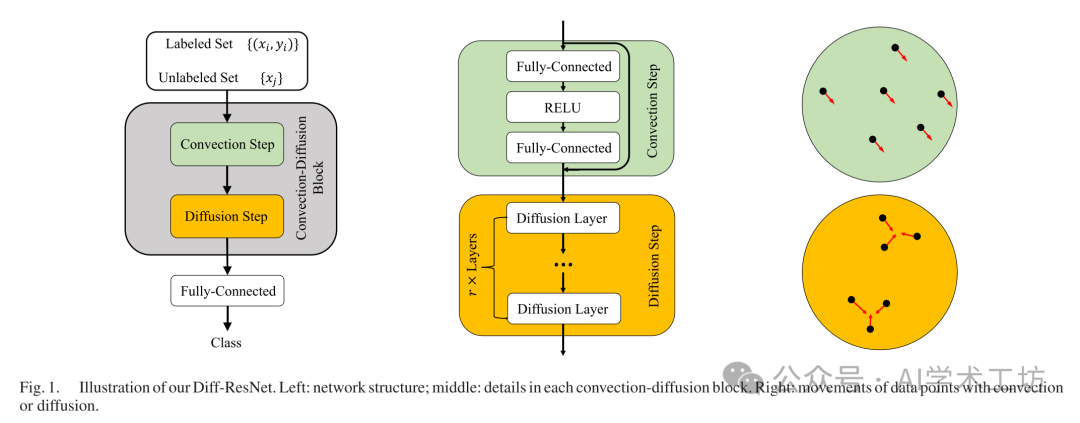
III. DIFFUSION RESIDUAL NETWORKS

In this section, we introduce the diffusion mechanism from the perspective of ODEs and propose Diff-ResNet based on the numerical scheme of diffusion ODEs.

A. The ODE Formulation

In ResNet [1], the feature map of a specific data point after the k-th residual block is defined as h_k(x). The residual connection means adding to h_k(x) through a skip identity link. If we group the convolutional layers, batch normalization layers, and other layers together and represent them as a function, each residual block can be written as:

where W_k is the parameters of the k-th block. From the perspective of ODEs, h_k(x) can be viewed as a velocity field, while h_k(0) and h_k(1) can be viewed as the starting and ending positions, respectively. By introducing a time step, we can absorb it into h_k, and ResNet can be regarded as the forward Euler discretization of the following ODE model that describes the evolution of x:

Time forms a continuous analogy to layer indices, with each layer corresponding to an iteration of evolution. This ODE only contains convection terms, with each point moving independently and without collisions. To enhance interactions between data points, especially among unlabeled samples, we introduce an additional diffusion term in (3) to obtain the following convection-diffusion ODE system:

for all x, where N is the number of points, λ is a parameter controlling the diffusion strength, and W is the weight between h_k(0) and h_k(1). By designing a weight matrix to describe the similarity between points, we can expect similar points to be pulled closer, while different points are pushed apart. In this paper, the convection term is set to a simple 2-layer network with width d, that is:

Here, W_1, W_2, b_1, b_2 are the parameters, and ReLU is the activation function. t is the set of network weights at time. In the next section, we will derive a practical algorithm based on the new ODE (4).

B. Algorithm

We discretize the convection-diffusion (4) using the classical Lie-Trotter splitting scheme [75]. After absorbing the time step into h_k and h_{k+1}, we obtain:

The convection step (6) is almost identical to the residual block (2), just with a different time step, which is not a fundamental distinction in implementation. The added diffusion step (7) can be viewed as a stabilization of the convection step (6). If the weight matrix is pre-computed, the diffusion step is non-parametric, and thus the proposed diffusion term can be easily integrated into any existing network or algorithm in a plug-and-play manner. To construct the weight matrix, we use a Gaussian kernel to measure the similarity between data points. σ is the parameter to adjust the weight distribution. Next, we introduce two operators, Sparse and Normalize, along with a hyperparameter ntop to obtain a sparse and balanced weight matrix. Sparse is a truncation operator that makes the weight matrix sparse. In each row, it retains the top ntop entries and truncates the others to 0. Normalize symmetrically normalizes the weight matrix. Once constructed, the weight matrix remains unchanged during training.

Using the Lie-Trotter scheme, we obtain a diffusion step (7) after the convection step (6). However, in our implementation, typically multiple diffusion steps follow each convection step. The reason is that the diffusion term has strong numerical stiffness, as shown in the online appendix A. When using a simple explicit Euler discretization method, the step size needs to be small enough to maintain numerical stability. Therefore, to maintain a certain diffusion strength, we will use a simple forward Euler scheme to discretize the diffusion term. Furthermore, even with a small total strength, multiple diffusion layers yield slightly better results in experiments. Thus, in the network, we add r diffusion layers after each residual block, with each layer having a fixed step size. The description of our Diff-ResNet can be found in Figure 1. We summarize our method in Algorithm 1.

Note 1: In the diffusion step (7), the feature map of the i-th data point depends on the feature maps of all previous data points, which is not feasible in tasks with a large total number of data points. In our implementation, we adopt a mini-batch training strategy. That is, the weights in each batch are accordingly sparsified and normalized.

IV. ANALYSIS OF DIFFUSION MECHANISM

In this section, we will analyze the effectiveness of the diffusion mechanism theoretically. To simplify the problem, we only consider binary classification, and our analysis can naturally extend to multi-class situations.

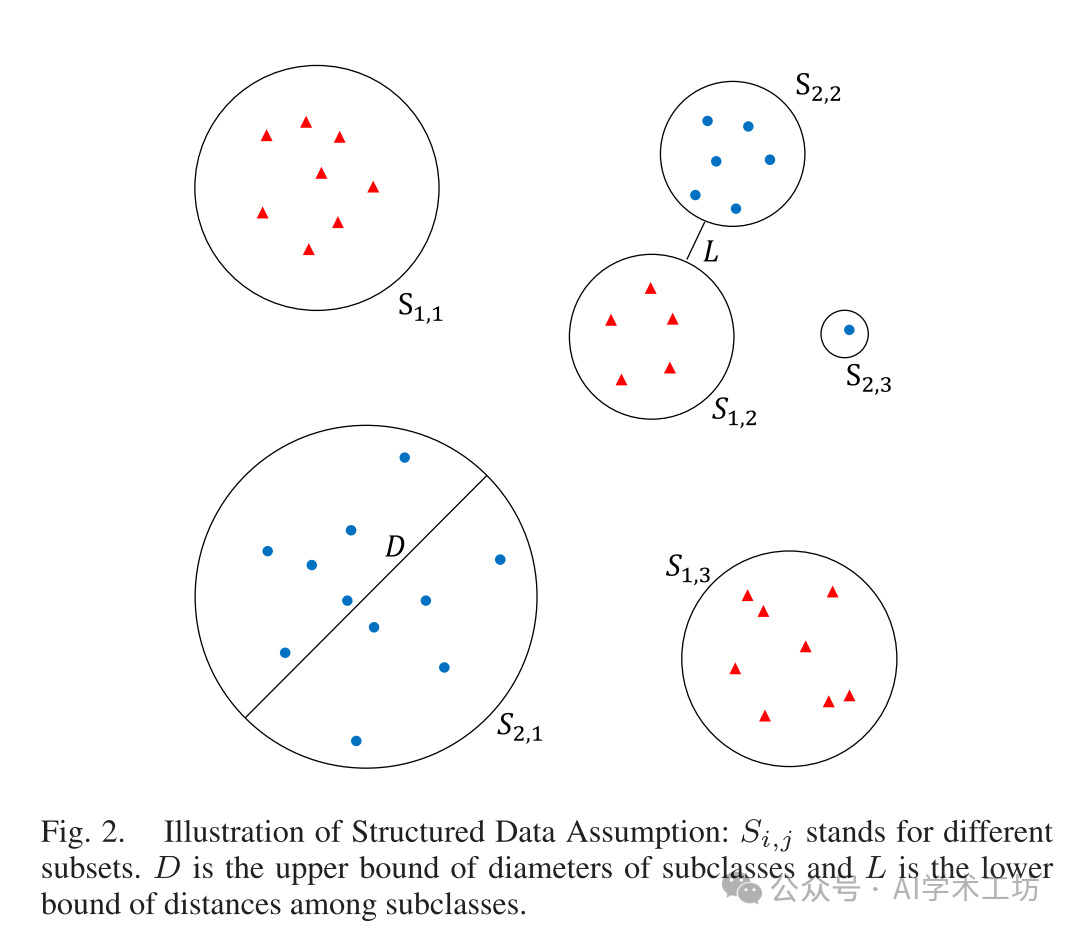
A. Structured Data Assumption

Our dataset is generated as follows: Assume all data points come from D. The symbol denotes that for all x, there exists y. Each set contains points from class C. We further assume that each set can be partitioned into several non-overlapping and bounded subsets, each corresponding to a subclass. In binary classification, C_1 and C_2 are the two classes, and k is the number of subclasses, which may vary with classes. However, we can set k to the maximum value across all classes and let non-existent subclasses be empty. Let N denote the total number of subsets. The distance between two disjoint sets is defined as

The diameter of a set is defined as

Note 2: The reason we introduce subclasses instead of directly using classes is that it can alleviate our separability assumption. We do not need two classes to be well separated from each other, which is unrealistic in real-world scenarios. Instead, we only need local subclasses to form clusters.

Now we are ready to state the structured data assumption.

(A) (Upper bound of diameter) There exists a D such that for each x, we have: for some y, then

(B) (Lower bound of distance) There exists a L such that for each x, we have

Illustration of the structured data assumption is shown in Figure 2. Here, D and L are similar to inter-class distance and intra-class distance, which are widely used terms in clustering. The difference is that the diameter used in our analysis is an upper bound of the local intra-class distance of points within subclasses. In this sense, the structured data assumption may be more suitable for handling complex datasets. For example, in the MNIST dataset, each digit may have different handwriting styles, corresponding to different subclasses, which fits our analysis framework. The intuition behind the structured data assumption is simple: similar samples should be close, while different samples should be far apart.

B. Theoretical Analysis

We present the theoretical results of this article to explain the role of the diffusion mechanism in binary classification. Due to space limitations, we defer all proofs to the online appendix.

Definition: A set S where x_i, x_j ext{ are in } S is called linearly separable if and only if there exists a hyperplane that divides the entire space into two half-spaces, with data points in each half-space having the same label.

Theorem 1: (Approximation property of ResNet flow) If all x_i can be separated by a set of k parallel hyperplanes, then there exists a unique region located between each pair of adjacent parallel hyperplanes. Then we can construct a time-dependent parameter in the ResNet flow,

such that all final regions of x_i are linearly separable. We need k different variables and layers.

We provide an overview of the proof. Consider the simplest case where each x_i contains only one point, and the width is also 1. Our main idea is to construct a ResNet flow such that each subclass is moved to an appropriate position, achieving better separability. After solving the simplest case, we extend to the case where the network width is larger. Finally, we prove the case where there is more than one point in each x_i.

In the classic XOR dataset, the original data points are not linearly separable. However, Theorem 1 tells us that through the ODE flow, we can make the output features linearly separable so that an appropriate fully connected layer can achieve accurate classification.

Our next step is to show that the conditions in Theorem 1 can be satisfied by introducing the diffusion mechanism. First, we provide a sufficient condition related to the distance-diameter ratio.

Theorem 2. If the distance-diameter ratio is large enough,

then all x_i can be separated by a set of k parallel hyperplanes.

This proof relies on comparing the surface area of a specific set with that of a unit sphere. Notably, in most cases, the number of subclasses is much smaller than k. Hence, the constant in the inequality is attainable. The next proposition shows that the diffusion step can increase this ratio at an exponential rate.

Proposition 1: Assume each subset x_i forms a connected component in the graph, and each x_i is convex. Then, the distance-diameter ratio grows to infinity, that is

Moreover, the growth rate is exponential.

The basic idea of proving Proposition 1 is to show that d_i ext{ is non-increasing} while converging to zero at an exponential rate. Utilizing spectral clustering theory, we demonstrate that each subclass converges to its center along the diffusion process.

To meet the assumption that points in each subset form a connected component in the graph, we should ensure that (1) no edges connect points in different subsets, and (2) any two vertices in the same subset are mutually connected. By constructing the weight matrix, each vertex in the graph is only connected to its k nearest neighbors. Therefore, the first argument is satisfied when k is not too large, meaning that the nearest neighbors only include points from the same subclass. On the other hand, the connectivity threshold of a k-nearest neighbor graph is [76], in our case, n should be the number of points in each subset.

The above analysis reveals that the diffusion mechanism helps to organize data points by making data points within the same subregion closer while keeping other points relatively farther apart. As the distance-diameter ratio increases, it becomes easier to distinguish data points using the ResNet flow. This property is crucial for SSL/FSL problems as it delves deep into the relationships among points.

V. EXPERIMENTS

In this section, we will demonstrate the utility of the diffusion mechanism on synthetic data and report the performance of Diff-ResNet on semi-supervised graph learning tasks and few-shot learning tasks.

A. Synthetic Data

We conducted experiments on four classic synthetic datasets: XOR, moon, circle, and spiral. In the XOR dataset, we directly applied diffusion without using any convection. We can clearly see the evolution of points, validating Proposition 1. The other three datasets are used to demonstrate the effectiveness of diffusion in classification tasks. Due to space limitations, please refer to the online appendix E.1.4 for more results.

We randomly collected 100 points located on four circles centered at (0,0), (0,2), (2,0), and (2,2) with a radius of 0.75. These four circles are considered subsets corresponding to four subclasses. The circles centered at (0,0) and (2,2) belong to the same category and are marked in red. The blue points are similarly generated from the circle centered at (2,0). Here, we show the evolution of points as the diffusion strength approaches infinity. As described in Section B, we stack diffusion steps using a small step size γ to ensure stability. In Figure 3, the distribution of points after 1, 10, 20, and 200 diffusion steps is provided. In this example, the initial diameter is D = 1.5, and the distance is L = 0.5, which does not satisfy the sufficient condition in Proposition 1 that L > D. However, as shown in Figure 3, diffusion is still effective. Data points within the same subclass converge to a single point. We also observe from Figure 3(b) that the distance-diameter ratio indeed grows exponentially to infinity.

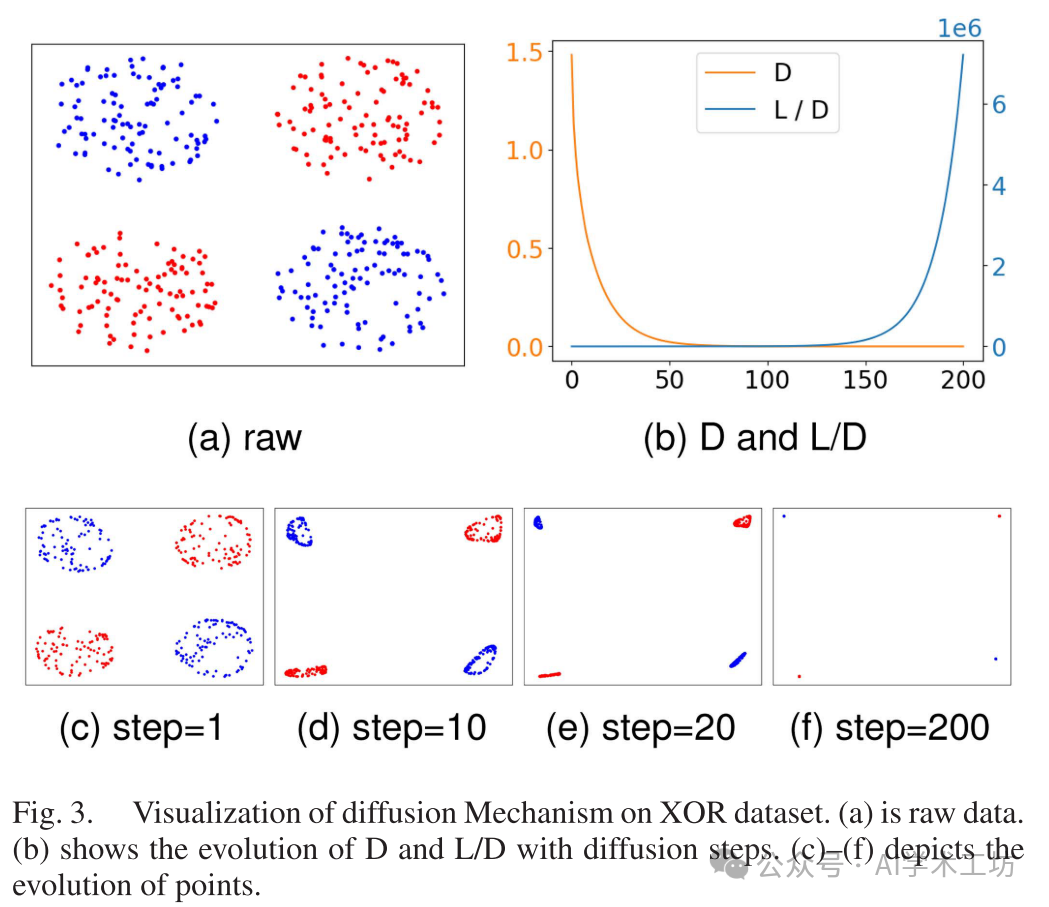
Note 3: Some may express skepticism about using the term “diffusion” since it visually creates high-density areas by clustering similar points together. However, the phenomenon shown in Figure 3 does not contradict the definition of diffusion. The energy of a point is represented by its coordinates. We expect connected neighboring elements in the graph to exchange energy until it is evenly distributed among all connected elements. Therefore, the diffusion mechanism acts to cluster points together.

Next, we demonstrate the effectiveness of diffusion in residual networks for a binary classification task containing 1000 planar data points. These points form two circles. The two categories are marked in different colors. We used a residual network with a hidden dimension of 2 (so we can conveniently visualize the features). Details of the experimental setup can be found in the online appendix E.1. In training the residual network with or without the diffusion mechanism, we plotted the feature maps before the final classification layer, as shown in Figure 4. Note that we are not plotting the input data points. Thus, even without diffusion, the points must pass through a randomly initialized residual block. Therefore, the features in Figure 4(c) differ from the original input points in (a). The results for the circle dataset are shown in Figure 4.

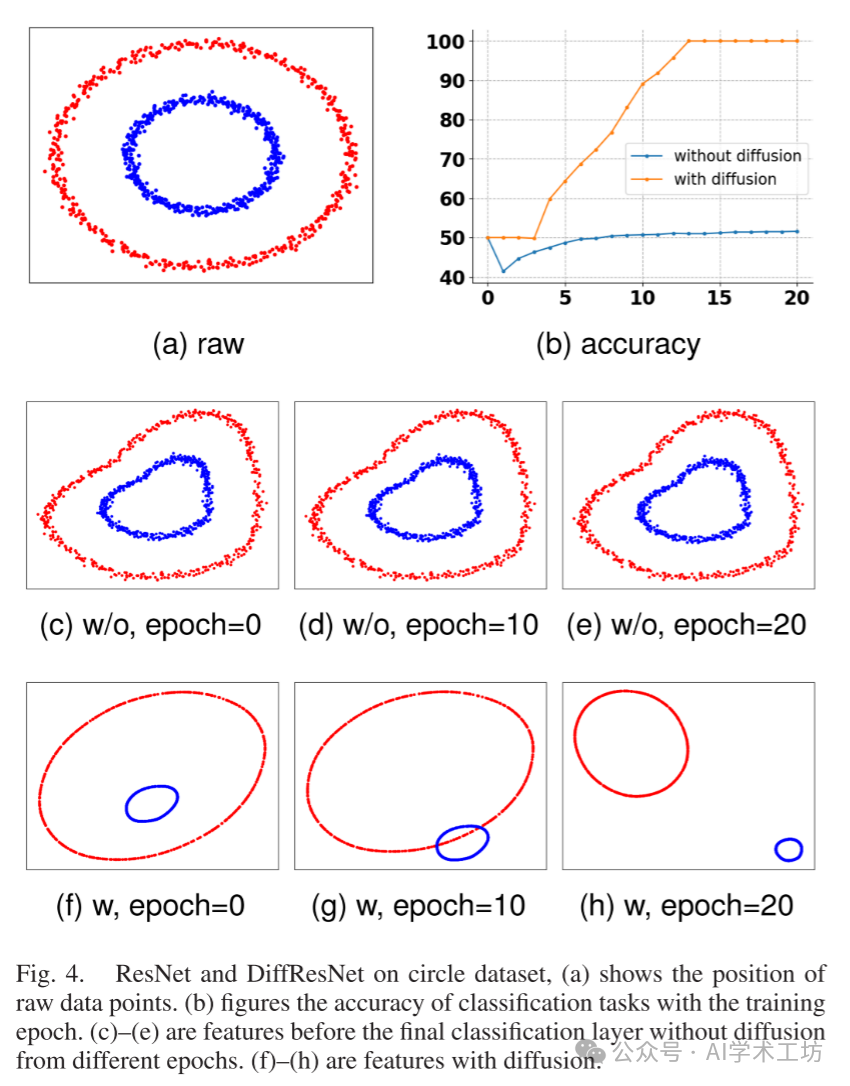
As shown in Figure 4, diffusion can reduce noise. In Figures 4(f), (g), and (h), the features are very clear, while in Figure 4(e), the features remain noisy. Additionally, the diffusion steps make the final features easier to separate. In Figure 4(h), the features can be easily separated by a straight line, while without diffusion, the features are not linearly separable, as shown in Figure 4(e). Unsurprisingly, considering that ResNet only has 18 parameters in total, the ResNet fails to provide correct classification. With the help of diffusion steps, even this small network with only 18 parameters can give correct classification, indicating that diffusion is very useful in classification problems.

B. Graph Learning

We investigated the effect of diffusion on semi-supervised learning problems in graphs. In the diffusion steps, a key point is how to determine the weights to accurately describe the relationships between data points. However, this is not an issue in graphs, as the weights are already given in the form of an adjacency matrix. We report classification results on the most widely used citation network benchmarks, including Cora, Citeseer, and Pubmed. These datasets are citation networks where nodes are documents, edges are citation links, and features are sparse bag-of-words vectors. Specific dataset statistics are provided in the online appendix E.2.1. Additionally, we did not use the fixed Planetoid [38] splits, but instead followed [77] and reported results for all datasets using 100 random splits with 20 random initializations for each split.

Mainstream methods in graph learning, such as GCN [78], GraphSAGE [79], and GAT [80], include aggregation steps that aggregate feature information from neighbors using the adjacency matrix, and then use the aggregated information to predict labels. Unlike these traditional paradigms, our method consists of convection and diffusion steps. The convection step fully utilizes label information, while the diffusion step exchanges feature information between data samples. The adjacency matrix is only used in the diffusion step.

We compare our method with several graph learning methods: the three most popular architectures GCN, GraphSAGE (with its two variants), GAT, and recent ODE-based GNN architectures, Continuous Graph Neural Networks (CGNN) [81], Graph Neural Ordinary Differential Equations (GDE) [82], and Graph Neural Diffusion (GRAND) [47]. Detailed network structures and parameter settings can be found in the online appendix E.2. The classification results are reported in Table I. Diff-ResNet significantly outperforms ResNet without diffusion (No-Diff-ResNet). The average accuracy improves by over 15%, providing strong evidence of the benefits brought by diffusion. Furthermore, although our diffusion network differs significantly from mainstream networks, our method still achieves results comparable to classical and state-of-the-art methods in graph learning. Thus, we propose an alternative path for semi-supervised graph learning problems.

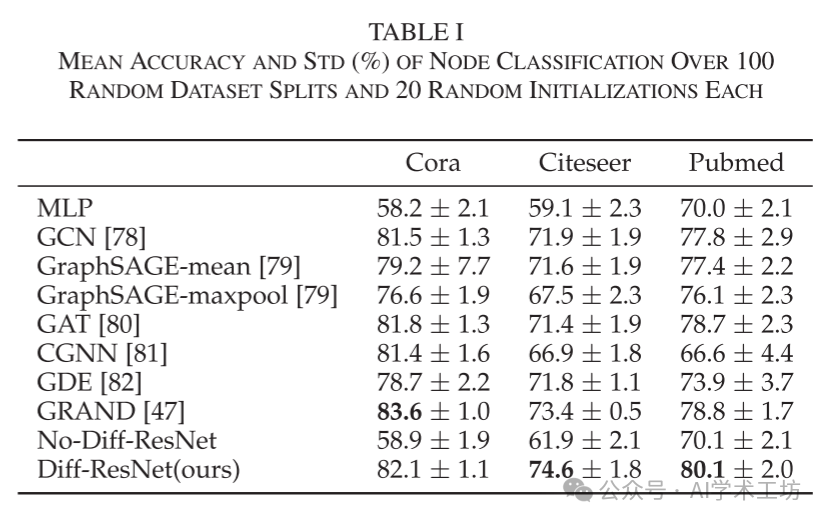
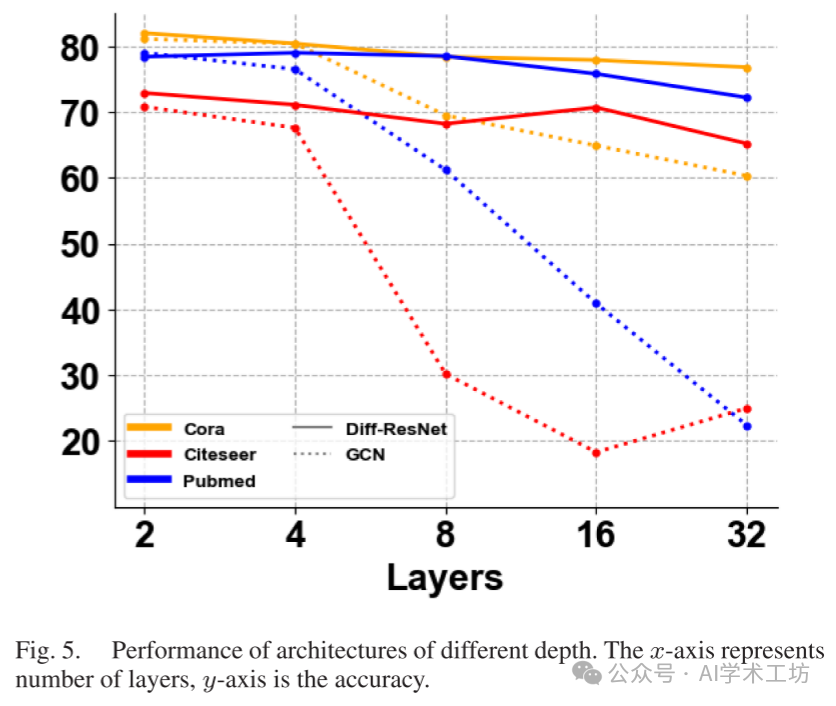
Moreover, it has been reported that methods based on neighborhood information aggregation suffer from over-smoothing as the depth increases [56], [83]. As shown in Figure 5, when the network depth increases to 32, the performance of GCN decreases by more than 50% on average. Unlike GCN, our Diff-ResNet does not use aggregation, so the representations of nodes do not converge to a single value and become indistinguishable. As the number of layers increases to 32, the performance of Diff-ResNet decreases by less than 10%, partly due to the burden of training deep networks. This demonstrates that our network structure is significantly different from mainstream architectures.

C. Few-Shot Learning

Given a dataset where S is the support set with label information, and Q is the query set without labels, the goal of few-shot learning is to find the labels of points in the query set with a very small support set. Among existing few-shot learning methods, embedding learning is a typical approach that maps each sample into a low-dimensional space, making similar samples close while keeping dissimilar samples apart. The embedding function can be learned through deep neural networks (i.e., backbone) that are pretrained on a large number of labeled examples from base categories. In few-shot learning problems, the pretrained embedding function is fixed and maps all data samples into the embedding space.

We conduct experiments on three few-shot image classification benchmarks: miniImageNet, tieredImageNet, and CUB. Both miniImageNet and tieredImageNet are subsets of the ILSVRC-12 dataset [84], with 100 and 608 classes, respectively. CUB-200-2011 [85] is another fine-grained image classification dataset with 200 classes. We follow the standard dataset splits from previous papers [68], [86], [87]. All images are resized to 84×84, following [20].

We selected two widely used networks, ResNet-18 [1] and WRN-28-10 [88], as our backbones: the latter extends the residual block by adding more convolutional layers (28 layers) and feature planes (10 times). First, we trained the backbone on base categories using cross-entropy loss, label smoothing factor of 0.1, SGD optimizer, standard data augmentation, and a batch size of 256. Note that our training process does not involve any meta-learning or episodic training strategies. The models were trained for T = 100 epochs for miniImageNet and tieredImageNet, and T = 400 epochs for CUB due to its smaller size. We used a multi-step scheduler to reduce the learning rate by 0.1 at 0.5T and 0.75T. We evaluated the accuracy of recent prototype classification on the validation set and obtained the best model. The embedding training process is generally similar to SimpleShot [68] and LaplacianShot [69], but with slight differences. Eventually, we obtained an embedding function that maps the original data points to D, where M = 512 for ResNet-18 and M = 640 for WRN-28-10.

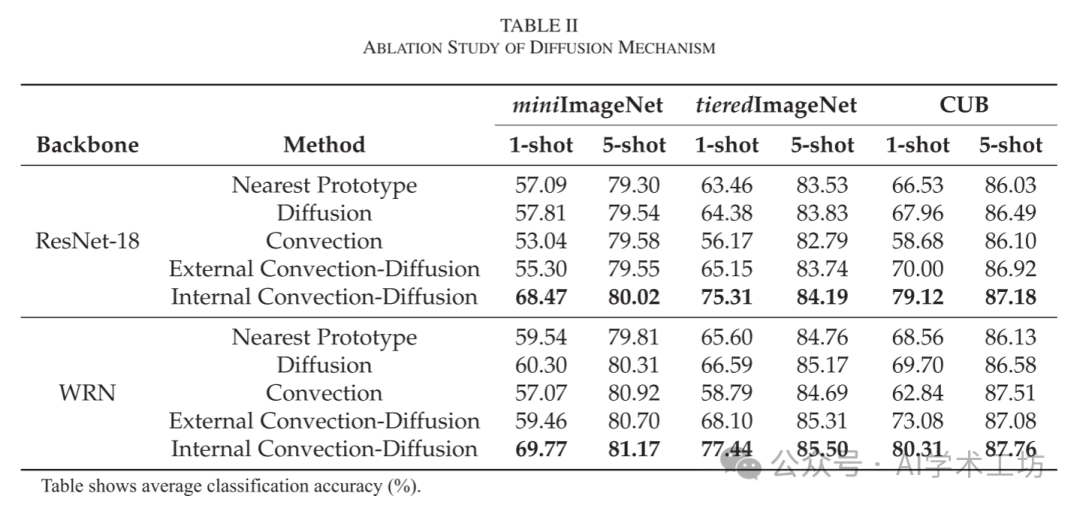
After obtaining feature vectors for each data point, we compared the performance of five typical classification methods to emphasize the effectiveness of the diffusion mechanism.

(1) Nearest Prototype: The prototype for each class is the average of the support set.

Then, if a query sample is closest to the prototype in Euclidean distance, it is classified as that class. This is the most natural classification method and serves as a baseline.

(2) Diffusion: We attempt to minimize an objective function with a Laplacian regularization term. In LaplacianShot [69], the authors optimize the following loss function

where N_q is the number of query samples. P is a label assignment in the C-dimensional simplex for each query point. d is the Euclidean distance. W is the weight between P and Q.

The first loss term is similar to nearest prototype classification. The second loss term is the well-known Laplacian regularization term. We use the iterative algorithm provided by LaplacianShot [69] to minimize the objective function. Since there are no neural networks or operations on features here, but only label propagation, we refer to this method as diffusion.

(3) Convection: We minimize the cross-entropy loss on the support set

using gradient descent and a simple 2-layer residual network. N_s is the number of support samples. Detailed network structures can be found in the online appendix E.3.2. During training, there are no relationships between data points, and the residual network corresponds to the convection ODE, so we refer to this method as convection.

(4) External Convection-Diffusion: We minimize the cross-entropy loss on the support set plus the Laplacian regularization term

using gradient descent and a simple 2-layer residual network. The difference from (3) is that we add the Laplacian regularization term in the loss function. The first Laplacian term’s variation is consistent with our diffusion term in the convection-diffusion ODE. The residual network structure corresponds to convection, while the Laplacian regularization corresponds to diffusion. Since diffusion appears externally in the loss function, we refer to this method as external convection-diffusion.

(5) Internal Convection-Diffusion: We minimize the cross-entropy loss on the support set

using gradient descent and a simple 2-layer diffusion residual network (Diff-ResNet). The loss term is the same as (3), but the difference is that we internally add diffusion layers in the network structure. By comparing (4) and (5), we aim to verify the necessity of incorporating diffusion as part of the network structure rather than as part of the loss function.

Following the standard evaluation protocol [68], we randomly sampled 1000 5-way-1-shot and 5-way-5-shot classification tasks from the test categories, with 15 query samples per category, and reported the average accuracy of the five methods mentioned above.

We visualized the features before and after diffusion in the 1-shot and 5-shot tasks using T-SNE [89] in Figure 6. The labeled data is represented by stars (support data). The unlabeled data is represented by circles. In the 1-shot scenario, we can observe that it is initially difficult to separate the points. However, with the help of the diffusion mechanism, points within the same subclass are driven closer together, making classification easier. In the 5-shot task, since the sample points already have good separability, the improvements from the diffusion mechanism are not as significant as in the 1-shot task. Nevertheless, we can verify the necessity of introducing subclasses in the structured data assumption, as the blue points are indeed divided into two subsets.

Additionally, we investigated the impact of several important parameters in the diffusion mechanism: weight truncation parameter, number of diffusion steps, and step size. We conducted experiments on miniImageNet using ResNet-18 and WRN as backbones for 1000 5-way-1-shot tasks and reported the average accuracy under different parameters.

First, we adjusted the ntop in the Sparse operation. We chose ntop = 5. The results are shown in Figure 7. From the figure, we note that it should neither be too small nor too large. A value too small may disrupt large local clusters, while a value too large may include points from different categories into the neighborhood. However, compared to the diffusion strength, classification accuracy is not very sensitive to ntop.

Next, we studied the impact of the total diffusion strength. We fixed ntop and adjusted λ, ranging from 0 to 20. The results are shown in Figure 8. Based on our experiments, we should not push the strength to infinity, as in real data, the actual data has more complex geometric structures, and we cannot expect every category to converge to a single point.

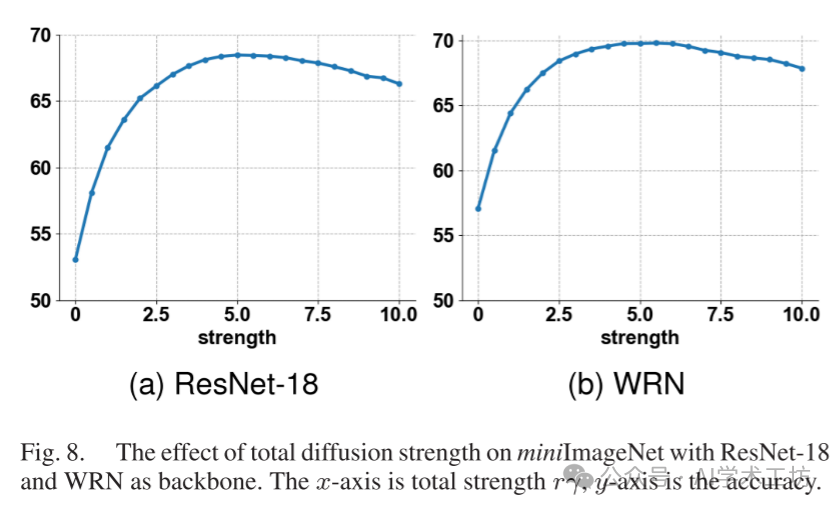
Finally, we fixed the total diffusion strength and varied the step size γ from 0 to 20 to study its impact. We required γ to ensure stability. When the total diffusion strength is too large, such as when λ = 20, we set ntop = 5. As shown in Figure 9, when the total diffusion strength is fixed, the accuracy remains almost unchanged. Therefore, stacking too many layers is not beneficial.

In summary, the performance of our Diff-ResNet mainly depends on the total diffusion strength. Under fixed strength, the number of diffusion layers and the truncation parameter have little impact on performance. We have briefly discussed the choice of ntop in Proposition 1 after Section IV-B and noted that a value neither too large nor too small is better. Rather than selecting based on different datasets or backbones, we fixed ntop and λ in all few-shot learning experiments, indicating that moderate values are sufficient to achieve good results. As for the number of diffusion layers, we determine the optimal diffusion strength by selecting it based on the validation set. From our experimental results, we need more layers for 1-shot tasks and fewer for 5-shot tasks. Additionally, the optimal diffusion strength varies by dataset, as the geometric properties differ for each dataset. Detailed parameter selection is provided in the online appendix E.3.

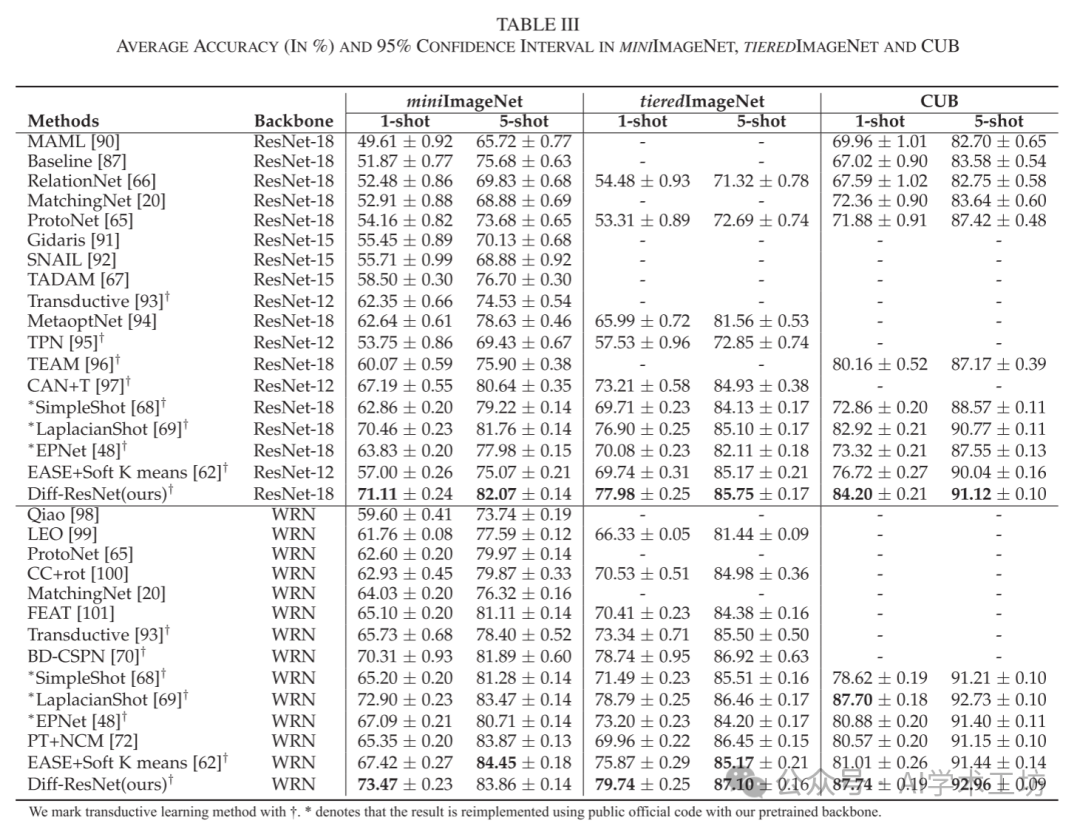
Finally, we want to emphasize that our Diff-ResNet can achieve state-of-the-art performance. To ensure a fair comparison, we adopted some techniques used in LaplacianShot [69], which are detailed in the online appendix E.3. We also removed the balanced class assumption in [62], [72] and reported the corresponding results, as our Diff-ResNet does not use such an assumption. We randomly sampled 10,000 5-way-1-shot and 5-way-5-shot classification tasks and reported the average accuracy and corresponding 95% confidence intervals in Table III. The results for networks used for comparison in Table III were collected from [68], [69], [87]. Across all datasets and various backbones, Diff-ResNet achieved the highest classification accuracy in most cases, except for the 5-shot task on miniImageNet using WRN-28-10 as the backbone. The performance improvement of Diff-ResNet on the 5-shot task is not as significant as on the 1-shot task, which is consistent with the observations in Table II. Regarding the relatively small performance boost compared to LaplacianShot [69], we have thoroughly investigated the differences between our method and theirs in Ablation Study II (Internal Convection-Diffusion vs. Diffusion).

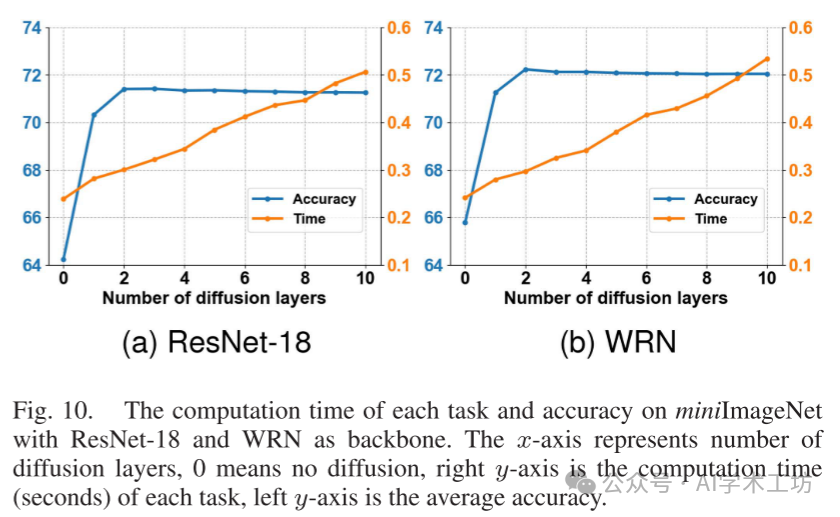
Additionally, we investigated the computational cost of the diffusion mechanism. The implementation of the diffusion layer is merely small-scale matrix multiplication, making it very efficient to use on GPUs. We ran 1000 classification tasks under different numbers of diffusion layers r and reported the average computation time per task using Diff-ResNet. The results and accuracy are reported in Figure 10. The total diffusion strength is fixed at λ = 10, unless we choose ntop = 5 to ensure stability when r = 1. We used a single GeForce RTX 2080 Ti to collect running times. As noted in Figure 9, when fixing the diffusion strength, there is no need to stack too many layers. In both subfigures, 2 diffusion layers are already sufficient to achieve optimal results, with a time increase of about 25% compared to no diffusion. Additionally, the time for 10 diffusion layers is about double that of no diffusion, with 10 layers being sufficient to achieve the desired diffusion strength in all few-shot tasks.

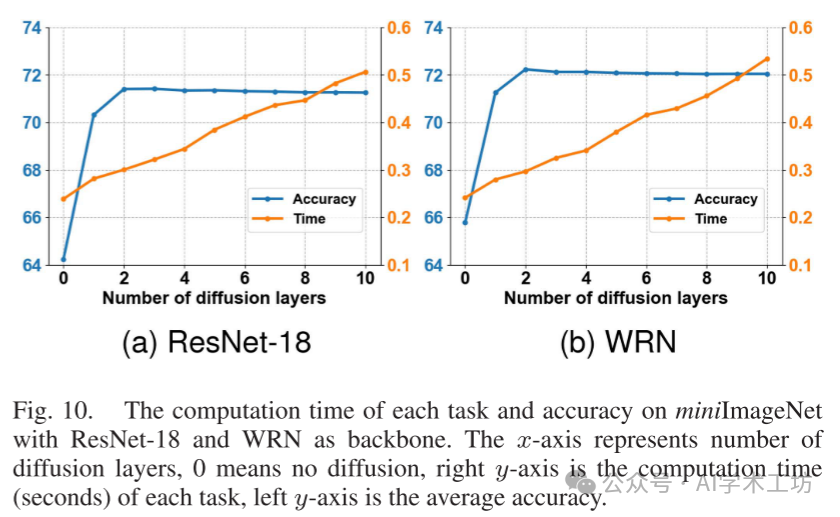
However, compared to methods such as [48], [68], [69], our method requires more time. In each few-shot task, during the inference phase, our method requires training a small neural network. Note that we are not trying to retrain or fine-tune the backbone network. Instead, we train a small network that only contains two hidden layers and one diffusion block. The acceleration of inference will be investigated in future work.

VI. CONCLUSION

In this paper, inspired by the ODE model with diffusion mechanism, we propose a novel Diff-ResNet by adding a simple yet powerful diffusion layer within the residual blocks. We provide a theoretical analysis of the diffusion mechanism and demonstrate that the diffusion term will significantly increase the local intra-class distance to inter-class distance ratio. The performance of the proposed Diff-ResNet is validated through extensive experiments on few-shot learning and semi-supervised graph learning problems. Future work involves the robustness of the diffusion mechanism, accelerating Diff-ResNet during the few-shot learning inference phase, extending from diffusion ODEs to diffusion PDEs, and exploring the effects of diffusion in semi-supervised learning with extremely low label rates.

Statement

The content of this article is a sharing of learning gains from the paper. Due to limitations in knowledge and ability, there may be deviations in the understanding of the original text, and the final content is subject to the original paper. The information in this article aims to spread and facilitate academic exchange, and its content is the responsibility of the author and does not represent the views of this account. If any content, copyright, or other issues related to works, text, images, etc., mentioned in the article are involved, please contact us in a timely manner, and we will respond and address it as soon as possible.