A Cutting-Edge Review of Diffusion Models and Knowledge Graphs

Approximately 7500 words, suggested reading time 16 minutes.
This article introduces a new knowledge graph diffusion model named DiffKG, which combines generative diffusion models with data augmentation paradigms to achieve robust knowledge graph representation learning.

The importance of knowledge graphs (graph networks) in recommendation systems is self-evident, but not all relationships are relevant to the target recommendation task. To address this issue, this article introduces a new knowledge graph diffusion model named DiffKG, which combines generative diffusion models with data augmentation paradigms to achieve robust knowledge graph representation learning.

1 Introduction

Recommendation systems are an important part of the modern internet domain, with collaborative filtering being a typical technique. However, the sparsity of user-item interactions limits recommendation performance. To address this issue, knowledge-aware recommendation techniques have emerged, integrating knowledge graph (KG) information. Despite advances in embedding-based and path-based methods, their quality highly depends on the input knowledge graph and is susceptible to noise. In response, research has utilized contrastive learning to enhance knowledge-aware recommendations, but these methods overly rely on simple random augmentation or intuitive cross-information, neglecting irrelevant information in recommendation tasks.

Therefore, effective filtering of noisy knowledge graph information and flexible encoding of user preferences is needed. We propose an innovative model, DiffKG, suitable for knowledge-aware recommendation systems. This method includes a progressive forward process, where the initial knowledge graph is gradually corrupted by introducing random noise. The incremental corruption process accumulates noise over multiple iterations, then recovers the original knowledge graph structure by iteratively denoising these noises. To address the noise problem in knowledge graphs, we introduce a KG filter to eliminate irrelevant and erroneous data, seamlessly integrating it with user preference learning. Additionally, we design a collaborative knowledge graph convolution mechanism to enhance the diffusion model by integrating collaborative signals into the knowledge graph diffusion process.

The main content of this article is as follows:

• This article proposes a recommendation model named DiffKG, which utilizes task-relevant project knowledge to enhance collaborative filtering paradigms. A new framework is introduced to extract high-quality signals from the aggregated representations of noisy knowledge graphs.

• The generative diffusion model is integrated with the knowledge graph learning framework, specifically designed for knowledge-aware recommendations, effectively combining the semantics of knowledge-aware items with collaborative relationship models for recommendation purposes.

• Extensive experimental evaluations show that the DiffKG framework achieves significant performance improvements over various baseline models on different benchmark datasets, effectively addressing the challenges posed by data noise and data sparsity.

2 Key Concepts

User-Item Interaction Graph is a graphical representation of the interaction relationships between users and items. It consists of a set of users and a set of items, each represented individually. In recommendation scenarios, this graph can be used to predict the likelihood of user-item interactions.

Knowledge Graph is a graphical structure used to organize external item attributes. It is constructed by merging the correlations and relationships of different entities and uses triples to represent the relationships between entities. Utilizing knowledge graphs allows for a more comprehensive understanding of the attributes of items and the complex relationships between entities.

KG Enhanced Recommendation Task aims to predict the likelihood of user-item interactions by training a recommendation model with learnable parameters, given a user-item interaction graph and a knowledge graph. The model predicts interaction probabilities based on user and item attributes, interaction history, and relevant information from the knowledge graph.

3 DIFFKG Framework

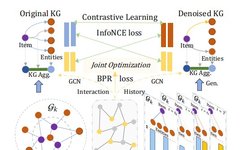
The technical design of DiffKG mainly includes three components: heterogeneous knowledge aggregation module, knowledge graph diffusion model, and KG diffusion-enhanced data augmentation paradigm. These components work together to capture various relationships within the knowledge graph and ensure high-quality recommendation information. Figure 1 shows the overall framework of the DiffKG model.

Figure 1 Overall framework of the proposed DiffKG model

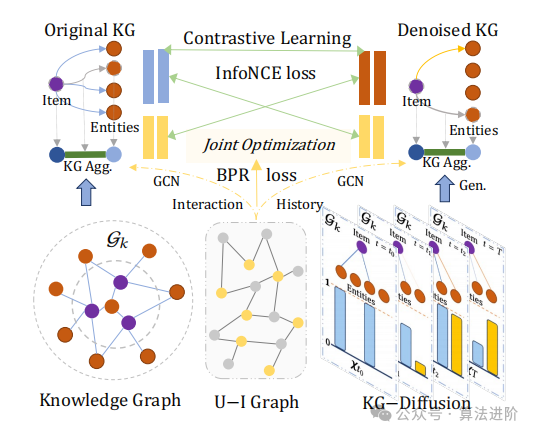
3.1 Heterogeneous Knowledge Aggregation

To address the heterogeneity of knowledge relationships in knowledge graphs, we introduce a relationship-aware knowledge embedding layer. The design of this layer is inspired by graph attention mechanisms, enabling comprehensive capture of various relationships within the knowledge graph, avoiding the limitations of manually designed paths. By combining with a parameterized attention matrix, the context dependent on entities and relationships is projected into specific representations. The message aggregation mechanism between projects and connected entities is detailed as follows:

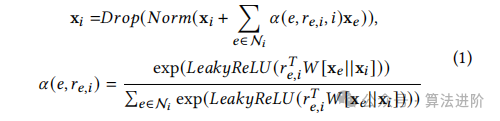
In the knowledge aggregation process, the relationships within the knowledge graph represent the neighboring entities of projects and entities, preventing overfitting by introducing dropout functions, and using _Norm_Max function during normalization. The non-parametric weight matrix is customized based on the input item and entity representations and utilizes the LeakyReLU activation function. Before heterogeneous knowledge aggregation, a random dropout operation is applied to the knowledge graph to enhance the performance of the recommendation system.

3.2 KG-Enhanced Data Augmentation

Contrastive learning has achieved significant success in the field of recommendation systems. Methods such as KGCL, MCCIK, and KGIC are knowledge graph-enhanced recommendation methods that introduce contrastive learning techniques. However, these methods rely on random augmentations or simple cross-view comparisons, which can lead to unnecessary noise and irrelevant supplemental information. In knowledge graphs, a large number of semantic relationships are crucial, but only a portion is relevant to downstream tasks. Unprocessed irrelevant knowledge can impair performance. To address this challenge, we suggest using generative models to reconstruct knowledge graph subgraphs that specifically include relevant relationships. Detailed explanations can be found in section 3.3. After constructing the relevant graph, we combine graph collaborative filtering and heterogeneous knowledge aggregation to encode user and item representations. We design a local graph embedding propagation layer, inspired by the simplified graph convolutional networks in LightGCN, described as follows:

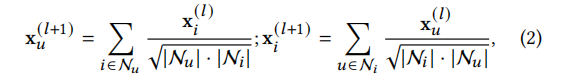
We use xu(l) and xi(l) to represent the encoded representations of user u and item i at the l-th graph propagation layer. The neighboring user/item representations are denoted as Nu and Ni. By utilizing multiple graph propagation layers, the graph-based collaborative filtering (CF) framework can capture higher-order collaborative signals. In our encoding pipeline, Gk and Gk’ are used for heterogeneous knowledge aggregation, generating feature vectors for input items while preserving the semantic information of the knowledge graph. These item embeddings are further input into the graph-based CF framework to refine their representations.

After creating two knowledge-enhanced graph views, we treat the view-specific embeddings of the same node as positive pairs (e.g., (x′u, x′′u )|u ∈ U). The embeddings of different nodes are considered negative pairs (e.g., (x′u, x′′u )|u, v ∈U, u≠ v). To achieve this, we define a contrastive loss function aimed at maximizing consistency among positive pairs and minimizing consistency among negative pairs. The contrastive loss can be expressed as:

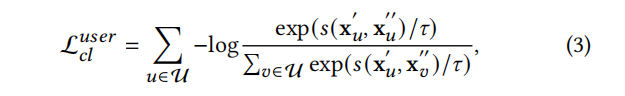
Using the cosine similarity function to measure the similarity between two vectors, denoted as s (·). The hyperparameter 𝜏, referred to as temperature, is used for the softmax operation. The user-side contrastive loss is denoted as L𝑢𝑠𝑒𝑟 𝑐𝑙, and the item-side contrastive loss is L𝑖𝑡𝑒𝑚 𝑐𝑙. By combining these two losses, we obtain the objective function for the self-supervised task, which can be expressed as L𝑐𝑙 = L𝑢𝑠𝑒𝑟 𝑐𝑙 + L𝑖𝑡𝑒𝑚 𝑐𝑙.

3.3 Diffusion Model with Knowledge Graphs

Inspired by the success of diffusion models in generating data, we propose a knowledge graph diffusion model. This model aims to generate relevant subgraphs Guncan from the original knowledge graph Gk. The model is trained to identify relationships within the knowledge graph that are corrupted by noise. By gradually introducing noise into the relationships within the knowledge graph, we simulate the corruption of relationships. Then, through iterative learning, the goal is to recover the original relationships. This iterative denoising training enables DiffKG to model the relationship generation process, reducing the impact of noise. Ultimately, the probabilities of the recovered relationships are used to reconstruct the subgraph G𝑘 ′ from Gk.

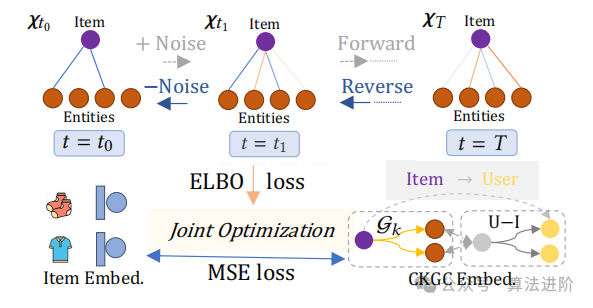Figure 2 Knowledge graph diffusion model

3.3.1 Noise Diffusion Process

As shown in Figure 2, the knowledge graph (KG) diffusion consists of both forward and backward processes and can be applied to knowledge graphs. We use an adjacency matrix to represent the knowledge graph, where the relationships between items and entities in the set Σ are indicated by binary values. In the forward process, the original structure of the knowledge graph is corrupted by gradually adding Gaussian noise, with the initial state being the original adjacency matrix of the items. In the Markov chain, by gradually adding Gaussian noise over T steps, we construct 𝝌1:T. The parameterization of the transition from 𝝌𝑡−1 to 𝝌𝑡 is:

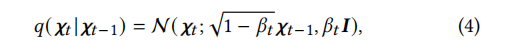
t ∈1,···,T denotes the diffusion steps, and the scale of Gaussian noise added at each step is controlled by 𝛽𝑡 ε (0, 1). As T→∞, state T converges to a standard Gaussian distribution. By utilizing the reparameterization trick and the additivity of two independent Gaussian noises, we can derive state 𝝌𝑡 from the initial state 𝝌0. The process is described as:

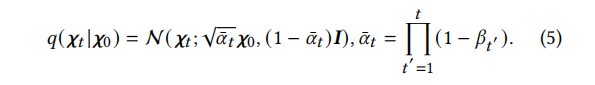
𝝌𝑡 can be reparameterized as follows:

To regulate the addition of noise, a linear noise scheduler is employed, using three hyperparameters: 𝑠, 𝛼𝑙𝑜𝑤, and 𝛼𝑢𝑝 to achieve 1− ¯𝛼𝑡. The definition of the linear noise scheduler is as follows:

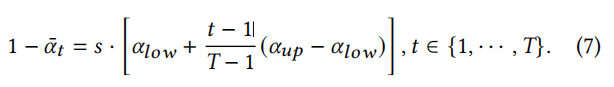
The linear noise scheduler uses three hyperparameters: 𝑠 ε [0, 1] to control the noise scale, while 𝛼𝑙𝑜𝑤 < 𝛼𝑢𝑝 ε (0, 1) sets the upper and lower limits for the added noise.

Next, the diffusion model learns to remove the added noise from 𝝌𝑡 in order to use neural networks to recover 𝝌𝑡−1. Starting from 𝝌T, the reverse process gradually reconstructs the relationships within the knowledge graph (KG) through denoising transition steps. The denoising transition steps are outlined as follows:

We utilize a neural network parameterized by 𝜃 to generate the mean 𝝁𝜃 (𝝌𝑡 , 𝑡) and covariance 𝚺𝜃 (𝝌𝑡 , 𝑡) of the Gaussian distribution.

3.3.2 Optimization of the KG Diffusion Process

To optimize the model, we maximize the evidence lower bound (ELBO) of the original knowledge graph relationships. The optimization objective of the probabilistic diffusion process is: log𝑝(𝝌0) ≥ E𝑞(𝝌1 |𝝌0 ) [log𝑝𝜃 (𝝌0 |𝝌1)].

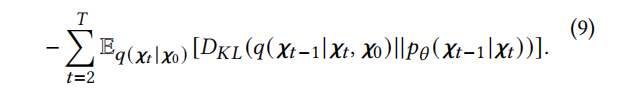
The optimization objective of the diffusion model consists of two components. The first component measures the recovery probability of 0, representing the model’s ability to reconstruct the original knowledge graph. The second component regulates the recovery of 𝝌𝑡−1 during the reverse process for 𝑡 in the range of 2 to T.

The second component in the optimization objective aims to approximate the distribution 𝑝𝜃 (𝑡−1 |𝝌𝑡) to a tractable distribution 𝑞(𝝌𝑡−1 |𝝌𝑡 , 0) through KL divergence D𝐾𝐿 (·). Following [31], the second term L𝑡 for step 𝑡 is as follows:

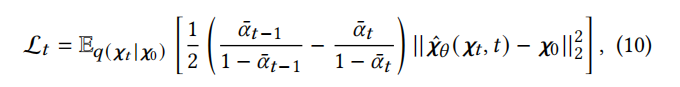
Where ˆ𝝌𝜃 (𝝌𝑡 , 𝑡) is the predicted 𝝌0 based on 𝝌𝑡 and 𝑡, implemented by a multilayer perceptron (MLP). Specifically, we use a multilayer perceptron (MLP) to instantiate ˆ𝝌𝜃 (·), which takes the step embeddings of 𝝌𝑡 and 𝑡 as inputs to predict 𝝌0. We denote the negative value of the first term in equation 9 as L𝑓𝑖𝑟𝑠𝑡, which can be computed as:

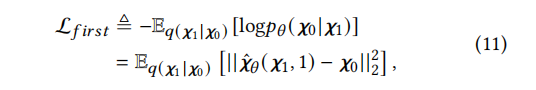
We estimate the Gaussian log likelihood log𝑝(𝝌0 |𝝌1) using unweighted -||. L𝑓𝑖𝑟𝑠𝑡 equals L1, so the first term in equation 9 can be regarded as -L1. ELBO can be expressed as -L1 – ΣT𝑡=2L𝑡. To maximize ELBO, we can optimize 𝜃 in ˆ𝝌𝜃 (𝑡 , 𝑡) by minimizing ΣT𝑡=1L𝑡. Specifically, we perform uniform sampling over step 𝑡 to optimize L𝑒𝑙𝑏𝑜 on 𝑡∼U(1, T). The ELBO loss L𝑒𝑙𝑏𝑜 is as follows:

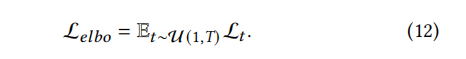
3.3.3 Generating Knowledge Graphs Using Diffusion Models

We designed a simple inference strategy for relationship prediction within knowledge graphs, consistent with the training of DiffKG. First, in the forward process, the original KG relationships are progressively corrupted to obtain T’. Then, we set ^T = T’ and perform reverse denoising, ignoring variance and using ^t-1 = μφ(^t, t) for deterministic inference. Next, we use ^T0 to reconstruct the structure of the modified KG G’k. For each item i, we select the top k^zij (j∈[0, |E | – 1], j∈J and |J | = k) and add k relationships between item i and entity j∈J. This method retains the informational structure of the knowledge graph while introducing noise in the forward process and deterministic inference in the reverse process.

3.3.4 Collaborative Knowledge Graph Convolution (CKGC)

To address the limitations of the diffusion model in generating denoised knowledge graphs relevant to downstream recommendation tasks, we propose CKGC. This method utilizes user-item interaction data, incorporating the supervisory signals of the recommendation task into the KG diffusion optimization. By aggregating user-item interaction data, the model better captures user preferences and integrates them into the knowledge graph, enhancing relevance to the recommendation task. This approach effectively bridges the gap between knowledge and recommendation tasks by incorporating user preferences into the knowledge graph diffusion optimization.

The loss function L𝑐𝑘𝑔𝑐 for CKGC is computed by aggregating user-item interaction information and the predicted relationship probabilities of the knowledge graph into the item embedding generation process. The specific steps are as follows: First, aggregate the user-item interaction information and the predicted relationship probabilities of the knowledge graph to obtain ˆ𝝌0, then update the user-item interaction matrix to integrate knowledge graph information. Next, combine the updated user-item matrix and user embeddings E𝑢 to obtain item embeddings E ′ 𝑖 that contain knowledge and user information. Finally, calculate the MSE loss between E ′ 𝑖 and the original item embeddings E𝑖, and optimize it together with the ELBO loss. The expression for L𝑐𝑘𝑔𝑐 is as follows:

3.4 Learning Process of DiffKG

The training of DiffKG includes two parts: recommendation task training and KG diffusion training. The joint training of KG diffusion includes both ELBO loss and CKGC loss components, and both are optimized simultaneously. Therefore, the loss function of KG diffusion can be expressed as:

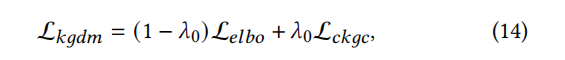
To balance the contributions of ELBO loss and CKGC loss, we introduce a hyperparameter 𝜆0 to control their respective strengths. For the recommendation task, we combine the original Bayesian personalized ranking (BPR) recommendation loss with the previously mentioned contrastive loss L𝑐𝑙. The BPR loss, denoted as L𝑏𝑝𝑟, is defined as follows:

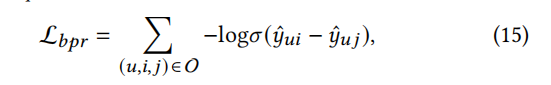
The training data is represented as O = (𝑢,𝑖,𝑗)| (𝑢,𝑖) ε O+ , (𝑢, 𝑗) ε O− , where O + denotes observed interactions, and O − denotes unobserved interactions obtained from the Cartesian product of user set U and item set I (excluding O +). Based on these definitions, the comprehensive optimization loss for the recommendation task is:

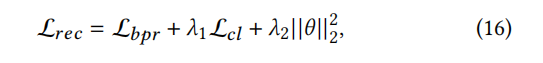
Learnable model parameters are represented as θ, which includes the trainable variables within the model. Moreover, 𝜆1 and 𝜆2 are hyperparameters used to determine the respective strengths of the CL-based loss and the L2 regularization term.

4 Experiments

To evaluate the effectiveness of DiffKG, a series of experiments were designed to investigate the following questions:

RQ1: How does the performance of DiffKG compare with state-of-the-art recommendation systems?

RQ2: What unique contributions do the key components of DiffKG make to overall performance, and how does the model adapt to changes in hyperparameter settings?

RQ3: How does DiffKG demonstrate its effectiveness in overcoming data sparsity and noise obstacles?

RQ4: To what extent does the DiffKG model provide a high level of interpretability for recommendations, facilitating a thorough understanding of its decision-making process?

4.1 Experimental Setup

4.1.1 Datasets

To ensure comprehensiveness and diversity of evaluations, we adopted three public datasets: Last-FM (music), MIND (news), and Alibaba-iFashion (e-commerce). After preprocessing with 10-core techniques, users and items that appeared less than 10 times were filtered out. For Last-FM, we used mapping methods to associate items with Freebase entities and extract knowledge triples. For MIND, we followed [24] to collect KG from Wiki data. For Alibaba-iFashion, we manually constructed the KG, utilizing category information as valuable knowledge. Detailed statistics of the three datasets and their corresponding KGs are shown in Table 1.

Table 1 Statistics of the experimental datasets

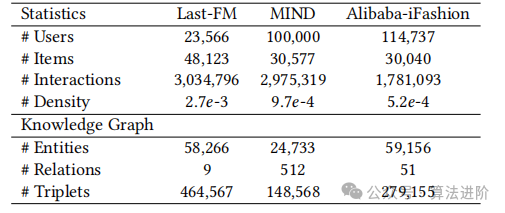
4.1.2 Evaluation Protocols

To avoid biases introduced by negative sampling in evaluations, we report performance metrics under a full-rank setting, using Recall@N and NDCG@N as top-N recommendation metrics, where N=20, which is a commonly used value.

4.1.3 Comparison Baseline Methods

To comprehensively evaluate DiffKG, we compared it with a set of baselines from different research streams.

Collaborative Filtering Methods:

• BPR: This method derives pairwise ranking loss from matrix factorization of implicit feedback.

• NeuMF: Incorporates MLP into matrix factorization to learn rich user and item representations while capturing feature interactions between them.

• GC-MC: By proposing a graph autoencoder, GC-MC utilizes the underlying graph structure to predict unknown ratings.

• LightGCN: Conducts an in-depth analysis of modules in standard GCN for collaborative data, proposing a simplified GCN model tailored for graph CF tasks.

• SGL: Introduces data augmentation techniques (e.g., random walks and feature dropouts) to generate multiple views.

Embedding-Based Knowledge-Aware Recommenders:

• CKE: Enhances the recommendation system’s understanding of item relationships by integrating collaborative filtering and knowledge graph embeddings.

• KTUP: Achieves complementary signals from collaborative filtering and knowledge graph, providing more comprehensive recommendations.

GNN-Based KG Enhanced Recommenders:

• KGNN-LS: KGNN-LS considers user preferences for different knowledge triples in graph convolutions, promoting the distribution of similar preference weights among relevant entities in the knowledge graph through label smoothing as regularization.

• KGCN: It uses GNN to integrate higher-order information, generating aggregated knowledge representations for items.

• KGAT: Introduces the concept of collaborative knowledge graphs, functioning by applying attention aggregation on the joint user-item-entity graph.

• KGIN: Models users’ relational intentions and utilizes relation-path aware aggregation to extract rich information from composite knowledge graphs.

Self-Supervised Knowledge-Aware Recommenders:

• MCCLK: A model that adopts a hierarchical contrastive learning approach, primarily used to mine useful structural information from user-item-entity graphs and their subgraphs.

• KGCL: A method that utilizes self-supervised learning to fuse knowledge graph information, effectively addressing noise issues and improving recommendation accuracy.

4.2 RQ1: Overall Performance Comparison

We evaluated the overall performance of various methods, with DiffKG performing optimally among all baseline methods, as shown in Table 2.

Table 2 Performance comparison of Last-FM, MIND, Alibaba-iFashion datasets in terms of Recall@20 and NDCG@20.

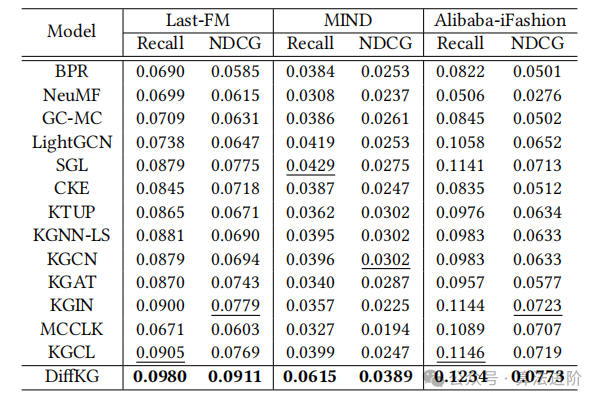
The graph diffusion model of DiffKG enhances the effectiveness of data augmentation, improving the accuracy of recommendations. Compared to traditional methods like BPR and NeuMF, DiffKG demonstrates superiority by integrating knowledge graph information. Compared to other knowledge-aware models, DiffKG exhibits significant performance advantages. This indicates that knowledge graphs often contain irrelevant relationships that may negatively impact recommendation quality. KGCL and DiffKG adopt different approaches to address the sparsity issue in collaborative filtering, but DiffKG utilizes task-relevant knowledge graphs generated through a designed KG diffusion model, demonstrating the effectiveness of the DiffKG approach.

4.3 RQ2: Ablation Studies

4.3.1 Ablation of Key Modules

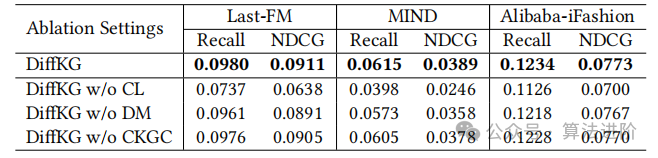
This study evaluated the effectiveness of key modules in DiffKG, developing three model variants: “w/o CL” (removing the KG-enhanced data augmentation module), “w/o DM” (replacing the diffusion model with a variational graph autoencoder), “w/o CKGC” (excluding collaborative knowledge graph convolution from KG diffusion model optimization).

As shown in Table 3, the ablation studies yield key conclusions: 1) Removing KG-enhanced contrastive learning leads to a significant performance drop, validating the effectiveness of incorporating additional self-supervised signals from knowledge graphs. 2) The ablation of the knowledge graph diffusion model component proves its crucial role in enhancing DiffKG performance, confirming the effectiveness of the diffusion process in capturing task-relevant relationships. 3) The absence of the collaborative knowledge graph convolution module results in performance degradation, emphasizing the importance of collaborative knowledge graph convolution in DiffKG, aiding in the integration of user collaborative knowledge into the training of the recommendation diffusion model. A significant performance drop was observed in the Last-FM and MIND datasets, indicating a high level of noise in their knowledge graphs.

Table 3 Ablation study of key components in DiffKG

4.3.2 Sensitivity to Key Hyperparameters

This study delved into the impact of different hyperparameters on our approach, particularly those in the data augmentation and knowledge graph diffusion modules. To visually present the results, we report the corresponding graphs on the MIND dataset, as shown in Figure 3.

Figure 3 Hyperparameter analysis on the MIND dataset

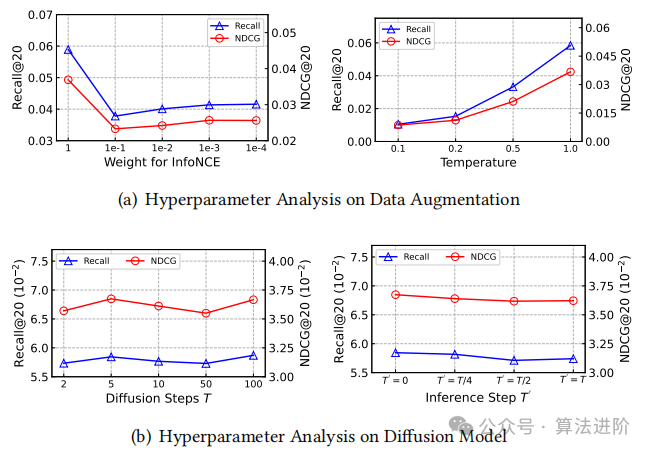
We investigated the hyperparameters of DiffKG, particularly 𝜆1 (weight of InfoNCE loss) and 𝜏 (softmax temperature). Optimal performance was achieved at 𝜆1=1 and 𝜏=1, emphasizing the importance of contrastive learning. In the knowledge graph diffusion model, increasing the number of diffusion steps had minimal impact on accuracy, as shown in Figure 3(b). To balance performance and computation, we chose T=5. Interestingly, the best performance was achieved at T′=0, avoiding excessive corruption of the original KG.

4.4 RQ3: Further Investigation of DiffKG

Sparse User Interaction Data. To evaluate DiffKG’s performance in handling sparse data, we divided users and items into five groups, each containing the same number of users, with interaction density gradually increasing from group 1 to group 5, representing different levels of sparsity. A similar approach was used for items, with test results shown in Figure 4.

Figure 4 Performance at different levels of data sparsity

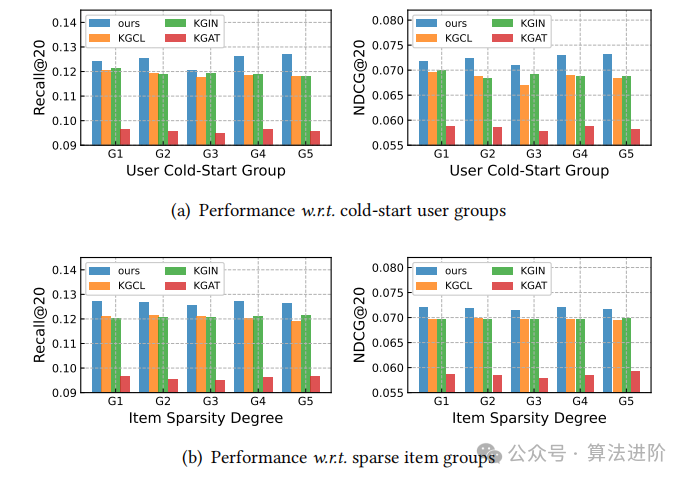
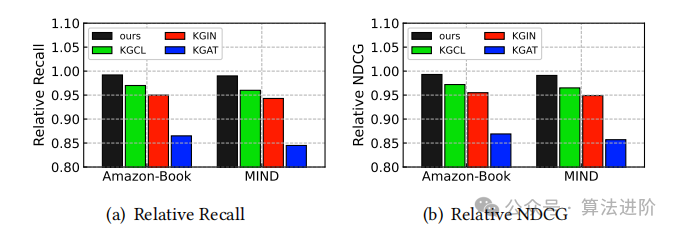
Knowledge Graph Noise. To evaluate DiffKG’s ability to filter irrelevant relationships, we injected 10% noise triples into the KG, simulating scenarios with numerous subject-irrelevant relationships. While keeping the test set unchanged, we compared the performance of DiffKG with other knowledge-aware recommendation systems.

Figure 5 Performance in mitigating KG noise

• DiffKG shows superior performance in evaluating recommendations for sparse data, outperforming KGCL, effectively demonstrating the effectiveness of KG-enhanced data augmentation. This method effectively addresses the issue of irrelevant relationships in knowledge graphs that may mislead user preference encoding.

• In recommendation scenarios with long-tail item distributions, DiffKG significantly improves recommendation performance, effectively mitigating popularity bias. Compared to other baseline methods, DiffKG outperforms competitive KG-aware recommendation systems such as KGAT and KGIN. This suggests that simply incorporating all KG information into collaborative filtering may introduce noise from irrelevant item relationships and fail to effectively alleviate popularity bias.

• The DiffKG model performs optimally among various knowledge-aware recommendation models, thanks to its generated task-specific knowledge graphs. The noise suppression effect of DiffKG is significant, as shown in Figure 5, demonstrating that even in the presence of knowledge graph noise, its performance decline is minimal, proving its ability to discover relevant information from noise. Moreover, the KG effectively supports user preference modeling.

4.5 RQ4: Case Study

We conducted a news recommendation case study, comparing results with and without the knowledge graph diffusion model. The study found that noise in the knowledge graph could introduce bias and mislead user representations. However, by combining the KG diffusion paradigm, our DiffKG effectively filtered out irrelevant KG information, resulting in more relevant news articles. These articles included discussions about Star Wars video games, actor involvement in Star Wars movies, and social media commentary on Star Wars films. By accurately leveraging and filtering knowledge graph information, our model demonstrated improved performance in recommendation tasks, illustrating its effectiveness in enhancing relevance and mitigating the impact of irrelevant information in knowledge graphs.

Figure 6 Relevant news with and without KG propagation

5 Related Work

5.1 Knowledge-Aware Recommendation Systems

Existing knowledge-aware recommendation methods include embedding-based, path-based, and GNN-based methods. Among these, GNN-based methods, such as KGCN, KGAT, and KGIN, combine the advantages of both paradigms to extract valuable information from knowledge graphs. KGCN utilizes a fixed number of neighbors for item representation aggregation, while KGAT assigns weights based on the importance of knowledge neighbors. KGIN combines user preferences and relational embeddings in the aggregation layer. These GNN-based methods leverage the powerful capabilities of GNNs and the rich information in knowledge graphs to enhance recommendation systems.

5.2 Data Augmentation for Recommendations

The combination of data augmentation techniques with self-supervised learning (SSL) has become an effective method for enhancing recommendation systems. SSL-based data augmentation techniques leverage additional supervisory signals extracted from the original data to address data sparsity and improve recommendation performance. Data augmentation methods, such as contrastive learning, generate augmented views of user or item representations, effectively addressing data sparsity issues and enhancing recommendation performance through self-supervised learning. Additionally, inspired by natural language processing tasks, masking and reconstruction augmentation techniques involve masking or hiding certain items or parts of user-item interactions, training the model to predict the missing elements, forcing the model to learn contextual relationships. Integrating SSL data augmentation techniques into recommendation systems can solve data sparsity, capture complex patterns, and enhance the generalization ability of recommendation systems.

5.3 Diffusion Probabilistic Models

Diffusion probabilistic models have shown great potential in fields like computer vision and natural language processing. In the visual domain, diffusion models excel in image generation and restoration tasks. In text generation, models are trained to recover original text from perturbed data. Diffusion models have also been applied in other areas, such as graph learning for graph generation, including continuous-time generative diffusion processes and discrete denoising diffusion models. Recently, diffusion probabilistic models have also been explored in the recommendation domain.

Edited by: Yu Tengkai

Proofread by: Lin Yilin