A Comprehensive Summary of Graph Neural Networks (GNN)

Originally from Python Artificial Intelligence Frontier

Graph Neural Networks are widely used in recommendation systems, knowledge graphs, and traffic road analysis due to their advantages in processing non-Euclidean space data and complex features. However, when the graph data volume increases, problems arise: computation becomes extremely slow, memory cannot hold it, and communication in distributed systems becomes challenging.

This article first introduces how Graph Neural Networks transmit information and discusses common GNN models and their challenges under big data. It summarizes GNN algorithms for big data, including sampling algorithms based on nodes, edges, and subgraphs. Additionally, it presents recent advancements in accelerating GNN programming frameworks, including mainstream frameworks and optimization techniques.

The organization of this article is illustrated in Figure 2:

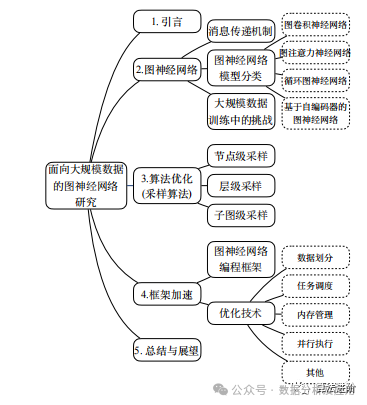
Figure 2 Organization of this article

1 Introduction

Graph structures can describe complex relationships, and graph computation can mine structural information, but they lack the capability to process node features. Neural networks excel at handling ordinary data but struggle with graph data. Graph Neural Networks combine the advantages of both, enabling the processing of graph data and predicting links, recommendations, and traffic analysis. However, large-scale graph data presents storage and computation challenges.

The challenges mainly arise from four aspects: the irregular, sparse, and dynamic structure of graph data, uneven distribution of the number of neighboring nodes; high dimensionality of node features, increasing computational and memory overhead; large data scale, leading to insufficient memory and complex data partitioning and iterative updates; hardware structure limitations, making it difficult to meet the needs for flexible reading of irregular data and efficient computation.

To address these challenges, researchers have proposed various strategies. For application scenarios, improving processing efficiency; in algorithm models, researching batch training to solve memory issues; in programming frameworks, launching DGL, PyG, etc. to solve training sample dependencies; in hardware structures, proposing optimization strategies or dedicated acceleration structures by combining CPU, GPU, FPGA, etc. These efforts help better address and alleviate the challenges of Graph Neural Networks in big data applications.

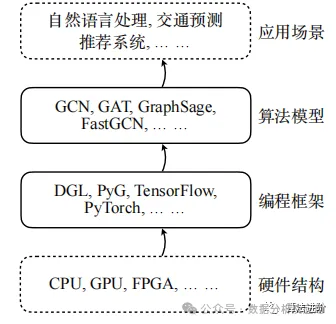
Figure 1 Overall framework of GNN

Table 1 is a related review list for this article. Among them, reviews [29-32] mainly focus on the full graph training mode of Graph Neural Network models and their applications. When the number of nodes or edges in the graph becomes very large, the entire training process may be limited by the memory of a single GPU. To solve this problem, we have sampling algorithms. These algorithms act like assistants in a puzzle game, allowing us to train in batches and handle large-scale data without exceeding the GPU memory. It’s like dividing a large puzzle into smaller parts, playing with them separately, and then putting them together.

As for the Graph Neural Network programming frameworks, they combine the characteristics of deep learning frameworks and graph structures, improving storage utilization and computational efficiency, making it easier for us to handle large-scale data. It’s like using a smarter method to play a puzzle game, allowing us to complete it faster.

Reviews [33-34] mainly summarize the development of Graph Neural Network programming frameworks. Reviews [36-38] focus more on distributed platforms, analyzing the progress of distributed GNNs in algorithm models, software frameworks, and hardware platforms. It’s like playing a puzzle game not just on one table but on multiple tables at the same time, where everyone collaborates to complete the huge puzzle together.

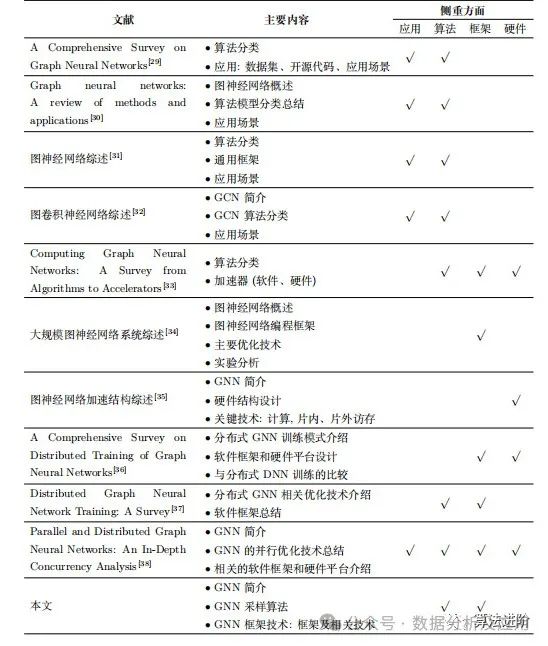
Table 1 Related reviews on Graph Neural Networks

This article studies large-scale Graph Neural Networks, providing an in-depth understanding, summarization, and analysis from the aspects of algorithm models and framework optimization. First, the article popularizes some basic knowledge of GNN and some common algorithms. Then, it summarizes GNN models with different granularity sampling strategies, as well as mainstream acceleration frameworks and related technologies. All of this aims to provide ideas and directions for future collaborative optimization of Graph Neural Networks in large-scale data applications in terms of frameworks and algorithms.

2 Graph Neural Network Models

Graph Neural Networks are neural networks specifically designed to process graph structured data, capable of combining the advantages of graph computation and neural networks, abstracting graph structural information into node features. Graph computation models excel at capturing topological structures but cannot handle high-dimensional features. Traditional neural networks deal with Euclidean space data, while graph data is non-Euclidean space, necessitating new processing mechanisms.

The message propagation model is a popular processing method in Graph Neural Networks, consisting of two steps: neighbor aggregation and node updating, which can obtain high-order neighbor information of nodes.

Common models of Graph Neural Networks include: Graph Convolutional Networks (GCN), Graph Attention Networks (GAT), Gated Graph Neural Networks (GGNN), and Self-Decoder based Graph Neural Networks (SDNE). These models face challenges such as insufficient memory and neighbor explosion during large-scale data training.

GCN aggregates neighboring nodes through convolution operations, categorized into spectral and spatial domains. GAT introduces an attention mechanism to process graph data, assigning different weights to each node. GGNN processes graph structured data based on RNNs, targeting temporal evolving graphs. SDNE applies autoencoders to learn node representations, considering the similarities between nodes.

Despite the challenges, with deeper research and exploration, it is believed that more solutions will emerge in the future.

Table 3 Challenges faced by Graph Neural Networks in large-scale data applications

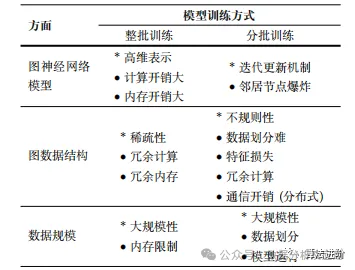
(* Indicates the main reasons for the related challenges)

3 Graph Neural Network Sampling Algorithms

To address the challenges faced by Graph Neural Networks in large-scale data training, meaningful algorithm optimization work has been initiated. Most of the work focuses on data optimization, with the primary method being the use of sampling algorithms of different granularities to achieve batch training. These algorithms can be categorized into three types based on sampling granularity: node-based sampling algorithms, layer-based sampling algorithms, and subgraph-based sampling algorithms.

3.1 Node-based Sampling Algorithms

GraphSage performs representation learning through node sampling, optimizing model parameters. It randomly samples a fixed number of neighbors for the target node, uses an aggregation function for feature aggregation, and learns through backpropagation. This method achieves new data representation and regularizes irregular graph structured data for parameter sharing.

PinSage combines random walks and graph convolution operations for large-scale recommendation systems. It constructs a computational graph through node sampling, capturing graph structural features and enhancing the scalability of graph convolutional networks on large-scale data. PinSage employs an importance-based node sampling algorithm, using random walk strategies to assess node importance and perform importance weighting.

VR-GCN is a new sampling algorithm that addresses the parameter sharing issue in large-scale Graph Neural Networks. It samples only two nodes, utilizing historically activated nodes to reduce variance, significantly decreasing the bias and variance of gradient estimation. This method greatly reduces the time and memory overhead of model training.

LGCL structures graph data to meet the requirements of convolution operations, transforming irregular graph structured data into Euclidean space for CNN algorithm optimization. However, this significant feature-based restructuring may compromise the diversity of node features, exacerbating the problem of over-smoothing in node representations.

In summary, GraphSage employs a node-based sampling algorithm, adapting to inductive tasks. PinSage uses an importance-based sampling algorithm with importance weighting. VR-GCN focuses on the convergence of sampling algorithms, reducing bias and variance in gradient estimation. LGCL filters features to reorganize them into new nodes for aggregation. These algorithms each tackle different issues within Graph Neural Networks.

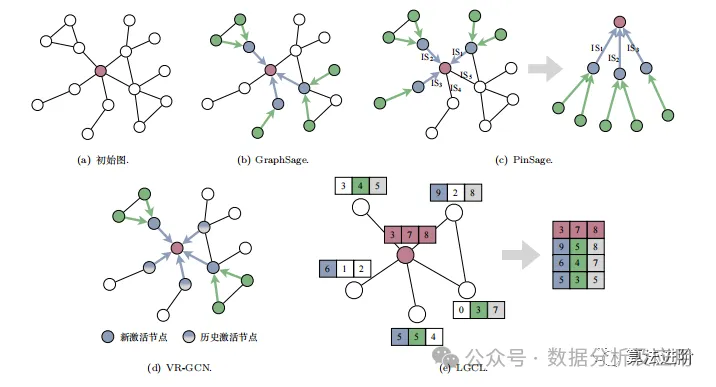
Figure 3 Node-based sampling algorithm

3.2 Layer-based Sampling Algorithms

FastGCN: Transforms graph convolution operations into probability distribution integrals and estimates using Monte Carlo methods, reducing the time and memory consumption of GCN large-scale training. It utilizes layer sampling to prevent neighbor node explosion and combines importance sampling to enhance performance.

AS-GON: Adopts adaptive layer sampling, fixing the number of sampled nodes per layer to prevent neighbor node explosion. It captures second-order similarity through connecting jumps, propagating high-order neighbor features without additional sampling overhead.

LADIES: A new sampling algorithm that constructs bipartite graphs to compute importance scores as sampling probabilities, iteratively constructing the entire computational graph to reduce computational and memory overhead.

In summary: PastGCN avoids neighbor node explosion through layer sampling but faces sparse connections and redundant node issues. AS-GCN ensures convergence and captures second-order correlations. LADIDS mitigates neighbor node explosion but has limited global node reuse.

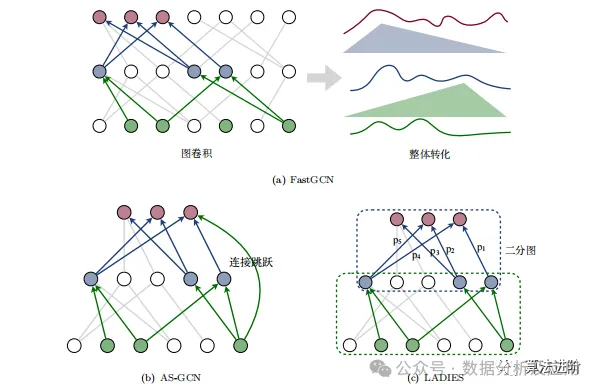
Figure 4 Layer-based sampling algorithm

3.3 Subgraph-based Sampling Algorithms

Cluster-GCN uses subgraph sampling algorithms, dividing nodes into c blocks through the Metis clustering algorithm, transforming the adjacency matrix into diagonal matrices A and B, and then decomposing the GCN function into different clusters, randomly combining blocks to reduce omissions and errors. In batch training, multiple clustered blocks are selected as training data.

RWT is a layer-wise walking training strategy aimed at reducing the time and space overhead of Cluster-GCN. It implements batch training through subgraph sampling, considering randomness and graph structural connectivity, expanding sampling layer by layer and updating subgraphs until a threshold is reached. RWT has been validated effective on GCN and GAT.

GraphSAINT is based on sampling, first sampling subgraphs and then constructing network models, eliminating batch training bias and reducing variance. It estimates the sampling probabilities of nodes and edges, sampling subgraphs in each training batch and constructing complete GON models for training. Normalization is used to eliminate bias, optimizing sampling with random walk strategies. GraphSAINT proposed by Zeng et al. improves accuracy and presents a parallel training framework to enhance program parallelism and reduce communication overhead.

SHADOW-GNN aims to address challenges in large-scale data and the over-smoothing problem. By decoupling the node acceptance region from the depth of the Graph Neural Network, it achieves the expressive power of deep networks while avoiding over-smoothing. It employs a subgraph sampling strategy to form different subgraphs and applies Graph Neural Network models of arbitrary depth on these subgraphs.

In summary: Cluster-GCN improves utilization through node clustering; RWT expands subgraphs layer by layer; GraphSAINT reduces estimation bias and variance; SHADOW-GNN enhances model scalability and mitigates the over-smoothing issue.

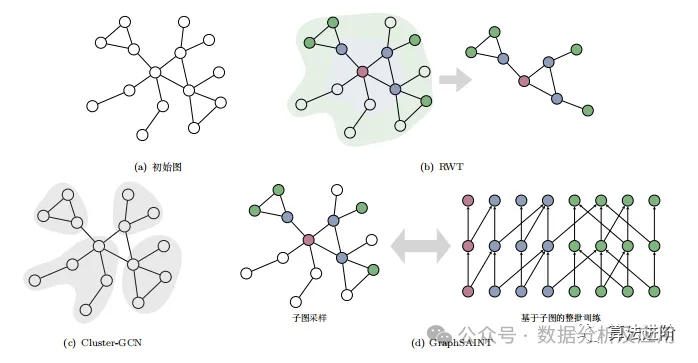
Figure 5 Subgraph-based sampling algorithm

Zeng et al. compared the accuracy performance of four sampling algorithms on node classification tasks across five datasets (Table 4), showing that subgraph-based sampling algorithms performed better across different datasets, with higher micro F1 scores and lower variance. GraphSage’s node classification accuracy on datasets such as Flickr, Reddit, Yelp, and Amazon is close to that of subgraph-based sampling algorithms, but with longer training times.

Table 4 Dataset statistics

Table 5 Node classification performance comparison

In response to the challenges faced in large-scale data training, this section summarizes different granularity sampling algorithms (as shown in Table 6), including node-level, layer-level, and subgraph-level sampling algorithms. These algorithms alleviate memory limitation issues in large-scale data training to some extent, increase model scalability, and improve model convergence through importance sampling, variance reduction, random combinations, etc. However, current sampling algorithms are primarily optimized based on static homogeneous graphs, neglecting the complexities of heterogeneity, dynamics, and power-law distributions in real-world applications.

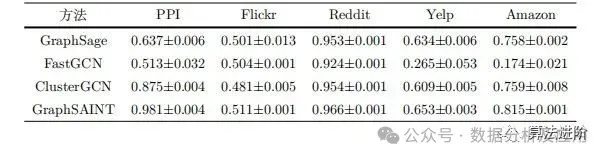
Table 6 Summary of sampling algorithms

4 Graph Neural Network Frameworks

The computation process of Graph Neural Networks involves irregular memory access and complex feature calculations, and traditional frameworks perform poorly in graph computation. To address this issue, researchers have proposed programming frameworks for Graph Neural Networks and explored optimization techniques, laying the groundwork for the operation and optimization of large-scale GNN models.

4.1 Graph Neural Network Programming Frameworks

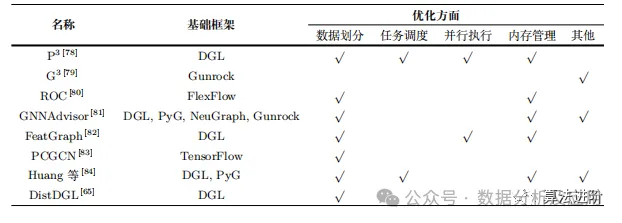
This section summarizes mainstream programming frameworks such as Deep Graph Library, PyTorch Geometric, Graph-Learn, etc., as shown in Table 7:

Table 7 Graph Neural Network programming frameworks

4.2 Optimization Techniques Related to Frameworks

Optimization techniques related to Graph Neural Network programming frameworks are categorized into five parts based on their optimization aspects: data partitioning, task scheduling, parallel execution, memory management, and others, summarized in Table 8:

Table 8 Optimization techniques related to Graph Neural Network frameworks

5 Summary and Outlook

This article first introduces four common Graph Neural Network models: Graph Convolutional Networks, Graph Attention Networks, Gated Graph Neural Networks, and Self-Decoder based Graph Neural Networks. It then analyzes the challenges these models face when processing large data and categorizes these challenges. Next, the article summarizes and analyzes existing research from the perspectives of algorithm models and programming frameworks.

First, regarding algorithm models, many optimization efforts have focused on sampling algorithms to address the challenges posed by large data in Graph Neural Network training. Based on the sampling methods, the article categorizes these efforts into three types: node-based sampling, layer-based sampling, and subgraph-based sampling. For each type of sampling algorithm, the article introduces related models and provides detailed analyses. Finally, the article offers a comprehensive summary.

Next, concerning programming frameworks, the article lists mainstream frameworks like DGL and PyG, categorizing their optimization techniques into five types: data partitioning, task scheduling, parallel execution, memory management, and others. It briefly introduces the objectives of each type of optimization technique and lists some specific strategies. Finally, the article also provides a comprehensive summary.

Looking ahead, the article summarizes the progress of Graph Neural Networks in optimizing big data, covering both model optimization and framework acceleration. Next, we will look forward to future work directions from these two aspects, as illustrated in Figure 6.

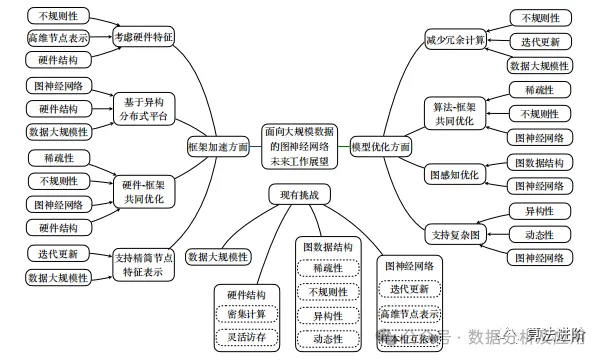
Figure 6 Future work outlook

[Disclaimer] This is a non-commercial reproduction for educational and research purposes, solely for the dissemination of academic news information. Copyright belongs to the original author. If there is any infringement, please contact us immediately, and we will delete it promptly.