Title: SPDET: Edge-Aware Self-Supervised Panoramic Depth Estimation Transformer With Spherical Geometry

Edge-Aware Self-Supervised Panoramic Depth Estimation Transformer With Spherical Geometry

Authors: Chuanqing Zhuang; Zhengda Lu; Yiqun Wang; Jun Xiao; Ying Wang

Source Code Link: https://github.com/zcq15/SPDET

Abstract

Panoramic depth estimation has become a hot topic in 3D reconstruction technology because it provides an omnidirectional spatial field of view. However, due to the lack of panoramic RGB-D cameras, panoramic RGB-D datasets are difficult to obtain, which limits the practicality of supervised panoramic depth estimation. Self-supervised learning based on RGB stereo image pairs has the potential to overcome this limitation, as it is less dependent on datasets. In this work, we propose SPDET, an edge-aware self-supervised panoramic depth estimation network that combines transformers and spherical geometric features. Specifically, we first introduce panoramic geometric features to build our panoramic transformer and reconstruct high-quality depth maps. Additionally, we introduce a pre-filtered depth image-based rendering method to synthesize new view images for self-supervision. Meanwhile, we design an edge-aware loss function to improve the self-supervised depth estimation of panoramic images. Finally, we demonstrate the effectiveness of our SPDET through a series of comparisons and ablation experiments, achieving state-of-the-art self-supervised monocular panoramic depth estimation. Our code and models can be found on GitHub.

Keywords

Edge Awareness, Monocular Depth Estimation, Panoramic Camera, Pre-Filtered Depth Image-Based Rendering, Self-Supervised, Spherical Geometry.

I. Introduction

A panoramic camera is a type of camera that can capture panoramic images with an omnidirectional field of view. Panoramic images perceive the global context and complete spatial structure of a scene, making panoramic depth estimation a hot topic in 3D reconstruction technology.

Monocular depth estimation has the potential to achieve high-precision reconstruction and good generalization capabilities on large-scale RGB-D datasets. However, constructing a large-scale panoramic RGB-D dataset is both time-consuming and labor-intensive, requiring expensive panoramic RGB-D cameras. Therefore, self-supervised learning methods based on RGB image sequences have become an important development trend, providing a low-cost solution.

Currently, some works have addressed self-supervised applications in panoramic depth estimation. NonLocal-DPT introduces self-supervision as a data augmentation method for supervised learning, but this work does not explore how to improve performance through fully self-supervised learning. SvSyn rendered a stereo panoramic dataset and verified the feasibility of using lightweight CNN models for self-supervised panoramic depth estimation in a general self-supervised framework. However, SvSyn still did not leverage the potential of self-supervised methods for accurate performance in panoramic depth estimation. Therefore, it is necessary to further investigate the application of the self-supervised process in panoramic depth estimation.

We first attempt to introduce state-of-the-art supervised models into a self-supervised framework. We observe that the characteristics and advantages shown in supervised tasks are not well utilized in the self-supervised framework, leading to weaker depth estimation results. For example, convolutional models like HoHoNet and UniFuse are unable to model effectively due to their weak fitting ability to the rich spatial structure of panoramic scenes. Meanwhile, transformer-based models such as NonLocal-DPT and OmniFusion can capture the full spatial context and long-range dependencies of panoramic images. However, these complex transformer models are difficult to optimize in a self-supervised framework because they do not effectively integrate transformers with panoramic imaging models. Therefore, we introduce spherical geometric features into the transformer to overcome this drawback and achieve accurate depth estimation through a self-supervised framework.

Overall, self-supervised methods synthesize differentiable new view images to optimize depth estimation. However, synthesized images produce mismatched supervision signals at object edges due to occlusion and de-occlusion during view transformation. Although depth image-based rendering (DIBR) filters these signals by generating visibility masks corresponding to the synthesized images, some occluded background textures still mix with foreground objects in the newly synthesized view images. Consequently, the predicted depth maps exhibit bleeding artifacts at the boundaries. Furthermore, previous panoramic self-supervised processes typically use photometric consistency loss and depth smoothness loss to train the network. However, the local window of photometric consistency loss makes it easier to get stuck in local optima in texture-less areas, especially in indoor environments. At the same time, depth smoothness loss causes the predicted depth maps to be overly smooth. Therefore, we address these issues by improving the self-supervised rendering method and loss functions.

In this work, we propose SPDET, an edge-aware self-supervised panoramic depth estimation network that utilizes transformers and spherical geometric features. On one hand, we construct a panoramic transformer with spherical geometric features. Specifically, we first introduce panoramic geometric features during the patch embedding stage to generate non-overlapping tokens. Then, we design a panoramic spatial pooling module to further aggregate the global spatial context and reconstruct the positional relationships of the tokens in space. Additionally, we propose an offset field resampling module to resample features and generate fine-grained panoramic depth maps with clear edges.

On the other hand, we propose a pre-filtered DIBR and an edge-aware loss function for the self-supervised architecture. Specifically, we first calculate the occlusion mask of the source view image through backward DIBR. Then, during the forward pre-filtered DIBR, we filter out occluded background textures to render a target view image that is not mixed, alleviating the bleeding artifacts caused by texture mixing at edges. Furthermore, we design an edge-aware loss function to mitigate local optimum issues and enhance depth edges while maintaining local smoothness of the depth maps.

In summary, our contributions are fourfold:

1. We constructed a panoramic transformer with spherical geometric features for panoramic depth estimation in a self-supervised architecture.

2. We proposed pre-filtered DIBR to synthesize un-mixed new view images for self-supervision, alleviating the bleeding artifacts at edges in self-supervised monocular depth estimation.

3. We designed an edge-aware loss function to mitigate local optimum issues and retain better depth structures.

4. Our self-supervised process SPDET, as shown in Figure 1, achieves state-of-the-art self-supervised monocular panoramic depth estimation.

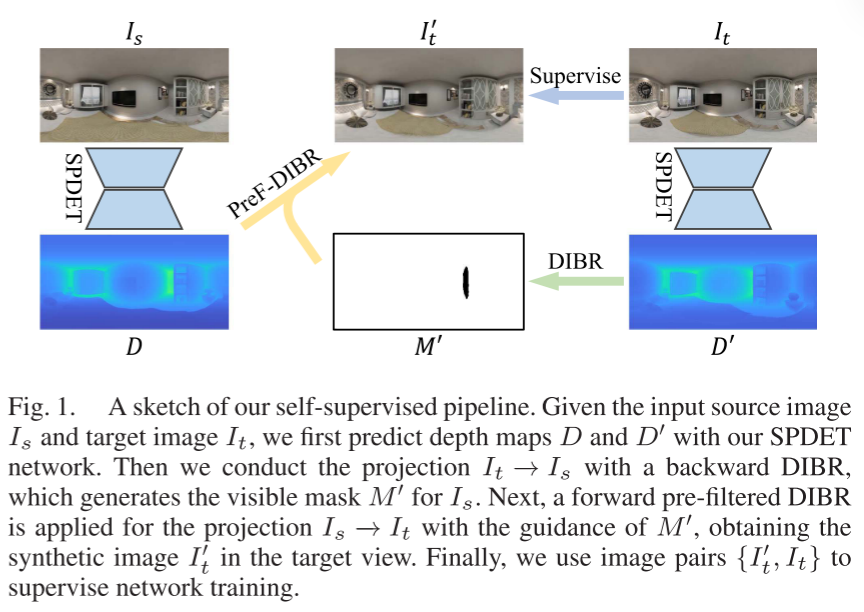
III. Method

For self-supervised monocular panoramic depth estimation, we propose SPDET, which consists of a panoramic transformer, pre-filtered depth image-based rendering (DIBR), and an edge-aware loss function. In this section, we first describe the spherical imaging model of panoramic cameras. Then, we introduce a panoramic depth estimation network that combines transformers and spherical panoramic geometric features to model the full spatial context of panoramic images. After that, we propose a pre-filtered DIBR method to filter out texture mixing and synthesize new view images as supervision signals. Finally, we propose an edge-aware loss function to alleviate the local optima and over-smoothing issues in previous self-supervised loss functions.

A. Panoramic Imaging Model

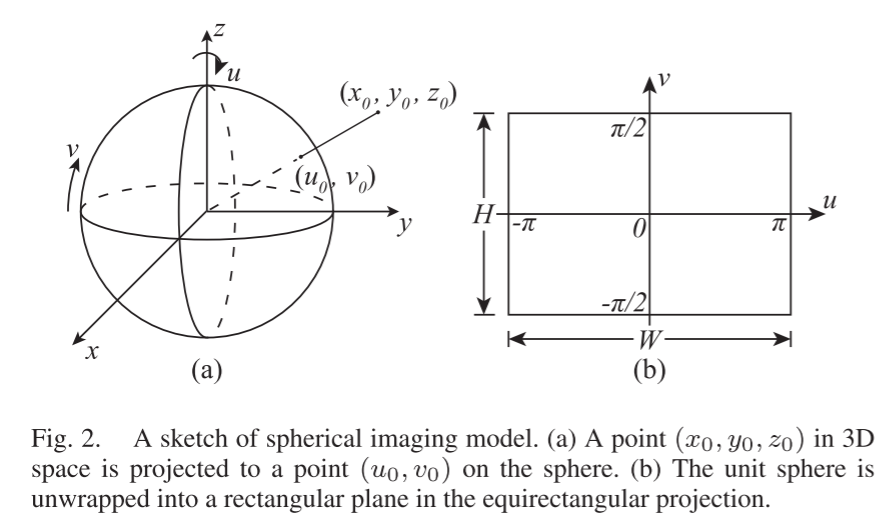
In the panoramic imaging model, objects in 3D space are projected onto a unit sphere located at the camera center. As shown in Figure 2(a), let the Cartesian coordinates of point P be P = (x, y, z) ∈ R^3, then its azimuthal angle u ∈ [-π, π] and polar angle v ∈ [-π/2, π/2] are projected onto the sphere as follows:

where atan is the arctangent function.When we sample the sphere according to the (u, v) coordinates, as shown in Figure 2(b), the imaging results on the sphere are unfolded into a panoramic image, defined as an equirectangular projection (ERP).Conversely, given the planar projection coordinates (u, v) of a point p in the panoramic image and its depth value d ∈ [0, ∞), the corresponding 3D point P = (x, y, z) is calculated as follows:

B. Panoramic Transformer with Spherical Geometry

The architecture of our panoramic transformer is shown in Figure 3(a), which includes geometric-aware embedding, transformer encoder, panoramic spatial pooling, and convolutional decoder. Given an input panoramic image, we first use a ResNet50v2 encoder and a geometric embedding module to convert it into tokens. Next, we utilize transformer layers to model the global context. After that, we propose a panoramic spatial pooling module to further aggregate the anisotropic global spatial information. Finally, we use a convolutional decoder and fusion blocks to generate predicted depth maps and offset field resampling.

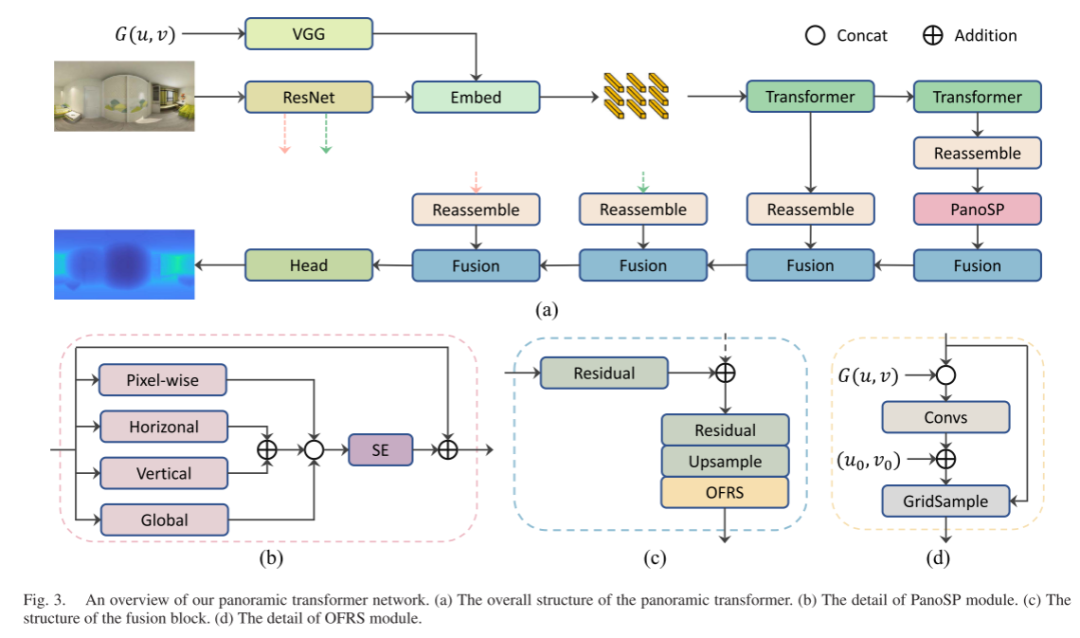
1. Geometric Embedding (GeoEmbed): To guide the transformer to model the full spatial context of panoramas, we designed a geometric embedding (GeoEmbed) module to embed panoramic geometric features with tokens. Given an input panoramic image I, we first use ResNet50v2 as the backbone network to generate tokens for the transformer layers. Note that the backbone network extracts feature maps at downsampling levels of 1/4, 1/8, and 1/16, denoted as R1, R2, and R3, respectively. The first two features are passed to the decoder through a reassembly layer, while the last feature of size 1024 × H/16 × W/16 is transformed into tokens.Additionally, we attach a spherical coordinate branch to provide panoramic geometric information during feature extraction, as shown in Figure 3(a). To represent the ERP coordinates (u, v) as continuous spherical feature maps, u and v each require two trigonometric functions sin(·) and cos(·) to represent their original phase information. Furthermore, the joint representation of u and v represents a point on the sphere, while a single one cannot represent it. Therefore, we introduce the geometric information and spherical coordinates representation as follows:To embed the geometric representation into the feature space, we input G(u, v) into the VGG19 network and extract geometric features of size 256 × H/16 × W/16. To accommodate the 5D input G(u, v), we replaced the first convolutional layer of the VGG19 network with a new convolutional layer whose input channel is 5, and we randomly initialized the parameters. Other layers are initialized with parameters pre-trained on ImageNet. Afterward, the VGG19 network is trained together with the complete model.Next, the feature map FMLP is flattened into a token set {t1, t2, …, tN}, where N = HW/256 is the number of tokens. Finally, a readout token t0 and a learnable positional encoding set {p0, p1, …, pN} are appended to the token set. Thus, the final token set T is represented as:
2. Transformer Encoder: To extract global information from the panoramic image, we use a transformer encoder to model the long-range dependencies between tokens. First, the token T is passed through a series of 12 transformer layers to model long-range dependencies and aggregate global information, where the tokens after the 9th and 12th layers are selected as transformer outputs, denoted as T9 and T12, respectively. To leverage global information and reconstruct image-like feature maps, we merge t0 into {t1, t2, …, tN} using a readout operator as follows:The output N tokens are flattened into a 2D feature of size 768 × H/16 × W/16. Before passing the 2D feature maps {R1, R2, T9, T12} to the decoder, a reassembly layer transforms its channels to 256, and a convolution with a stride of 2 downsamples T12 to 256 × H/32 × W/32.
3. Panoramic Spatial Pooling (PanoSP): Although the transformer effectively models the global context and introduces positional encoding to maintain the positional information between tokens, it does not explicitly introduce the adjacency relationships between tokens like convolutional networks do. Moreover, both the transformer and convolutional layers do not pay attention to the directional differences in longitude and latitude in the ERP coordinates. To this end, we propose a panoramic spatial pooling (PanoSP) module to further aggregate the global spatial information while preserving the positional relationships of tokens in space, as shown in Figure 3(b).Specifically, taking T12 as input, we use four pooling modules of different scales to aggregate spatial information, each followed by a 1×1 convolution. These pooling modules include pixel-level pooling (i.e., no processing), longitude average pooling, latitude average pooling, and global average pooling, with their output features denoted as Fp, Flon, Flat, and Fg, respectively. Afterward, an SE layer is introduced to enhance features with channel attention as follows:Finally, the output channels are compressed to 256 for subsequent use in the convolutional decoder.
4. Convolutional Decoder: The convolutional decoder uses input features {T'{12}, T9, R2, R1} to predict depth maps. First, in the lowest resolution fusion block, T'{12} is upsampled after two residual units as input for the next fusion block, as shown in Figure 3(c). Then, in the next resolution fusion block, T9 is passed through a residual unit and added to the upsampled T’_{12}. Afterward, the resulting features are passed through another residual unit and upsampling operator as input for the next fusion block. This process is repeated in the next two fusion blocks.The bilinear interpolation upsampling in the fusion block samples the feature map on the sphere at the ERP coordinates (u, v). However, its sampling points (u’, v’) do not reflect the optimal sampling locations in the spherical feature space (c, u, v), where c is the channel index. Therefore, we propose an offset field resampling (OFRS) module to resample the feature maps guided by spherical geometric features, focusing on the key feature points, as shown in Figure 3(d). Specifically, given input features Fi, we first introduce the geometric map G(u, v) to provide spherical geometric information. Then, we add two convolutional layers to predict the resampling offset field as follows:

The resampled feature map is computed as follows:where (u0, v0) is the standard grid of panoramic image coordinates.After four stages of the convolutional decoder, the feature map is upsampled to a size of 256 × H/2 × W/2, and the final decoder head upsamples the features to H × W and estimates the depth map D of the input image I. Additionally, we use CircPad for boundary padding in all convolutional layers of the network and utilize GELU activation in the convolutional decoder.

C. Pre-Filtered Depth Image-Based Rendering (Pre-Filtered DIBR)

Given the input source image Is in the source view S and the target image It in the target view T, the depth prediction network generates a depth map D for Is. First, we scatter Is to view T to obtain the new view image and establish the supervision signal for DIBR. First, for each pixel pi in Is, we compute the corresponding 3D point Pi using (2). Then, Pi is projected into view T as follows, where Rs, ts, Rt, and tt are the rotation matrices and translation vectors for views S and T, respectively. Thus, the middle pixel position is expressed as:

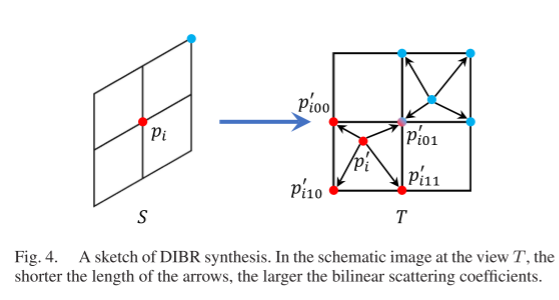
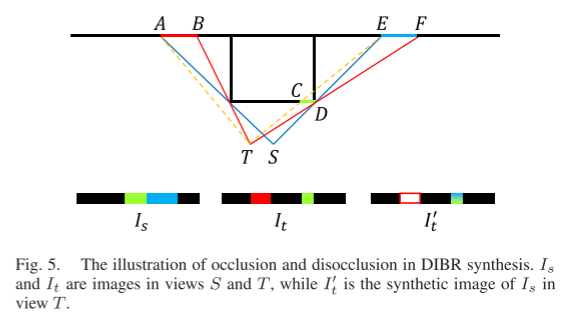
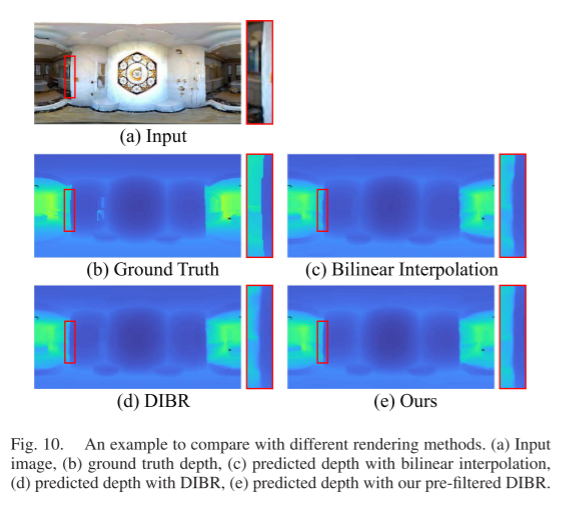
As shown in Figure 4, DIBR utilizes scattering weights Wij to distribute the color of pi to the four neighboring pixels around I’_t. The weights Wij are expressed as:where wij is the bilinear scattering coefficient from p’i to p’ij (the same as the bilinear interpolation coefficient), and dmax is set to 10 meters in all experiments.After scattering all pixels in Is, we obtain a set of colors and a set of weights for any pixel pj in the image. The synthesized image for pixel pj is:where ρ is the probability threshold to determine if the pixel is rendered. Similarly, we compute the effective pixel mask M in image I’_t as:However, the synthesized results of DIBR have defects, which we illustrate with a simple diagram as shown in Figure 5. First, AB is occluded in Is but visible in It. Then, AB is not rendered in I’_t, and when we project Is into I’_t, DIBR generates a mask M (see the red box) where = 0. Meanwhile, the projected CD and EF mix in I’_t (see the mixed green and blue), as they are visible in Is and scattered to the same location in I’_t. Therefore, the synthesized signal of CD is ambiguous and leads to bleeding artifacts near depth edges in self-supervised learning.

As shown in Figure 6, the walls and doors in Figure 6(a) mix with the bookshelf when projecting Is into I’_t, resulting in the blurry results shown in Figure 6(c) when using DIBR.

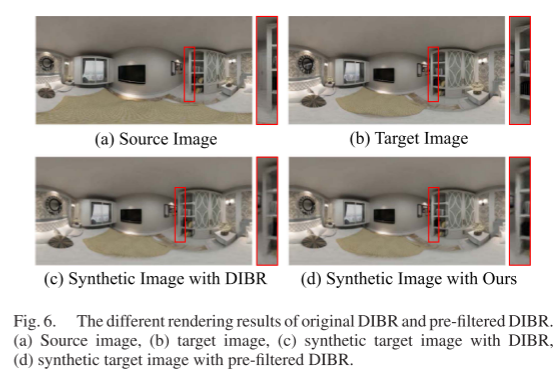
To address this issue, we propose pre-filtered DIBR to eliminate the ambiguity of the synthesized signals CD. By inputting Is and It, the projections S → T and T → S have opposite characteristics, where AB is occluded in view S but visible in view T, while EF is visible in view S but occluded in view T. We first predict the depth map D’ for image It and perform the projection T → S to obtain the mask M’ of T → S, where M’_EF = 0. Then we combine M’ with the projection of S → T, and (12) and (13) are modified as follows:Ultimately, the introduced mask M’ filters out the components rendered in I’_t by the region EF in Is, producing clear and reliable textures for CD, and the filtered visibility mask generates clear and reliable textures.

D. Edge-Aware Loss Function

To effectively constrain the obtained D and, previous self-supervised frameworks used photometric loss Lphoto and depth smoothness loss Lsmooth to train the network, as follows:where α is set to 0.85, and the window size for SSIM in experiments is 7.However, Lphoto mainly focuses on information in small local windows. Thus, it is slower to optimize based on depth bilinear interpolation coefficients in texture-less areas. Meanwhile, SSIM and L1 loss always produce similar values in local windows in texture-less areas and cannot supervise the network in these regions, making it easier to fall into local optima. Moreover, depth maps guided by Lsmooth tend to be overly smooth everywhere, whether near edges or not. To overcome these issues, we propose an edge-aware loss function that includes content term Lc and structure term Ls to train our network.First, we optimize the similarity between Lphoto in the content term and It. Additionally, to guide the network to escape local optima faster, we apply VGG features with large receptive fields and high-level features to construct perceptual loss as follows:where VGG_i(·) refers to the feature map after the i-th layer of the VGG19 network, and we choose i ∈ {3, 8, 13, 22, 31} in all experiments, with corresponding weights alphai of {1/26, 1/48, 1/37, 1/56, 1/1.5}. Therefore, the content loss Lc is expressed as:On the other hand, relying solely on the similarity between I’_t and It cannot accurately reflect the spatial structure of the scene. Therefore, we designed the structure loss Ls, which consists of gradient smoothness term Lgrad and edge-aware term Ledge, achieving a balance between the smoothness of the depth map and structural richness. Both are calculated using the scattering coordinate grid (u, v) of Is in view T.Specifically, we first convert the coordinate grid p’ = (u’, v’) of Is projected to It into a continuous representation on the sphere as follows:Then we extract the gradients ∇S(p) and ∇I_s. According to the derivative rules of trigonometric functions, S(p’) retains the components of trigonometric functions. Accordingly, we use trigonometric functions to weight the gradients of Is as follows:Moreover, Lgrad and Ledge are expressed as:Afterward, the structure loss Ls is computed as:Finally, the complete edge-aware loss function in our network is:where we set ω1 = 1.0 and ω2 = ω3 = ω4 = 0.1 in experiments.

IV. Experiments

In this section, we first introduce the implementation details of our experiments. Then, we provide quantitative and visual comparisons with state-of-the-art methods. Finally, we perform ablation experiments to verify the effectiveness of our network structure and self-supervised strategies.

A. Implementation Details

We implemented our network on the PyTorch platform. The network was trained for 30 epochs with the Adam optimizer at lr = 0.0001 and (α, β) = (0.9, 0.999) in each experiment. In addition to comparing with self-supervised works, we also trained state-of-the-art supervised models in the self-supervised framework for comparison. These comparative experiments were conducted on the 3D60, PNVS, and PanoSUNCG datasets, with image sizes of 256 × 512, batch size of 64, and conducted on 8 NVIDIA TITAN RTX GPU devices. Finally, we quantitatively evaluated the results using the spherical weighted metrics from [12], with our method inferring depth maps at a speed of 19.8 fps, parameters of 141.9 M, and GPU memory of 1,892 M. To ensure fair comparisons, we adjusted some training strategies of comparative works. In particular, we did not use CNN-predicted camera poses but used the prior camera poses in the dataset to reproduce these methods. Additionally, we transferred supervised models to our self-supervised framework and trained with the loss functions from Section III and hyperparameters from Section IV.

1. 3D60: 3D60 is a large-scale synthetic dataset rendered from real and synthetic datasets including Matterport3D, Stanford2D3D, and SunCG. It contains stereo pairs of over 20,000 viewpoints, with virtual cameras placed at center, right, and above viewpoints, with a fixed baseline distance of 0.26 meters. In our experiments, we used a real subset that includes scenes from Matterport3D and Stanford2D3D, and the training strategy follows their official splits. Additionally, we provide results for testing scenes from Matterport3D and Stanford2D3D.
2. PNVS: PNVS is synthesized from models in the Structured3D dataset. Each source view corresponds to a room and can be rendered to up to three target views. Meanwhile, the dataset is divided into two subsets, including an easy subset where translation vector t ∈ (0.2 meters, 0.3 meters) is along random directions, and a difficult subset where t ∈ (1.0 meters, 2.0 meters). We train and test on both subsets separately and use the official data splits.
3. PanoSUNCG: PanoSUNCG is a panoramic indoor video dataset collected from SunCG. It contains 80 training scenes and 23 testing scenes, with each scene consisting of 5 camera trajectories. The entire dataset includes approximately 25,000 images, along with corresponding depth maps and camera poses.

B. Comparative Experiments

In this section, we first compare the quantitative and visual results of different models on several datasets, and then we perform cross-dataset generalization tests.

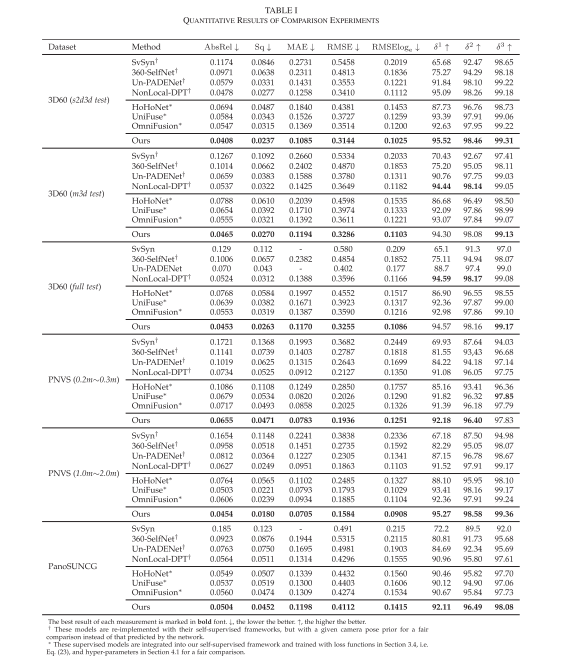
1. Quantitative Comparison: This subsection compares the quantitative results on the 3D60, PNVS, and PanoSUNCG datasets, as shown in Table I. On the 3D60 dataset, the camera moves vertically or horizontally by fixed steps, and most models perform well. Our SPDET achieves the best performance on both the full dataset and the subsets, surpassing the second place by 13.5% on the AbsRel metric and 15.6% on the MAE metric. Compared to other transformer-based methods, we embed spherical geometric features into the model to adapt to the depth structure in panoramic views. Therefore, our SPDET network can better model the scene structure of panoramic images and achieve more accurate depth estimation. On the PNVS and PanoSUNCG datasets, transformer-based models NonLocal-DPT and OmniFusion perform worse than the convolutional model UniFuse, while our network still maintains the best performance. Thus, we achieve more accurate depth predictions by combining the panoramic imaging model with transformer networks, rather than relying on large-scale model parameters.
2. Visual Comparison: In this subsection, we visualize the estimated depth maps to compare the performance of different models. As shown in Figure 7, our method effectively extracts the global context and scene structure of panoramic images, producing structured walls and complete furniture objects, such as beams in row 2, refrigerators and cabinets in row 5. Meanwhile, the offset field resampling module generates better panoramic upsampling results, allowing depth maps to separate adjacent objects and obtain clear object edges, as seen in rows 3 and 4 with the sofa and table.

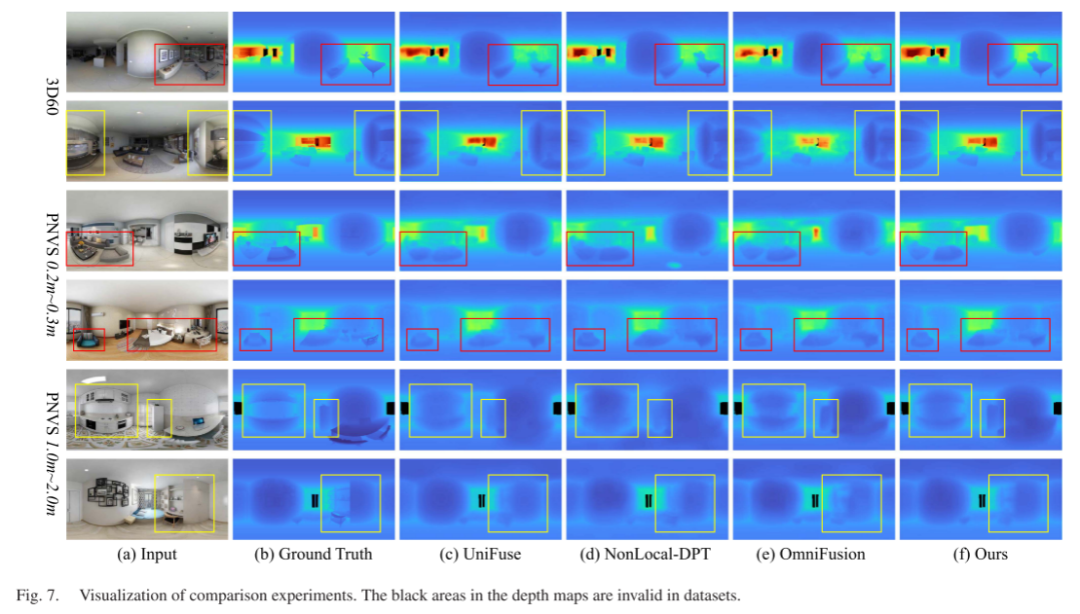
Furthermore, we notice that complex transformer models like NonLocal-DPT and OmniFusion are more difficult to optimize in self-supervised settings than other convolutional models like UniFuse, leading to their inability to reconstruct regular scene structures and flat walls in rows 5 and 6. In contrast, the spherical panoramic geometric features in our panoramic transformer guide the network to effectively perceive the spatial structure of the scene, making it easier to train good self-supervised results. Finally, OmniFusion reprojects panoramic images into overlapping image blocks, causing inconsistent depth prediction results in overlapping areas. Our model avoids inconsistencies between depth patches by constructing tokens without overlap, achieving smoother objects.

1. Model Generalization: The importance of self-supervised depth estimation lies in generalizing the model to real scenes through large-scale training data. We conducted quantitative generalization tests on the 3D60 and PNVS datasets, and then visually compared the models trained on PNVS with real video sequences in 360Video. As shown in Table II, when evaluated across datasets, the performance of all models is worse than the metrics reported in Table I. This is because when monocular depth estimation models receive unknown objects in new scenes as input, it is challenging to determine whether the textures in the image are located on the object surface or have spatial structures. Nevertheless, the accuracy and generalization of our model surpass those of other models. The proposed SPDET has superior abilities to perceive the geometric structure of the scene, rather than merely using complex models to capture the distribution of training data.

   

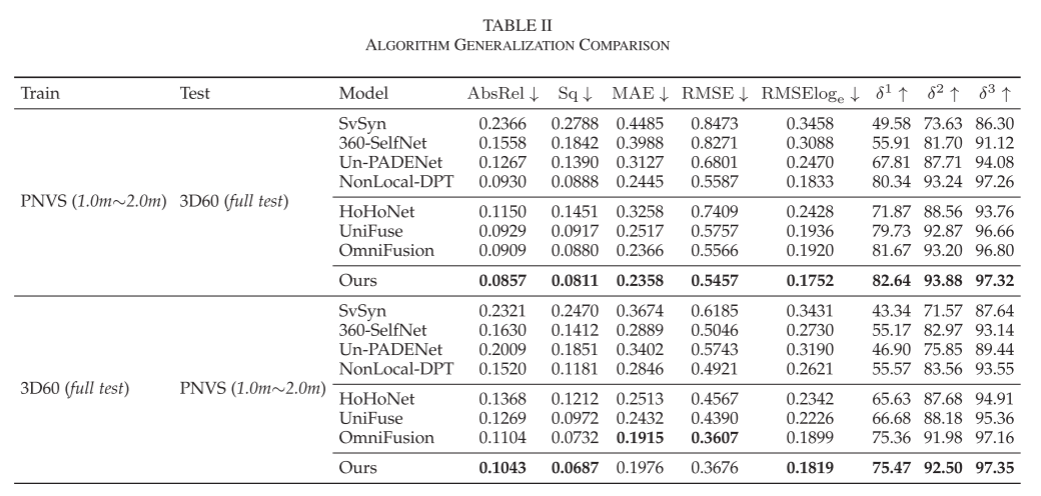
Figure 8 further demonstrates the advantages of our SPDET, which reconstructs more complete and clearer furniture depth, such as the chairs in rows 2 and 3 of Figure 8. Additionally, we observe that fixed fixtures located below the camera are reconstructed as different depths across different models and scenes. In the first two rows, the camera fixtures tend to be identified as furniture in the room, while in the last row, they are identified as textures on the floor.

C. Ablation Studies

In this subsection, we conduct ablation experiments on the 3D60 dataset regarding the network structure, spherical geometric representation and embedding, loss functions, pre-filtered depth image-based rendering, and model complexity. These experiments comprehensively investigate the role of each individual module and component in our SPDET network, with comparative analyses demonstrating the effectiveness of our approach.

1. Network Structure: We first examine the functionality of different modules in our network, as shown in Table III and Figure 9. We use DPTHybrid as the baseline model and then sequentially add GeoEmbed, PanoSP, and OFRS from Section III to construct our panoramic transformer.

   

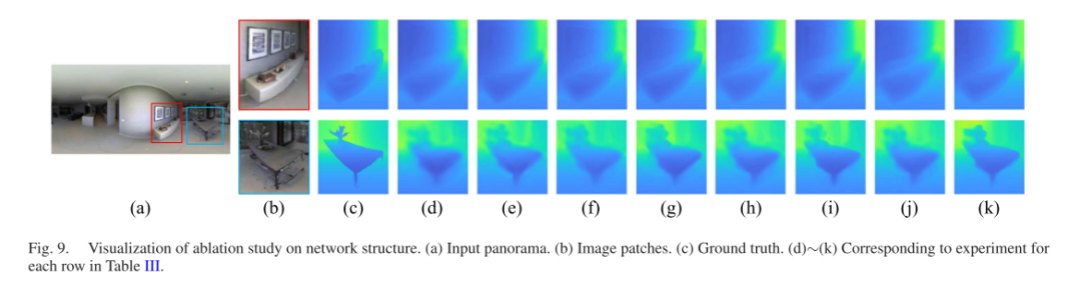
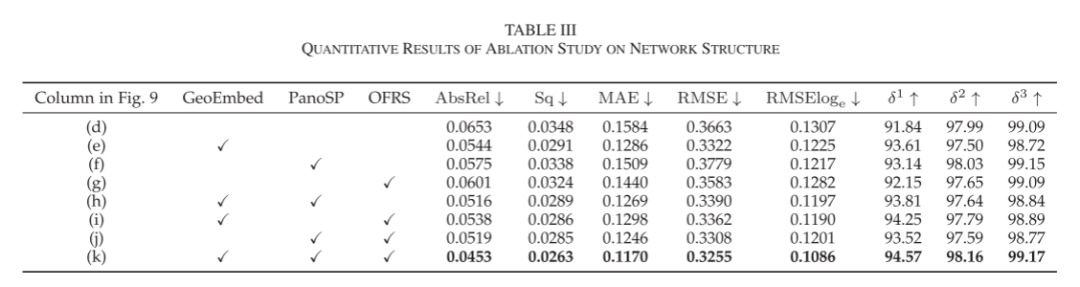
   Since the GeoEmbed and PanoSP modules focus on the global context of panoramic images, we can reconstruct more complete structures compared to DPTHybrid (see Figures 9(d)-(f)). Then, the OFRS module reconstructs fine-grained depth maps with clearer boundaries by optimizing the upsampled feature maps, as shown in Figure 9(g). However, OFRS is susceptible to unstructured textures in local windows, producing unnecessary geometric structures, as seen in the unnecessary planes outside the mural in the first row of Figure 9. Additionally, this issue is effectively mitigated by combining the GeoEmbed and PanoSP modules, which can extract global information (see Figures 9(i) and (j)). Finally, our panoramic transformer combines the above three modules, yielding the best results, as shown in Figure 9(k).

Furthermore, we also investigate the contribution of each pooling in the PanoSP module. As shown in Table IV, the global feature Fg and directional features Flon and Flat enhance the perception of spatial structure in PanoSP, significantly impacting depth estimation. In contrast, the contribution of local feature Fp is minimal, as the fine-grained features lost due to pooling can be recovered after skip connections. Interestingly, retaining one of Flon and Flat does not improve but rather reduces accuracy. This also indicates that focusing solely on the global features in a single direction cannot effectively handle the full spatial structure. A similar situation occurs with HoHoNet, which aggregates global information in compressed horizontal features, leading to many banded structures in its depth maps.

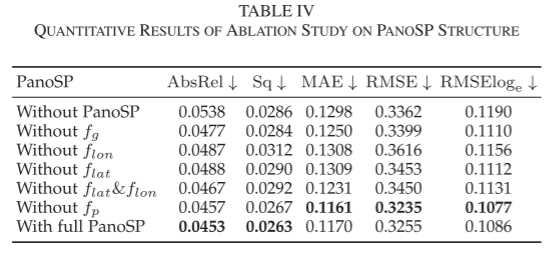
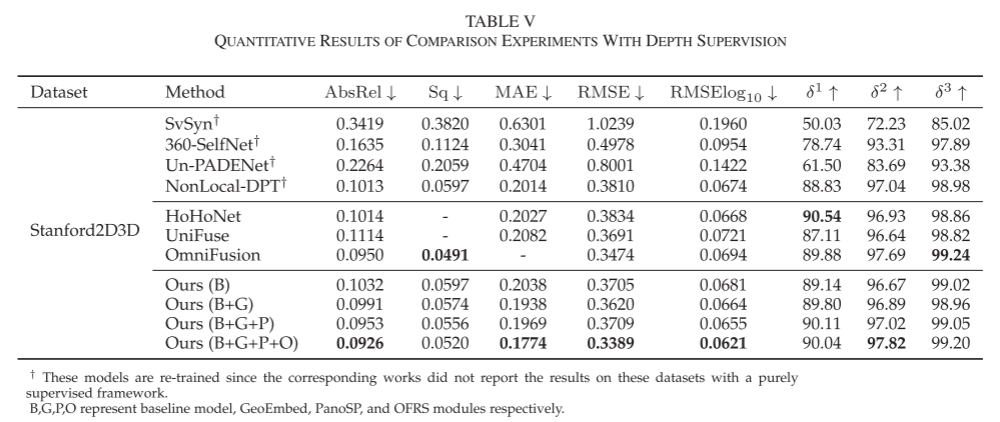
1. Performance Under Depth Supervision: To further demonstrate the effectiveness of the model design, we tested the performance of the model on Stanford2D3D and discussed the effects of different proposed network structures. We adopted the same loss function, optimizer, and hyperparameters as UniFuse. Note that for fair comparison, we follow the depth evaluation metrics in previous supervised works, i.e., metrics without spherical weighting. As shown in Table V, our complete model outperforms other models across nearly all evaluation metrics. It improves the AbsRel metric by 2.5% and the RMSE metric by 2.4%. Additionally, we observe that the accuracy of the results gradually improves with the introduction of different structural designs, which is consistent with the characteristics we observed in self-supervised settings, further validating the effectiveness of the model design.
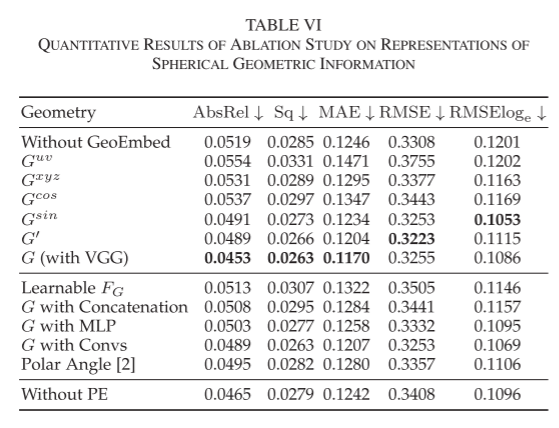
2. Spherical Geometric Representation: To demonstrate the effectiveness of the spherical geometric information represented by G(u, v) in the GeoEmbed and OFRS modules, we compared the impact of different geometric representations in Table VI. These representations include:

   

1. Continuous spherical geometric representation with continuous poles
2. Discontinuous spherical geometric representation with discontinuous poles
3. Sine function
4. Cosine function
5. Spherical normal vector grid
6. UV coordinate grid

Among these, Guv, Gsin, and G’ have discontinuous representations at the poles of the sphere, which disrupt the spatial integrity and continuity of the panoramic feature maps, affecting the scene structure of the depth maps. Then, Gcos and Gsin’s trigonometric functions lose some phase information of the image coordinates (u, v), weakening the guiding role of spherical geometric features in GeoEmbed and OFRS. Furthermore, the spherical normal vector grid Gxyz, i.e., 3D points on the unit sphere, introduces erroneous 3D spatial information, making it ineffective. In contrast, our representation focuses solely on the 2D positional information on the ERP plane and maintains the continuity of the spherical geometric features, achieving the best results.We also replaced the VGG network in GeoEmbed with different lightweight embedding modules, including direct connections, MLPs, convolutional layers, and polar angle embeddings in 360SD-Net. First, direct connections, i.e., inputs without learnable modules, only provide positional information of a point without contextual spatial structure, which is consistent with the role of positional encoding. Thus, it fails to provide geometric guidance and introduces interference information to the model. Similarly, using MLPs and directly learning geometric features FG as tensors to provide single-point positional information also performs poorly. Subsequently, using convolutional layers to extract contextual features or input polar angle geometric information as in 360SD-Net further improves performance. However, since the parameters are randomly initialized, they cannot extract sufficiently rich features compared to the pre-trained VGG. Meanwhile, polar angles cannot represent the 2D positional information in images, so the model cannot effectively obtain the spatial relationships between different pixels.Finally, we discuss the differences between the geometric embedding using VGG and the learnable positional encoding in the transformer. According to the 7th row and the last row in Table VI, both geometric embedding and positional encoding (PE) are important, providing very different positional information. Geometric embedding contains context, while positional encoding represents the positional information of individual elements of tokens. Meanwhile, their distributions and optimization directions in the feature space are inconsistent. Geometric embedding consists of contextual features extracted by the VGG19 model from G(u, v), constrained by the parameter space of the VGG19 model, while positional encoding has the potential to optimize to any point in the feature space.

1. Edge-Aware Loss Function: In this subsection, we investigate the different components of the edge-aware loss function and compare it with common loss functions in existing works to demonstrate its effectiveness, as shown in Table VII.

   

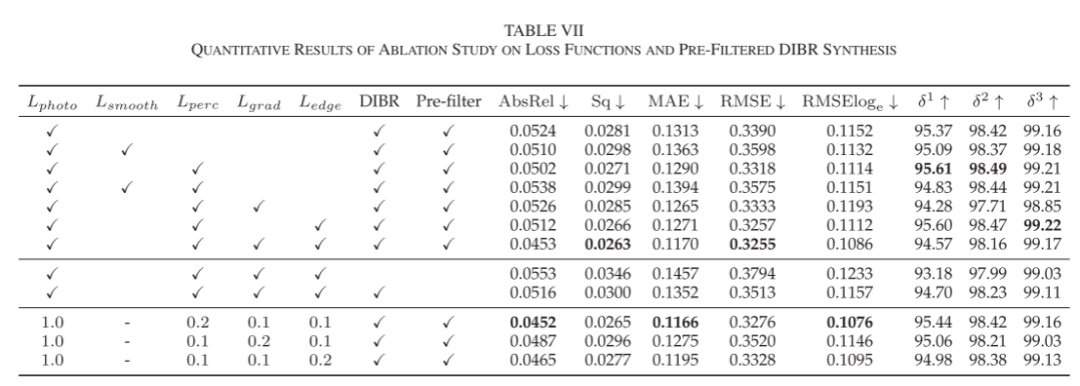
First, the basic photometric consistency loss Lphoto is affected by texture-less areas, making it difficult to estimate accurate depth maps in these areas. Then, the depth smoothness function Lsmooth and perceptual loss Lperc both alleviate this issue, as seen in the first three rows of Table VII. The difference is that Lsmooth propagates depth values from Lphoto with strong confidence in textured areas to less confident texture-less areas, while Lperc achieves higher feature discrimination in texture-less areas. Additionally, Lsmooth cannot further improve the performance of Lperc, as it tends to be overly smooth, as shown in the comparison of rows 3 and 4 in Table VII.We also observe that using Lgrad and Ledge alone is ineffective and may even lead to worse results, as their optimization directions are inconsistent with the global optimization direction. The gradient smoothness term Lgrad constrains the smoothness of the depth map and also tends to be overly smooth. In contrast, the edge-aware term Ledge preserves the depth edge structure but makes the depth map uneven on textured planes, leading to excessive sharpening and erroneous depth edges. They operate in smooth areas and edge areas, respectively, thus requiring an appropriate combination of weights to compensate for each other’s deficiencies (see rows 5, 6, and 7 in Table VII). This characteristic is also reflected in the traditional smooth loss Lsmooth, whose tendency to be overly smooth leads to worse results under the premise of introducing perceptual loss (compare row 4 with row 3 in Table VII).We further discuss the impact of different loss function weights, where a larger smoothing coefficient for Lgrad or a larger sharpening coefficient for Ledge can affect the extraction of structural edges. Essentially, the gradient smooth loss Lgrad and edge loss Ledge can accelerate convergence in texture-less areas and maintain sharp edges during training, but neither is optimized for the optimal solution, thus producing results that are overly smooth or overly sharpened with larger coefficients. In contrast, perceptual loss Lperc has a better optimization direction, and variations in weight coefficients have a minimal impact on the results.

1. Pre-Filtered DIBR: The appropriate rendering process for training image pairs has a significant impact on the accuracy of self-supervised depth estimation, especially at object edges. Here we compare different rendering methods. As shown in rows 7-9 of Table VII, using bilinear interpolation for backward deformation reports the worst results, as it cannot identify mismatched pixels between the two views. When using DIBR rendering in SvSyn, depth-weighted occlusion filtering reduces the interference of occluded textures in the synthesized images. However, occluded textures still retain in the synthesized image with less weight. Our pre-filtered DIBR eliminates texture mixing caused by occlusion in the rendered target view, generating clear and reliable supervision image pairs. This significantly alleviates the bleeding artifacts at edges in self-supervised depth estimation, making edges clearer and improving the metrics in Table VII. We also visualize this result in Figure 10, where the depth edges of the wall are clearer and sharper when gradually eliminating texture mixing through DIBR and pre-filtering during training, rather than diffusing into the background.
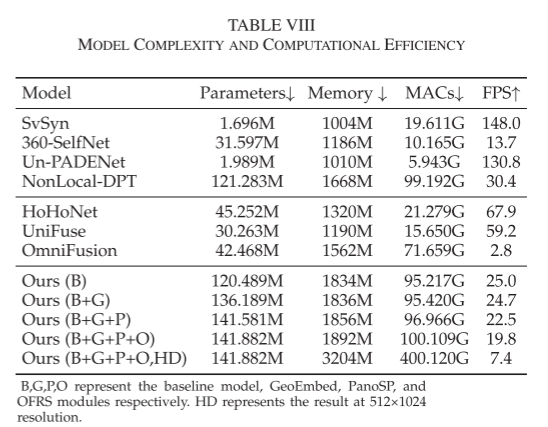
2. Model Complexity and Computational Efficiency: Here we compare the model complexity and computational efficiency of different methods, as shown in Table VIII. The proposed GeoEmbed, PanoSP, and OFRS modules introduce 13.0%, 4.5%, and 0.2% more parameters compared to the baseline model, respectively. Meanwhile, they increase the number of MACs during inference by 0.2%, 1.6%, and 3.3%, respectively. According to Table VIII, the VGG extraction network in GeoEmbed introduces more parameters to the model. However, during inference, only the output features of VGG need to be recorded, as the input G(u, v) is fixed, introducing almost no additional complexity. Although the overall model complexity is higher, the main complexity comes from the baseline model. Finally, our SPDET has a similar computational complexity to NonLocal-DPT but shows significant improvements in both quantitative and visual aspects.

V. Limitations

In the previous sections, we have presented the successful cases of the proposed self-supervised panoramic depth estimation algorithm. However, based on experimental observations, the proposed SPDET performs poorly in outdoor scenes. Additionally, due to the lack of depth supervision, the depth prediction results still cannot match those of supervised methods.

A. Outdoor Scenes

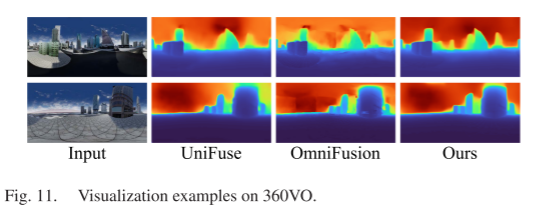
Indoor scenes capture contextual spatial structures with regular geometric layouts, guiding depth estimation for indoor panoramic images. Outdoor depth estimation typically focuses on driving scenarios, where panoramic cameras tend to capture sky areas and vehicles carrying the cameras, resulting in most content being ineffective for self-supervised depth estimation. Here, we use outdoor video sequences from 360VO for training and testing demonstrations.As shown in Figure 11, the sky and texture-less ground occupy most of the panoramic content, failing to provide the model with sufficient global structural information. Moreover, the extensive depth distribution range of the scene makes it challenging for the model to reconstruct fine depths. Nonetheless, our SPDET still reconstructs more complete and clearer depth maps than other models. Meanwhile, we observe noticeable stitching artifacts in the predictions of OmniFusion, indicating that its depth consistency optimization process requires sufficient depth constraints and fails in certain self-supervised scenarios.

B. Depth Supervision

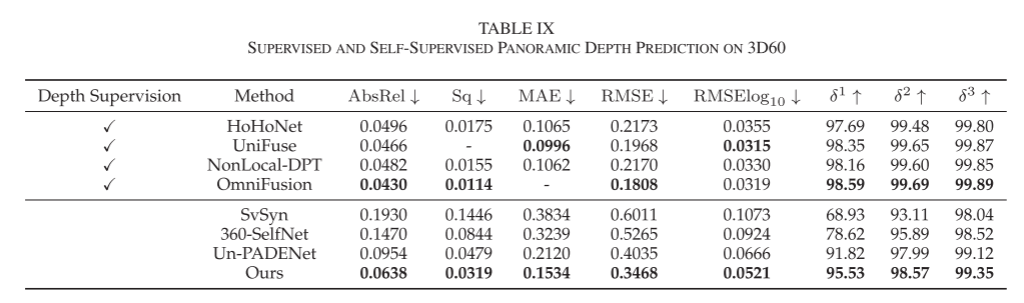
In this work, we proposed the SPDET method, optimizing multiple components of self-supervised monocular panoramic depth estimation processes and achieving state-of-the-art self-supervised performance. However, due to the lack of precise geometric supervision, the performance of self-supervised monocular depth estimation still lags far behind supervised models. We compare the results of state-of-the-art self-supervised and supervised algorithms on the 3D60 dataset in Table IX, following the depth evaluation metrics in previous supervised works without spherical weighting.As shown in Table IX, our SPDET significantly improves the accuracy of self-supervised depth estimation, exceeding the second place by 33.1% on the AbsRel metric and 27.6% on the MAE metric. However, SPDET still lags behind the state-of-the-art supervised work, falling short by 48.4% on the AbsRel metric and 54.0% on the MAE metric. Further narrowing the gap between supervised and self-supervised monocular panoramic depth estimation remains a key issue.

VI. Conclusion

In this work, we constructed SPDET, contributing to self-supervised panoramic depth estimation in several aspects. First, we proposed a panoramic transformer with spherical geometric features to predict the depth maps of panoramic images. To model the full spatial context of panoramic images, we embedded spherical geometric representations into the transformer through geometric embedding. We then designed a panoramic spatial pooling module to retain the global context extracted by the transformer and introduced an offset field resampling module for more effective feature upsampling in the convolutional decoder. During self-supervised training, we proposed pre-filtered DIBR to address the issue of occluded backgrounds mixing with foreground objects when synthesizing new views. Furthermore, we proposed an edge-aware loss function to tackle local optimum and over-smoothing problems in self-supervised depth estimation. Through the above improvements, we fully explore the potential of self-supervised monocular panoramic depth estimation and achieve state-of-the-art performance.It is worth noting that the camera poses used in our self-supervised training are known in the dataset rather than predicted by the network. Meanwhile, these synthetic datasets differ from real-world data as they do not contain invalid pixels violating camera motion and static scene assumptions. These real conditions will affect the performance of self-supervised depth estimation. We will discuss these issues in future work and refine the proposed self-supervised process to adapt to more practical scenarios.

Statement

The content of this article is a sharing of learning outcomes from the paper. Due to limitations in knowledge and ability, there may be deviations in understanding the original text, and the final content is subject to the original paper. The information in this article aims to disseminate and facilitate academic exchanges, and the content is the responsibility of the author, not representing the views of this account. If there are issues related to content, copyright, and others in the works mentioned in the text, please contact us in a timely manner, and we will respond and handle them as soon as possible.

Editor: PaperEveryDay