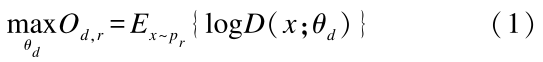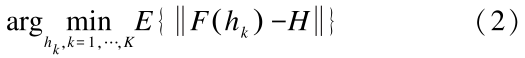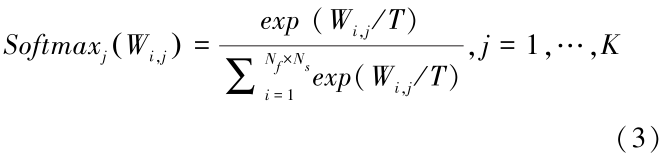Channel estimation is a fundamental issue in wireless communication systems, and its accuracy has a significant impact on applications such as signal recovery, interference management, and wireless resource allocation. Based on whether pilot signals are sent, channel estimation methods can be divided into three categories: blind channel estimation, pilot-based channel estimation, and semi-blind channel estimation. Among these, blind channel estimation is based on the statistical characteristics of the received signal, while pilot-based channel estimation obtains channel information by decoding the known pilot signals sent from the transmitter. To ensure high-accuracy channel estimation, the latter is widely applied.
With the emergence of numerous high-mobility and ultra-dense connection scenarios, a challenge faced by future 5G and 6G wireless communication systems is how to obtain high-accuracy channel estimation results[1]. Some researchers have suggested that the accuracy of channel estimation benefits from an increase in the number of pilots[2]. To ensure that the accuracy of channel estimation meets the demands of services, some traditional channel estimation methods such as least squares estimation and minimum mean square error estimation require an increase in the number of pilots. Additionally, both methods have their drawbacks[3]. Specifically, least squares estimation cannot be directly used to estimate the data channel, while minimum mean square error estimation requires first obtaining the correlation between the pilot channel and the data channel and also consumes additional computational resources for matrix inversion operations.
To overcome the aforementioned bottlenecks, the industry has researched some deep learning-based channel estimation methods. Depending on whether they incorporate traditional channel estimation methods, these deep learning-based methods can be divided into two categories: one designs neural network structures to serve as denoising modules and adds them to the traditional method workflow; the other applies neural network models to learn the correlation between the pilot channel and the data channel. However, although the above methods can achieve more accurate channel estimation results compared to traditional methods, their network structure design often heavily relies on specific pilot configuration schemes. This means that when the pilot configuration scheme changes, the model may need to be retrained, thus lacking support for flexible adaptive model deployment.
The Generative Adversarial Network (GAN) model, as an emerging neural network model, has demonstrated powerful data distribution learning capabilities in various fields[4], including image generation, image restoration, data augmentation, and communication networks[5]. In the field of wireless communications, GAN-based channel modeling schemes have sparked widespread research interest.
This paper proposes a GAN-based channel estimation method to support flexible channel estimation under any pilot configuration scheme and conducts performance verification in mid-to-high mobility scenarios in Orthogonal Frequency Division Multiplexing (OFDM) systems. Based on this, joint pilot configuration optimization is performed, and performance simulation verification results are provided.
1 Research on GAN-Based Channel Estimation Optimization Method
Existing channel estimation methods struggle to balance performance and pilot configuration flexibility. Specifically, traditional channel estimation methods do not rely on specific pilot configuration schemes, making them highly compatible but with poor performance; conversely, traditional Artificial Intelligence (AI) models depend on specific pilot configuration schemes, exhibiting strong performance but poor compatibility. Moreover, traditional AI models primarily validate scenarios with slow temporal changes in the channel at low speeds and have yet to perform performance validation in high-speed moving scenarios. Therefore, a new channel estimation method is needed to ensure that the estimation error achieves a low value under different pilot configuration schemes.
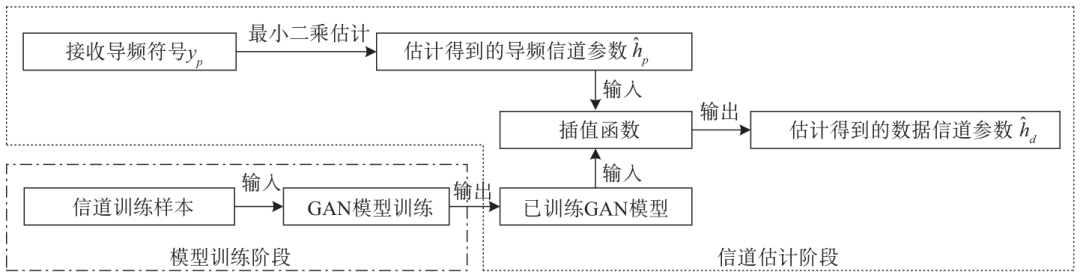
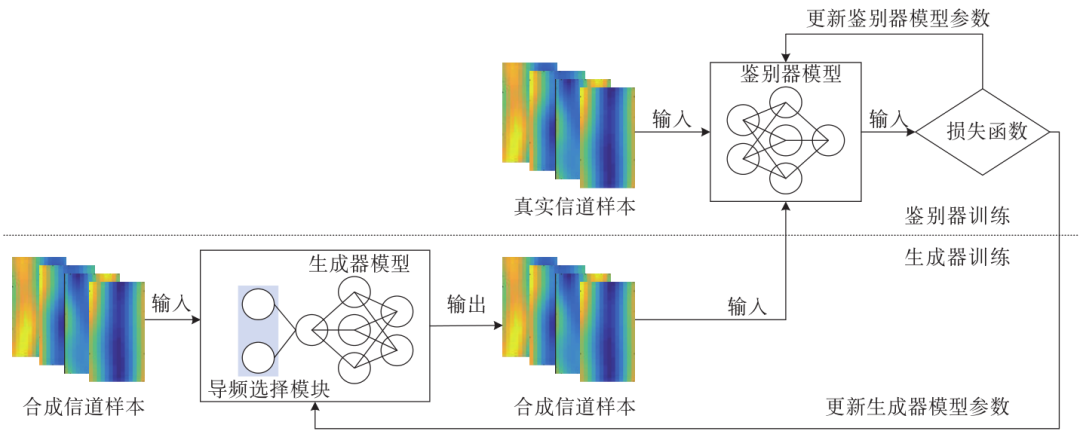
In light of this, this paper designs a GAN-based channel estimation method, with the overall process shown in Figure 1. The overall process consists of two stages: the model training stage and the model application stage. In the model training stage, the GAN model is used to train and generate synthetic channel samples that closely approximate the real channel sample distribution. Model training can be implemented online or offline. For offline training, previously collected channel data can be used to train the model, which is then deployed online for application. For online training, the model is trained based on real-time collected current channel data, enabling it to learn channel characteristics that better fit the current environment. Thus, the two training modes present a trade-off between deployment latency and the similarity of generated samples, allowing for the selection of an appropriate training mode based on different service requirements. Additionally, the joint application of both modes is also feasible, specifically by first training a model offline and then fine-tuning it online. In the model application stage, the estimated values of the current pilot channel are input into the trained model to obtain the estimated values of the data channel.
Figure 1 Flow of the GAN-Based Channel Estimation Method
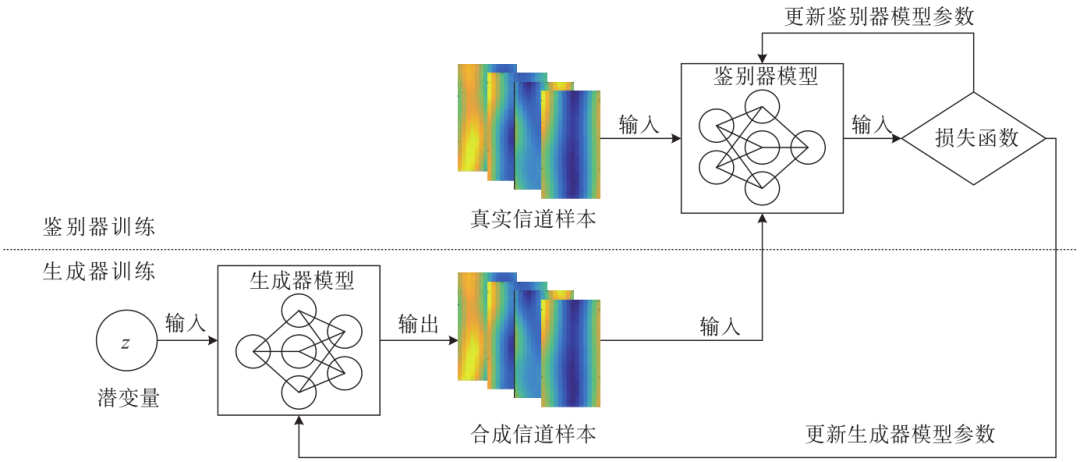
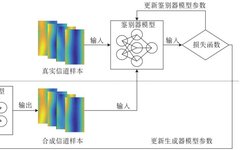
Figure 2 illustrates the training process of the GAN model. Depending on the type of data input into the discriminator model, the training process can be divided into two steps. When the input data consists of real samples, only the parameters of the discriminator model need to be updated. The training objective of the discriminator model is to classify the input real samples as true samples, maximizing the model’s output results, as shown in formula (1):
Figure 2 Schematic Diagram of the GAN Model Training Process
Where θd denotes the parameters of the discriminator model, D(·) indicates the output value of the discriminator model, and pr represents the distribution of real sample data.
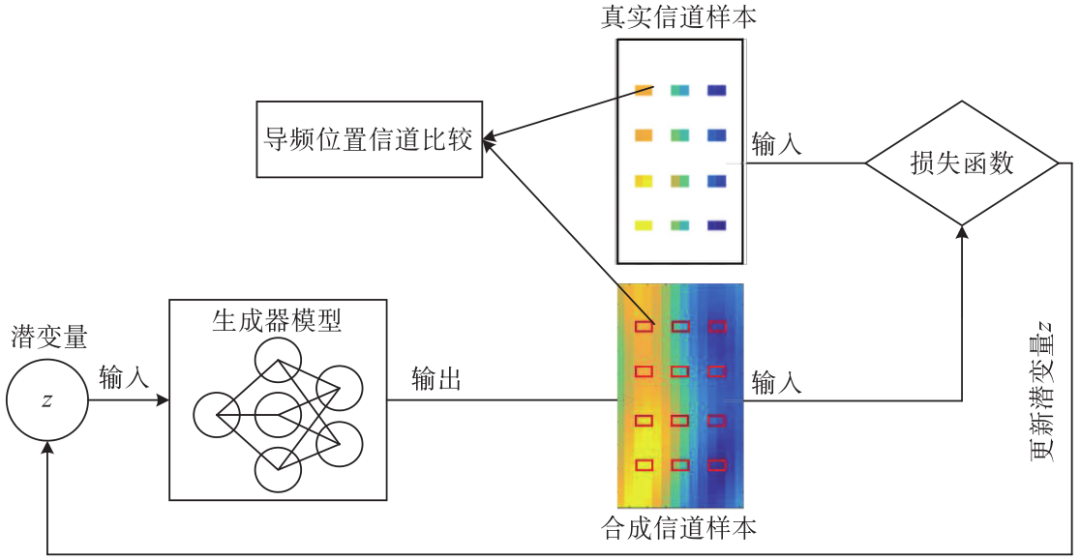
The channel estimation phase is essentially the process of recovering channel data. In this phase, the data channel information is estimated and restored using the known pilot channel and the trained GAN model. The channel restoration problem is similar to the image restoration problem in the field of computer vision[6]. Based on the generator’s ability to produce synthetic channel samples that follow the distribution of real channel samples, this problem can be effectively solved. Specifically, by continuously adjusting the latent variable z, the output of the generator can be altered to produce synthetic channel samples that closely approximate the channel information at known pilot locations. As shown in Figure 3, the channel information at known real pilot locations is compared with the synthetic channel samples initially generated randomly by the generator at corresponding pilot positions to calculate their difference. Subsequently, a gradient descent algorithm can be applied to update the value of z such that the synthetic channel samples output by the generator model approach the real pilot channel information at the pilot locations. When the number of iterations reaches a certain threshold, the difference between the two is minimized, allowing the optimal solution for the reconstructed channel sample z* to be obtained. The z* is then input into the generator model to acquire the data channel information.
Figure 3 Process of Using the Generator Model to Recover the Data Channel
2 Joint Optimization Algorithm for Pilot Configuration and Channel Estimation Based on GAN
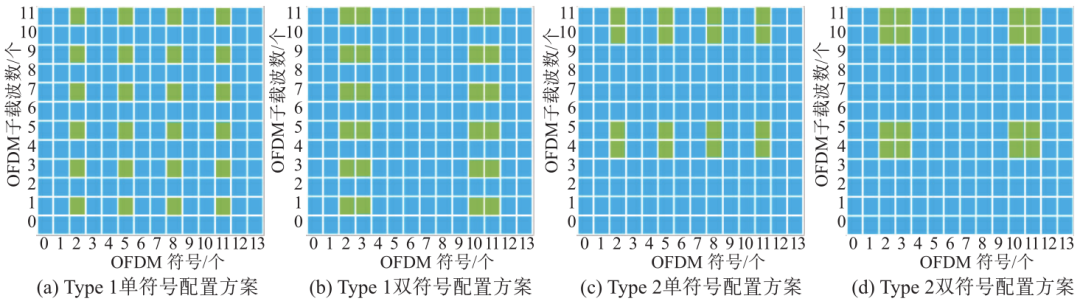
As shown in Figure 4, the existing 3GPP TS 38.211 standard[7] specifies pilot configuration schemes, with candidate configuration types including Type 1 and Type 2. These two types of configurations are distinguished by the insertion density of pilots in the frequency domain. For Type 1 configuration, pilots are distributed at intervals in the frequency domain, with an insertion density of 50%; whereas for Type 2 configuration, adjacent pairs of subcarriers constitute a group, with a group inserted every four subcarriers, resulting in an insertion density of 33%[7]. Additionally, from the perspective of the time domain of OFDM symbols, there are also single-symbol and double-symbol configuration schemes. Specifically, in terms of columns, the single-symbol configuration can be expanded to a maximum of four columns as needed, with the single-symbol configuration schemes for Type 1 and Type 2 illustrated in Figures 4(a) and 4(c) respectively; while the double-symbol configuration consists of adjacent pairs of columns grouped together, which can be expanded to a maximum of two groups as needed, with the double-symbol configuration schemes for Type 1 and Type 2 illustrated in Figures 4(b) and 4(d) respectively.
Figure 4 Pilot Configuration Schemes
The base station can select an appropriate configuration scheme based on scheduling needs, greatly simplifying the process and complexity of configuring pilot signals, but at the cost of sacrificing potential air interface transmission performance. It should be noted that for any dataset composed of OFDM frames, the amount of information contained in each resource block is different. Therefore, whether the pilot set specified by the standard adequately characterizes the resource block set with the maximum information capacity remains uncertain, thus making it questionable whether the full OFDM frame channel can be reconstructed most accurately using this pilot set. Furthermore, for different channel environments, the information capacity contained in each resource block may change, leading to alterations in the optimal pilot set. In summary, existing pilot configuration schemes do not provide support for adaptive optimization of pilot configurations tailored to specific channel environments, limiting the in-depth exploration and release of potential channel estimation performance.
To address the pilot position configuration optimization problem, a model can be established under the condition of a given number of pilots K, seeking K resource blocks containing the maximum information capacity within an Nf × Ns dimensional space, such that the complete OFDM channel matrix can be reconstructed with minimal error through the channel information from these K resource blocks, as expressed in formula (2):
Where hk,k=1,…,K represents the selected pilot set, F denotes the channel reconstruction function, then F(hk) indicates the reconstructed channel matrix, and H represents the complete OFDM channel matrix.
Considering that there are C possible candidate solutions for the problem under study, which exhibit explosive growth with the increase in channel scale, the simplest traversal algorithm is not applicable. Furthermore, due to the limited ability of traditional methods to characterize the correlation between time-frequency resource blocks, this subsection proposes a solution based on AI models.
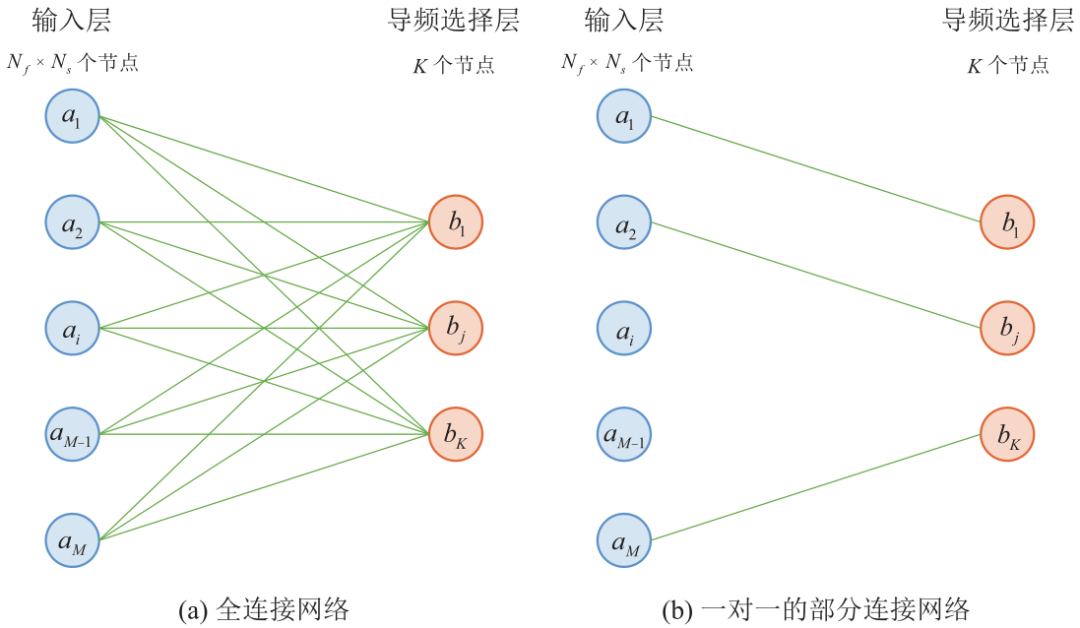
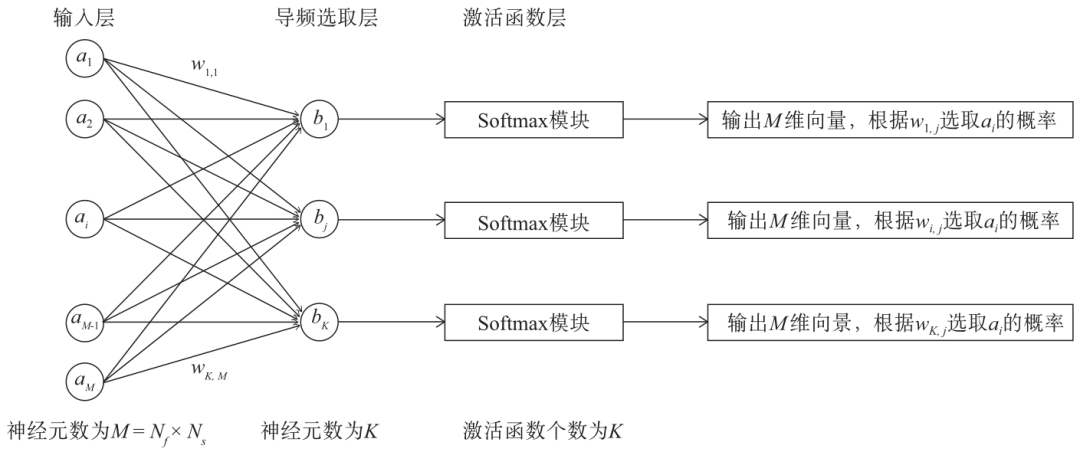
Based on the concept and ideas presented by Abid[8] et al. concerning neuron selection layers, this subsection will add this module to the previously mentioned GAN model, enabling it to optimize pilot selection. Below, the basic idea of the neuron selection layer is introduced. Figure 5 shows the structure of a two-layer linear network model, where the number of neurons in the first layer is set to Nf ×Ns, corresponding to the total number of resource blocks in a single OFDM frame, while the number of neurons in the second layer is set to K, corresponding to the number of pilots to be selected. As shown in Figure 5(a), at the initial state of training, the two layers of neurons are fully connected, indicating that each resource block has an equal probability of being selected. Through continuous training of the model, if the probability of selecting certain resource blocks with high information capacity can be increased, the final convergence effect of the model will be as shown in Figure 5(b), where some neurons in the first layer are one-to-one connected with neurons in the second layer, thereby optimizing pilot selection.
Figure 5 Structure of Two-Layer Linear Network Model
By connecting a temperature-controlled Softmax function module after each neuron in the second layer, the aforementioned goal can be achieved. The temperature-controlled Softmax function is an improvement over the original Softmax function, incorporating a “simulated annealing” mechanism, as shown in formula (3):
 Figure 6 Structure of the Neuron Selection Layer
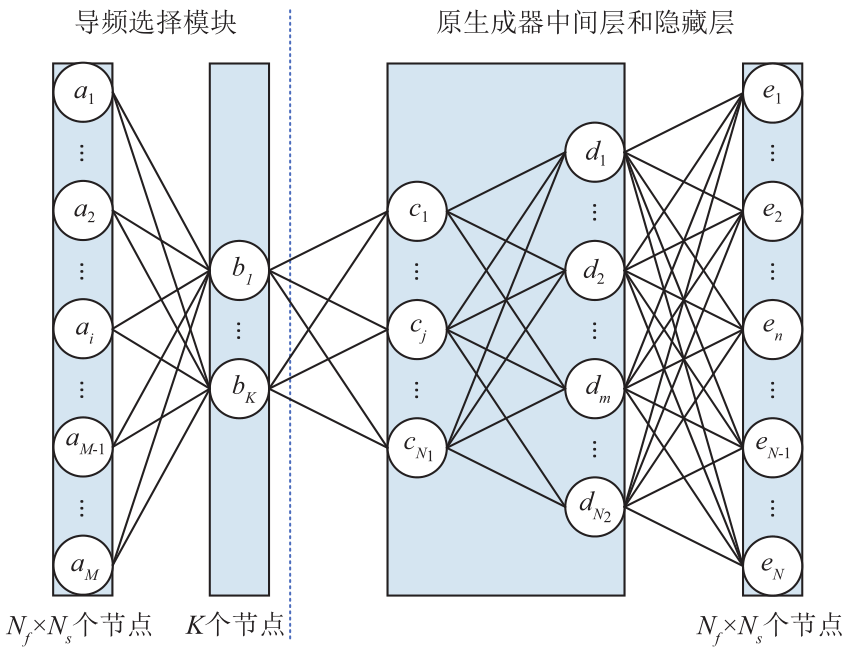
By combining the pilot selection module’s neuron selection layer with the aforementioned GAN model, the joint design of pilot patterns and channel estimation can be achieved, with the specific structure illustrated in Figure 7. The core of this joint design scheme is to cascade the pilot selection module with the generator network. Since the pilot selection module selects information-rich resource blocks as pilots from the complete dimensionality of channel resource blocks, the input to the generator network is changed from the original low-dimensional Gaussian random vector to real channel samples. Consequently, the cascaded generator network’s model structure changes to that shown in Figure 8, where the first layer of the pilot selection module contains Nf ×Ns neurons, the second layer contains K neurons, and the subsequent layers maintain the same model structure as the previous model. The structure of the discriminator network remains unchanged.
Figure 7 Training Block Diagram of the Joint Design Model for Pilot Configuration and Channel Estimation Based on GAN
Figure 8 Structure of the Generator Model with the Cascaded Pilot Selection Module
During the training process of the cascaded generator model, it is necessary to continuously reduce the temperature, gradually converging the search space of solutions from the initial candidate pool of dimension C to a smaller range. Additionally, the loss function serves to characterize the degree of difference between the complete channel reconstructed based on the selected resource blocks and the real complete channel. Through continuous updates of the model parameters, this degree of difference can be minimized.
3 Simulation Settings and Result Analysis
In the simulation validation, the channel dataset contains 20,000 channel samples, all generated based on the Tapped Delay Line Type C (TDL-C) model[9]. In this paper, the training set data accounts for 80% of the total data volume. All data samples have undergone power normalization. The number of subcarriers and symbols in the OFDM block is set to Nf = 48 and Ns = 14, respectively. The carrier frequency is set to f=3.5 GHz, with each subcarrier’s bandwidth set to Bf =30 kHz, and the total transmission time of each OFDM block is T=0.5 ms. To avoid inter-symbol interference, a cyclic prefix accounting for 6% of the total symbol length is added before each symbol. Furthermore, to ensure that the maximum transmission delay of multipath does not exceed the duration of the cyclic prefix, the root mean square delay spread is set to Td=300 ns. The optimization results for different pilot counts in scenarios with speeds of 150 km/h and 300 km/h are provided, validating the performance gains of the proposed method. The newly added simulation parameter settings are as follows: the initial temperature and cooling temperature are set to T0=10 and TE=0.05.
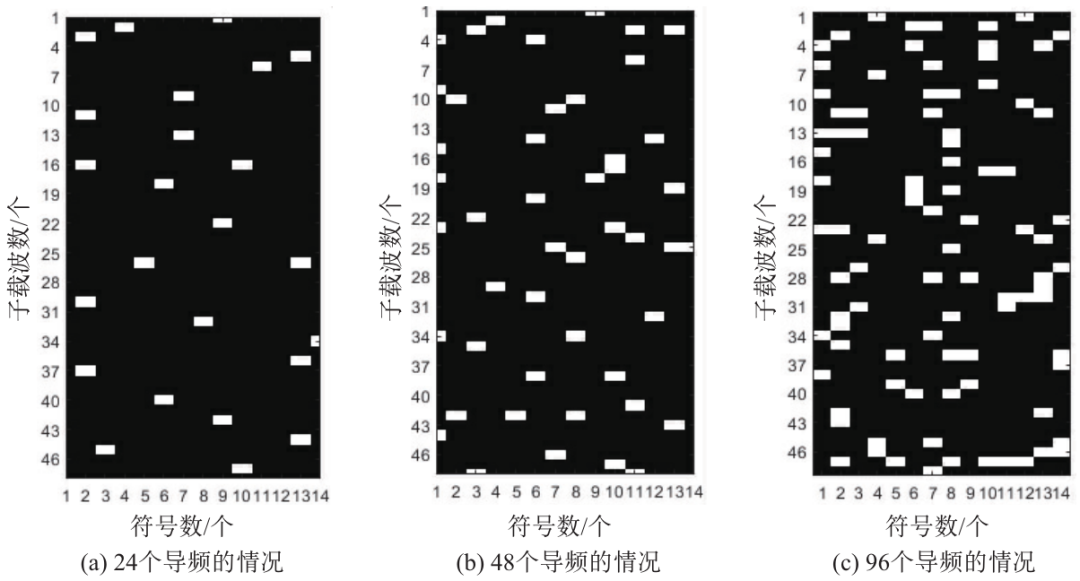
Figure 9 Optimization Results of Pilot Selection in 150 km/h Speed Scenario
Figure 10 Optimization Results of Pilot Selection in 300 km/h Speed Scenario
To quantitatively assess the performance of the joint optimization scheme for pilot configuration and channel estimation based on GAN proposed in this subsection, this paper uses Normalized Mean Squared Error (NMSE) as the evaluation index, comparing it with the classic two-dimensional Wiener filtering interpolation algorithm and the GAN channel estimation method without pilot optimization. Table 1 shows the evaluation results for the two speed scenarios with a signal-to-noise ratio of 20 dB. As shown in Table 1, compared to the GAN scheme without optimized pilot configuration, the joint optimization scheme can further improve channel estimation performance. Specifically, for both speed scenarios, the performance of the joint optimization scheme using only 24 pilots is equivalent to that of the GAN scheme with 96 pilots under unoptimized pilot configuration, indicating that the joint optimization scheme can reduce pilot overhead by 75% with almost no performance loss. Furthermore, when the pilot overhead of both schemes is the same, for the 150 km/h speed scenario, the performance of the joint optimization scheme can be improved by approximately 1.7 dB; while for the 300 km/h speed scenario, the performance enhancement can reach about 2.1 dB.
Table 1 Simulation Performance Evaluation of the Joint Optimization Scheme at a Signal-to-Noise Ratio of 20 dB
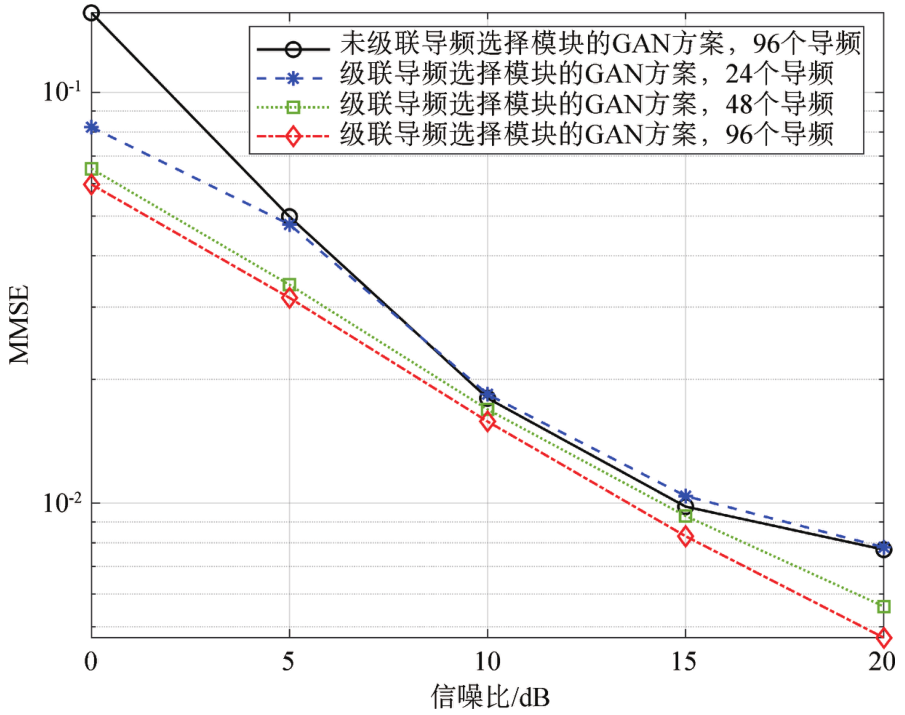
Figure 11 shows the NMSE performance curves of the joint optimization scheme under different signal-to-noise ratio conditions in the 300 km/h speed scenario. The GAN channel estimation method without pilot configuration optimization is used as a comparison scheme. As seen in Figure 11, under the application of 24 pilots, the performance of the joint optimization scheme is comparable to that of the GAN channel estimation method without pilot configuration optimization over a signal-to-noise ratio range of 5-20 dB. When the signal-to-noise ratio is lower, the performance of the joint optimization scheme is better, indicating that the joint optimization scheme possesses certain anti-noise capabilities. Moreover, with more pilots supported, the joint optimization scheme exhibits outstanding NMSE performance across the 0-20 dB signal-to-noise ratio range.
Figure 11 Performance Evaluation of the Joint Optimization Scheme in the 300 km/h Speed Scenario
In the future, human society will enter an intelligent era, and 6G will construct a ubiquitous interconnected intelligent network, realizing the beautiful vision of serving humans, interconnecting people and things, and achieving smart connections among thousands of households and all things. The deep integration of wireless communication and artificial intelligence is expected to promote the evolution of future communication paradigms and innovation in network architecture, providing support for the realization of the intelligent development vision in the 6G era. To fully utilize the rich data distributed at the network edge for the training of artificial intelligence models, edge intelligence technologies represented by federated edge learning have emerged. This paper focuses on channel estimation in wireless communication, conducting research on GAN-based channel estimation methods, and verifying the feasibility of the proposed algorithm through simulation results.
Assistant Engineer at the Mobile Communication Innovation Center of the China Academy of Information and Communications Technology, primarily researching wireless artificial intelligence for 6G.
Engineer at the Mobile Communication Innovation Center of the China Academy of Information and Communications Technology, primarily researching new generation mobile communication and artificial intelligence convergence technologies.
Senior Engineer at the Mobile Communication Innovation Center of the China Academy of Information and Communications Technology, primarily researching wireless artificial intelligence and integrated communication sensing technologies for 6G.
Senior Engineer at the Mobile Communication Innovation Center of the China Academy of Information and Communications Technology, primarily researching 6G wireless air interface technologies and ITU international standards.
Senior Engineer at the Mobile Communication Innovation Center of the China Academy of Information and Communications Technology, primarily researching wireless artificial intelligence and integrated communication sensing technologies for 6G.
Figure 6 Structure of the Neuron Selection Layer
By combining the pilot selection module’s neuron selection layer with the aforementioned GAN model, the joint design of pilot patterns and channel estimation can be achieved, with the specific structure illustrated in Figure 7. The core of this joint design scheme is to cascade the pilot selection module with the generator network. Since the pilot selection module selects information-rich resource blocks as pilots from the complete dimensionality of channel resource blocks, the input to the generator network is changed from the original low-dimensional Gaussian random vector to real channel samples. Consequently, the cascaded generator network’s model structure changes to that shown in Figure 8, where the first layer of the pilot selection module contains Nf ×Ns neurons, the second layer contains K neurons, and the subsequent layers maintain the same model structure as the previous model. The structure of the discriminator network remains unchanged.
Figure 7 Training Block Diagram of the Joint Design Model for Pilot Configuration and Channel Estimation Based on GAN
Figure 8 Structure of the Generator Model with the Cascaded Pilot Selection Module
During the training process of the cascaded generator model, it is necessary to continuously reduce the temperature, gradually converging the search space of solutions from the initial candidate pool of dimension C to a smaller range. Additionally, the loss function serves to characterize the degree of difference between the complete channel reconstructed based on the selected resource blocks and the real complete channel. Through continuous updates of the model parameters, this degree of difference can be minimized.
3 Simulation Settings and Result Analysis
In the simulation validation, the channel dataset contains 20,000 channel samples, all generated based on the Tapped Delay Line Type C (TDL-C) model[9]. In this paper, the training set data accounts for 80% of the total data volume. All data samples have undergone power normalization. The number of subcarriers and symbols in the OFDM block is set to Nf = 48 and Ns = 14, respectively. The carrier frequency is set to f=3.5 GHz, with each subcarrier’s bandwidth set to Bf =30 kHz, and the total transmission time of each OFDM block is T=0.5 ms. To avoid inter-symbol interference, a cyclic prefix accounting for 6% of the total symbol length is added before each symbol. Furthermore, to ensure that the maximum transmission delay of multipath does not exceed the duration of the cyclic prefix, the root mean square delay spread is set to Td=300 ns. The optimization results for different pilot counts in scenarios with speeds of 150 km/h and 300 km/h are provided, validating the performance gains of the proposed method. The newly added simulation parameter settings are as follows: the initial temperature and cooling temperature are set to T0=10 and TE=0.05.
Figure 9 Optimization Results of Pilot Selection in 150 km/h Speed Scenario
Figure 10 Optimization Results of Pilot Selection in 300 km/h Speed Scenario
To quantitatively assess the performance of the joint optimization scheme for pilot configuration and channel estimation based on GAN proposed in this subsection, this paper uses Normalized Mean Squared Error (NMSE) as the evaluation index, comparing it with the classic two-dimensional Wiener filtering interpolation algorithm and the GAN channel estimation method without pilot optimization. Table 1 shows the evaluation results for the two speed scenarios with a signal-to-noise ratio of 20 dB. As shown in Table 1, compared to the GAN scheme without optimized pilot configuration, the joint optimization scheme can further improve channel estimation performance. Specifically, for both speed scenarios, the performance of the joint optimization scheme using only 24 pilots is equivalent to that of the GAN scheme with 96 pilots under unoptimized pilot configuration, indicating that the joint optimization scheme can reduce pilot overhead by 75% with almost no performance loss. Furthermore, when the pilot overhead of both schemes is the same, for the 150 km/h speed scenario, the performance of the joint optimization scheme can be improved by approximately 1.7 dB; while for the 300 km/h speed scenario, the performance enhancement can reach about 2.1 dB.
Table 1 Simulation Performance Evaluation of the Joint Optimization Scheme at a Signal-to-Noise Ratio of 20 dB
Figure 11 shows the NMSE performance curves of the joint optimization scheme under different signal-to-noise ratio conditions in the 300 km/h speed scenario. The GAN channel estimation method without pilot configuration optimization is used as a comparison scheme. As seen in Figure 11, under the application of 24 pilots, the performance of the joint optimization scheme is comparable to that of the GAN channel estimation method without pilot configuration optimization over a signal-to-noise ratio range of 5-20 dB. When the signal-to-noise ratio is lower, the performance of the joint optimization scheme is better, indicating that the joint optimization scheme possesses certain anti-noise capabilities. Moreover, with more pilots supported, the joint optimization scheme exhibits outstanding NMSE performance across the 0-20 dB signal-to-noise ratio range.
Figure 11 Performance Evaluation of the Joint Optimization Scheme in the 300 km/h Speed Scenario
In the future, human society will enter an intelligent era, and 6G will construct a ubiquitous interconnected intelligent network, realizing the beautiful vision of serving humans, interconnecting people and things, and achieving smart connections among thousands of households and all things. The deep integration of wireless communication and artificial intelligence is expected to promote the evolution of future communication paradigms and innovation in network architecture, providing support for the realization of the intelligent development vision in the 6G era. To fully utilize the rich data distributed at the network edge for the training of artificial intelligence models, edge intelligence technologies represented by federated edge learning have emerged. This paper focuses on channel estimation in wireless communication, conducting research on GAN-based channel estimation methods, and verifying the feasibility of the proposed algorithm through simulation results.
Assistant Engineer at the Mobile Communication Innovation Center of the China Academy of Information and Communications Technology, primarily researching wireless artificial intelligence for 6G.
Engineer at the Mobile Communication Innovation Center of the China Academy of Information and Communications Technology, primarily researching new generation mobile communication and artificial intelligence convergence technologies.
Senior Engineer at the Mobile Communication Innovation Center of the China Academy of Information and Communications Technology, primarily researching wireless artificial intelligence and integrated communication sensing technologies for 6G.
Senior Engineer at the Mobile Communication Innovation Center of the China Academy of Information and Communications Technology, primarily researching 6G wireless air interface technologies and ITU international standards.
Senior Engineer at the Mobile Communication Innovation Center of the China Academy of Information and Communications Technology, primarily researching wireless artificial intelligence and integrated communication sensing technologies for 6G.
Citation Format:
XU Mingfeng, LI Yang, HAN Kaifeng, et al. Joint Optimization Algorithm for Pilot Configuration and Channel Estimation Based on GAN[J]. Information Communication Technology and Policy, 2023, 49(9): 58-66.
This paper was published in “Information Communication Technology and Policy” 2023, Issue 9
Organized by: China Academy of Information and Communications Technology
“Information Communication Technology and Policy” is a professional academic journal sponsored by the Ministry of Industry and Information Technology and organized by the China Academy of Information and Communications Technology. This journal positions itself as a barometer of cutting-edge information communication technology trends and a think tank for exploring information society policies, focusing on technology trends, public policies, national/industry/enterprise strategies in the information communication field, and publishing cutting-edge research results, analysis of key issues, and interpretation of hot policies, promoting the innovation and development of technologies and industries such as 5G, industrial internet, digital economy, artificial intelligence, blockchain, big data, and cloud computing, guiding national technology strategy choices and industrial policy formulation, and building a high-end academic exchange platform for production, learning, research, and application.
Submission Guidelines for “Information Communication Technology and Policy”!
To further improve the level of journal informatization and provide better services to scholars, the official website of our journal has been officially launched, and submissions are welcome!
Proofread by | Jin Yan, Shan Shan
Edited by | Ling Xiao
China Academy of Information and Communications Technology, Du Liutong et al.: Global Development Trends of 6G Technology Industry